AVL树

搜索二叉树左右高度会差很多，会导致查找时间复杂度变差，所以就有了AVL树。

AVL树：左右子树都是AVL树，左右子树的高度差不超过1.

平衡因子 = 右子树高度-左子树高度。

AVL树是二叉搜索树的进阶。只是需要引入平衡因子。

右单旋：左边高右边低。

抽象图如下所示：

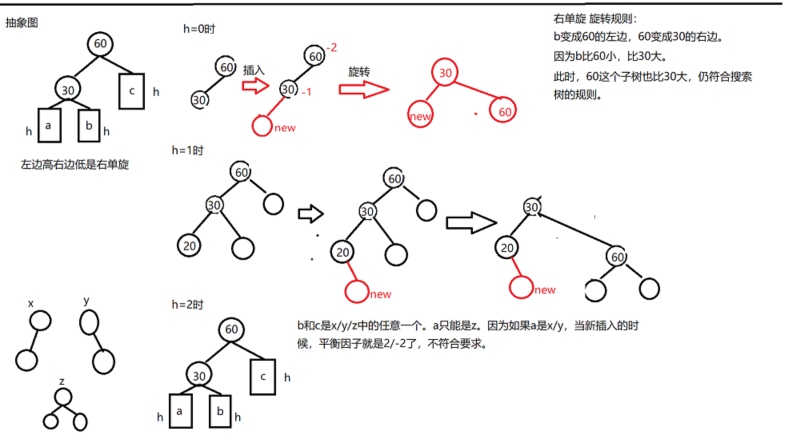
右单旋的过程如下所示：

代码如下：

void RotateR(Node* parent)
{Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR){SubLR->_parent = parent;}SubL->_right = parent;Node* pparent = parent->_parent;//如果parent不是root,所以需要父亲的父亲，为什么在这里定义，因为下一行代码parent已经更新了parent->_parent = SubL;if (parent == _root){_root = SubL;_root->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = SubL;}else{pparent->_right = SubL;}SubL->_parent = pparent;}parent->_bf = SubL->_bf = 0;
}

左单旋：右高左低。

旋转过程：

左旋转代码如下：

//左单旋
void RotateL(Node* parent)
{Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}SubR->_left = parent;Node* pparent = parent->_parent;//如果parent不是root,所以需要父亲的父亲，为什么在这里定义，因为下一行代码parent已经更新了parent->_parent = SubR;if (parent == _root){_root = SubR;_root->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = SubR;}else{pparent->_right = SubR;}SubR->_parent = pparent;}parent->_bf = SubL->_bf = 0;
}

上面的左单旋和右单旋指的是一边高就旋转，而不是像折线那样比较高度。

 

 左右双旋分两种情况：

实现代码如下：

//左右双旋,旋转之后平衡因子也要变化。
void RotateLR(Node* parent)
{Node* SubL = parent->_left;Node* SubLR = SubL->_right;int bf = SubLR->_bf;RotateL(parent->_left);//左旋RotateR(parent);//右旋if (bf == -1)//在b插入节点{SubLR->_bf = 0;SubL->_bf = 0;parent->_bf = -1;}else if (bf == 1)//在c插入节点{SubLR->_bf = 0;parent->_bf = 0;SubL->_bf = 0;}else{assert(false);}
}

右左双旋：

代码如下：

//右左双旋
void RotateRL(Node* parent)
{Node* SubR = parent->_right;Node* SubRL = SubL->_left;int bf = SubRL->_bf;RotateL(parent->_right);//右旋RotateR(parent);//左旋SubRL->_bf = 0;if (bf == -1)//在e插入节点{SubR->_bf = 1;parent->_bf = 0;}else if (bf == 1)//在f插入节点{subR->_bf = 0;parent->_bf = -1;}else{parent->_bf = 0;subR->_bf = 0;}
}

整体代码如下所示：

#pragma oncetemplate<class k,class v>//定义树的节点
struct AvlTreeNode
{AvlTreeNode<k, v>* _left;AvlTreeNode<k, v>* _right;AvlTreeNode<k, v>* _parent;pair<k, v> _kv;int _bf;//平衡因子AvlTreeNode(const pair<k,v>& kv):_left(nullptr)  ,_right(nullptr)   ,_parent(nullptr)   ,_kv(kv)  ,_bf(0)  { }
};template<class k,class v>
class AvlTree
{typedef AvlTreeNode<k, v> Node;
public:bool Insert(const pair<k, v>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if(cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//插入新节点//插入之后需要更新平衡因子while (parent){if (cur == parent->_left) //如果插入在左边，左高右低。父亲的平衡因子-1{parent->_bf--;}else //插入在右边，右高左低。父亲的平衡因子+1{parent->_bf++;}if (parent->_bf == 0)//父亲的平衡因子==0说明已经平衡了{break;}else if (parent->_bf == 1 || parent->_bf == -1)//继续向上更新,parent和cur进行更新{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//当前子树不平衡了，需要旋转处理平衡问题{if (parent->_bf == -2 && cur->_bf == -1)//左边高{RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1)//右边高{RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1)//折现-右高左高，需要双旋{RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1)//左高右高，需要双旋{RotateLR(parent);}break;}else{// 理论而言不可能出现这个情况assert(false);}}return true;}//右单旋void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR){SubLR->_parent = parent;}SubL->_right = parent;Node* pparent = parent->_parent;//如果parent不是root,所以需要父亲的父亲，为什么在这里定义，因为下一行代码parent已经更新了parent->_parent = SubL;if (parent == _root){_root = SubL;_root->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = SubL;}else{pparent->_right = SubL;}SubL->_parent = pparent;}parent->_bf = SubL->_bf = 0;}//左单旋void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;parent->_right = SubRL;if (SubRL){SubRL->_parent = parent;}SubR->_left = parent;Node* pparent = parent->_parent;//如果parent不是root,所以需要父亲的父亲，为什么在这里定义，因为下一行代码parent已经更新了parent->_parent = SubR;if (parent == _root){_root = SubR;_root->_parent = nullptr;}else{if (parent == pparent->_left){pparent->_left = SubR;}else{pparent->_right = SubR;}SubR->_parent = pparent;}parent->_bf = SubL->_bf = 0;}//左右双旋,旋转之后平衡因子也要变化。void RotateLR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;int bf = SubLR->_bf;RotateL(parent->_left);//左旋RotateR(parent);//右旋if (bf == -1)//在b插入节点{SubLR->_bf = 0;SubL->_bf = 0;parent->_bf = -1;}else if (bf == 1)//在c插入节点{SubLR->_bf = 0;parent->_bf = 0;SubL->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}//右左双旋void RotateRL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubL->_left;int bf = SubRL->_bf;RotateL(parent->_right);//右旋RotateR(parent);//左旋SubRL->_bf = 0;if (bf == -1)//在e插入节点{SubR->_bf = 1;parent->_bf = 0;}else if (bf == 1)//在f插入节点{subR->_bf = 0;parent->_bf = -1;}else{parent->_bf = 0;subR->_bf = 0;}}
private:Node* _root;
};