计算机图形学:(四)欧拉角与四元数
# 导语
在计算机图形学的学习中,几何变换(Transformations)是一块重要的内容,我们使用齐次坐标描述点和向量,使用变换矩阵描述平移、旋转等变换。而在平移、旋转、缩放这几种变换中,又以旋转的情况最为复杂。实际上,计算机图形学中三维空间的旋转不仅仅有旋转矩阵一种表达形式,欧拉角(Euler angles)和四元数(Quaternions)也是常用的方法。
# 旋转矩阵
这里再复习一下在计算机图形学:(一)基础中提到的旋转矩阵,假设绕XYZ三个轴旋转的角度分别为 α,β,γ ,则这三次旋转的旋转矩阵计算方法如下:

最终的旋转矩阵为:

# 欧拉角
旋转矩阵表面上看起来依赖于 9 个参数,实际上只有三个是独立的。为了更直接地指出这三个独立参数,欧拉(Euler)证明了如下事实:任何一个旋转都可以由连续施行的三次绕轴旋转来实现,这三次绕轴旋转的旋转角(α,β,γ )就是三个独立参数,称为欧拉角。

欧拉角,这一数学概念,是描述物体在三维空间中绕坐标系三个轴(x, y, z轴)的旋转角度。它将方位(角位移)分解为绕这三个互相垂直轴的旋转,且这种分解具有任意性,即任意三个轴和旋转顺序都可以组成一个有效的欧拉角。

🎈注:不同软件/引擎的默认坐标系不同,Heading(Yaw)通常指绕垂直轴的旋转(即取决于坐标系是Y-up还是Z-up)。如在Z-up系统中,heading-pitch-roll即为绕ZYX旋转;在GLM库中,eulerAngleYXZ()函数与yawPitchRoll()函数结果一致 [链接]。
不同的旋转顺序会导致旋转结果不同,因此需要按照特定的旋转顺序进行欧拉角的计算和使用。在不考虑使用两种不同的约定来定义旋转(内旋或外旋,注:在后文再提及)的可能性下,存在12种可能得旋转轴序列,分为两组:
(一)Proper Euler angles:也称为真欧拉角或者经典欧拉角。经典欧拉角中第一旋转轴和第三旋转轴是相同的,共有6种可能序列:

(二)Tait–Bryan angles:也称为泰特-布莱恩角,万向角,航海角度,或者直接描述三个角(航向,海拔和高度或者偏航,俯仰和滚动) 。泰特-布莱恩角中三个角分别绕三个不同的轴转动,共有6种可能得序列:

在实际使用中,为了简单起见,广泛采用“heading-pitch-roll”约定(注:heading有时也用yaw表示),它让物体从“标准”方位开始旋转,即物体坐标轴与惯性坐标系原点对齐。这种旋转顺序能通过依次作heading、pitch和roll旋转,使物体到达我们想要描述的方位。
欧拉角可分为两种情况:①静态欧拉角(又称为外旋欧拉角)和②动态欧拉角(又称为内旋欧拉角)。
-
静态欧拉角
静态欧拉角是指物体绕世界坐标系三个轴的旋转,在这种情况下物体坐标轴保持静止。
若按X-Y-Z旋转顺序(指先绕固定轴X,再绕固定轴Y,最后绕固定轴Z),可得旋转矩阵:
![]()
-
动态欧拉角
动态欧拉角则是指物体在自身坐标系中的旋转,这种旋转的复杂之处在于其坐标轴会随物体一起转动。
若按Z-Y-X旋转顺序(指先绕自身轴Z,再绕自身轴Y,最后绕自身轴X),可得旋转矩阵:
![]()
看到这里时泛起了迷糊,其他教程里以一句“外旋是左乘,内旋是右乘”草草带过,那么为什么是这样呢?
这里来推导一下。首先,因为已经假设了物体自身轴对齐世界轴,所以绕物体X轴等价于绕世界的X旋转。若旋转顺序是XYZ,绕自身Y旋转的时候,已经存在X旋转了,已经被X轴的旋转影响到了。那么为了得到绕Y的旋转矩阵,我们先撤销绕自身X轴的旋转,进行Y旋转,再恢复X轴旋转。同理,为了得到绕Z的旋转矩阵,需要撤销Y轴旋转,再撤销X轴旋转,再进行Z轴旋转,再恢复X、Y轴旋转 [链接]。

则内旋转最终表示为:
![]()
那么若旋转顺序是ZYX,同理可得到:
![]()
明白这点后,回到推导前,可以看到。这个结论说明Z-Y-X顺序的内旋等价于X-Y-Z顺序的外旋。任何的外旋都等于角度相同但元素旋转顺序相反的内旋,反之亦然。
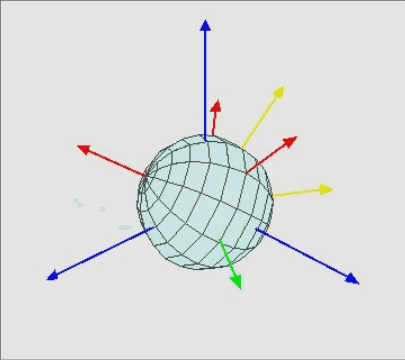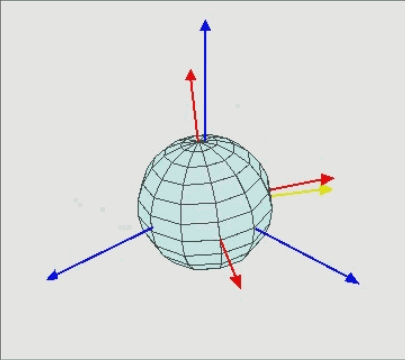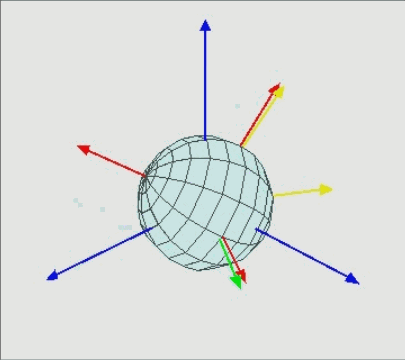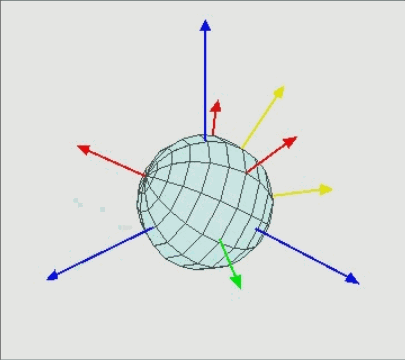
用图片演示一下,最终下面两图表示了相同的旋转结果:


内旋动画版(① 物体绕轴旋转 α 角度, 旋转后得到
;② 物体绕
轴旋转 β 角度,旋转后得到
;③ 物体绕
轴旋转 γ 角度,旋转后得到
):
# 万向节锁(Gimbal Lock)
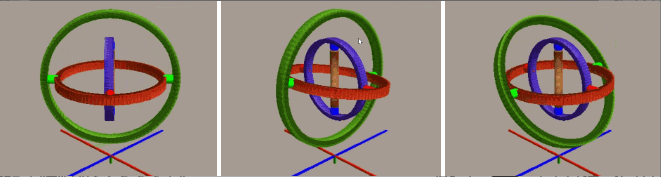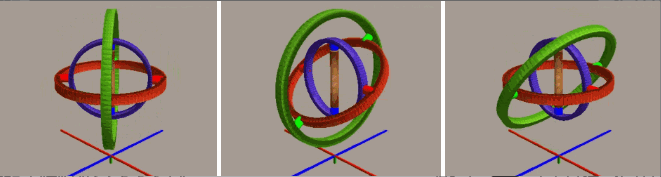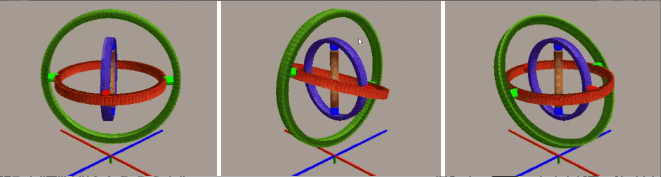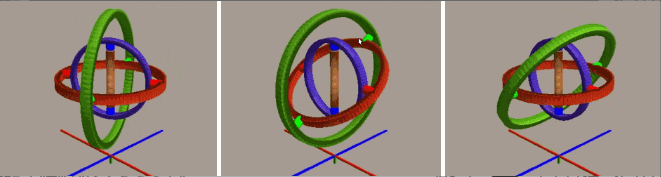
通过欧拉角我们可以直观地理解物体的旋转,但其缺点在于可能面临万向锁问题。我们使用平衡环来动态演示该问题:

一开始承载物体的三个环互相垂直,构成直角坐标系,如将位于中间的红环旋转 90 度(顺/逆时针),就会发现最内侧的蓝环就会和最外侧的绿环环处于同一个平面上(即物体的两个旋转轴指向了同一个方向),导致整个系统丢失了一个“自由度”,也就是说现在内外侧的环对于物体施加的旋转效果是等效的。
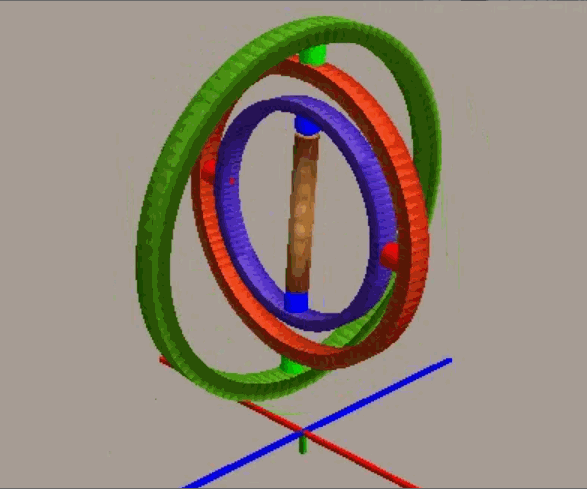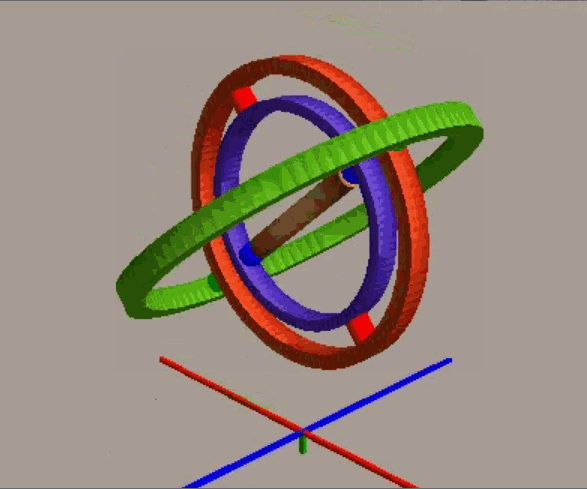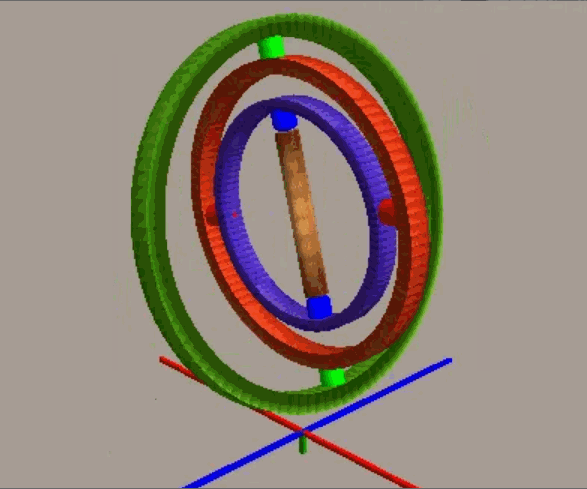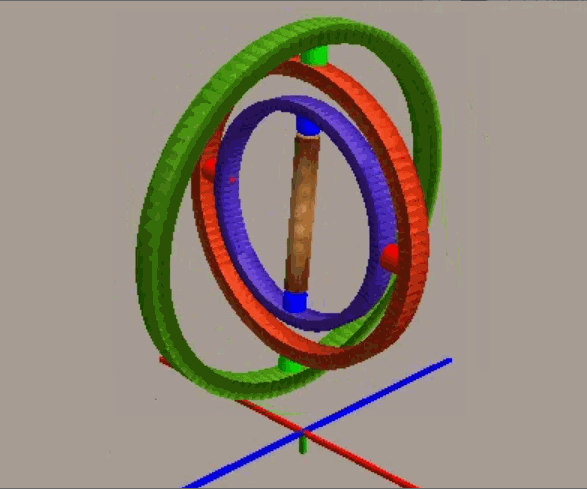
从代数意义来看,对于zyx轴顺序的旋转(内旋),按β=±90°,代入矩阵计算:

那么对于任意沿zyx转 (γ,π/2,α) 的组合,都等价于 (0,π/2,γ−α) ,而前者有两个自由度( α 和 γ ),后者只有一个自由度( γ 与 α 的差值 γ−α ),这就是万向节锁的问题。
# 四元数
四元数作为一种替代方案,更高效地描述了旋转,并避免了万向节锁问题。虽然 四元数的概念较为复杂,但它在计算机图形学中被广泛应用于物体的旋转。
四元数是一种特殊的复数,通过结合旋转向量和旋转角度,提供了高效的旋转表示方法。其一般形式为q = xi + yj + zk + w,其中x、y、z代表向量的三维坐标,而w代表角度。四元数在描述物体旋转时只需关注这些关键值。
未完待续....
