算法优化——以“LCR 080. 组合”为例
算法优化
算法优化,大体上几个思路:
1. 降低复杂度,比如从循环查找调整为二分查找或者用哈希表来查找,从需要排序到使用优先队列自动排序;
2. 减少重复运算。类似从暴力求解到动态规划;
3. 减少无效运算。如果某个前置条件决定后续所有结果都无效,那么达到前置条件位置时就跳出,避免后续的运算来耗时间耗内存。
下面,将以“LCR 080. 组合”为例来展示下算法优化过程,以及优化的结果。
问题描述
该问题具体描述如下:给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。以下是示例:
显然,这是经典的回溯问题。下面,将从回溯法开始进行求解,并进行算法优化。
算法实现及优化
该问题是经典的回溯问题,那首先用回溯法进行求解
状态一(回溯法)
回溯法的基本原理,就是对当前位置进行循环,然后将当前位置对应的结果进行汇总,具体的不再展开,直接上代码:
class Solution {
public:vector<vector<int>> combine(vector<int> usableNums, int k) {if (k > usableNums.size())return {};vector<vector<int>> results;if (k == 1) {for (auto& num : usableNums) {results.push_back({num});}return results;}for (int i = 0; i < usableNums.size(); ++i) {vector<int> nextNums;for (int j = 0; j < usableNums.size(); ++j) {if (j != i && usableNums[i] < usableNums[j])nextNums.push_back(usableNums[j]);}vector<vector<int>> nextResults = combine(nextNums, k - 1);for (auto& tempResult : nextResults) {vector<int> currentResult = {usableNums[i]};currentResult.insert(currentResult.end(), tempResult.begin(),tempResult.end());results.push_back(currentResult);}}return results;}vector<vector<int>> combine(int n, int k) {vector<int> usableNums(n, 0);for (int i = 0; i < n; ++i) {usableNums[i] = i + 1;}return combine(usableNums, k);}
};
算法性能如下所示:

即对于给定的27个算例,通过时间为98ms,占用内存为42.07MB;
状态二
状态一中,长的组合是短的组合汇总而成,而短的组合又是由更短的组合汇总而来,因此不少相同的短组合会重新计算。比如,[1,3,4,5]和[2,3,4,5]都涉及到[3,4,5]这个短组合,就会算两次。
如果先从最短组合开始算起,就能避免这部分重复运算。因此,状态二先从短组合开始生成,接长为长组合。代码如下:
class Solution {
public:vector<vector<int>> combine(int n, int k) {if (k == 0)return {};vector<vector<int>> results;for (int i = 0; i < n; ++i) {results.push_back({i + 1});}for (int i = 2; i <= k; ++i) {vector<vector<int>> currentResults;for (int j = 0; j < results.size(); ++j) {for (int m = results[j].back() + 1; m <= n; ++m) {vector<int> currentList = results[j];currentList.push_back(m);currentResults.push_back(currentList);}}results = currentResults;}return results;}
};
算法性能如下所示:
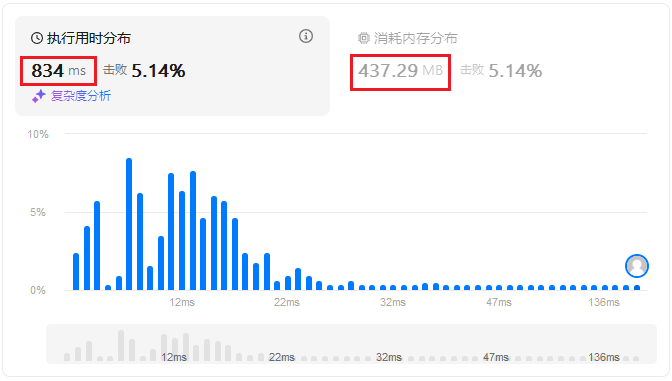
即对于给定的27个算例,通过时间为834ms,占用内存为437.29MB;和状态一相比,时间和内存占用反而是前者的十倍,性能反而差了很多。
为什么会出现相反的效果呢?从代码来看,重复计算肯定已经避免了,能节省一部分时间和空间,但是无效计算增多了。比如,上面代码中循环变语句:for (int m = results[j].back() + 1; m <= n; ++m),循环后的结果,当前循环能产生有效的结果,但下一步或者后面几步,最后几个结果会被过滤掉,存在无效计算。
状态三
针对状态二中存在无效计算的问题,最关键的就是设置合理的循环边界。好的循环边界,既能覆盖所有有效结果,又能将无效计算降到最低。因此,根据每一步的计算实时调整边界。调整后代码如下:
class Solution {
public:vector<vector<int>> combine(int n, int k) {if (k == 0)return {};vector<vector<int>> results;for (int i = 0; i < n; ++i) {results.push_back({i + 1});}int restSize = k - 2;for (int i = 2; i <= k; ++i) {vector<vector<int>> currentResults;for (int j = 0; j < results.size(); ++j) {int endLoc = n - restSize;for (int m = results[j].back() + 1; m <= endLoc; ++m) {vector<int> currentList = results[j];currentList.push_back(m);currentResults.push_back(currentList);}}results = currentResults;restSize = k - i-1;}return results;}
};
算法性能如下图所示:

即对于给定的27个算例,通过时间为25ms,占用内存为24.05MB;和状态一和状态二相比,时间和内存占用都少了很多,算法性能明显提升。
状态四
那针对状态三,算法性能还有没有可能提升呢?经过检查发现,第一次循环还存在无效运算。调整循环的边界,还能减少运行时间。调整后代码如下:
class Solution {
public:vector<vector<int>> combine(int n, int k) {if (k == 0)return {};vector<vector<int>> results;int endLoc = n - (k - 1);for (int i = 0; i < endLoc; ++i) {results.push_back({i + 1});}for (int i = 2; i <= k; ++i) {vector<vector<int>> currentResults;endLoc = n - (k - i );for (int j = 0; j < results.size(); ++j) {for (int m = results[j].back() + 1; m <= endLoc; ++m) {vector<int> currentList = results[j];currentList.push_back(m);currentResults.push_back(currentList);}}results = currentResults;}return results;}
};
算法性能如下图所示:

即对于给定的27个算例,通过时间为15ms,占用内存为23.93MB;和优化前(状态一)相比,占用时间减少了85%,占用内存减少了44%,性能提升明显。
总结
针对已实现的过程,找出其中重复运算的部分以及无效运算的部分,能算法让算法性能明显提升。当然,如果需要更进一步的提升,可能需要更好的思路,或者更好的数据结构。
