贪心、分治和回溯算法

1. 贪心算法

1.1. 贪心算法的概念

• 定义：在求解过程中，始终做出当前状态下看起来“最优”的选择，不回退。
• 核心思想：每一步都选择当前最优解，期望最后得到全局最优解。

适用问题的特征：

• 问题可以分解成多个子问题。
• 每个子问题的局部最优解能构成全局最优解（即贪心选择性质）。
• 子问题之间是相互独立的。

1.2. 贪心算法的使用步骤

1. 识别问题模型：

• 数据有一个 限制值（如背包容量）；
• 有一个 期望值（如总价值、最大数量等）；
• 目标是 在限制值范围内最大化期望值。

2. 设计贪心策略：

• 每一步选取对期望值“最有贡献”的元素；
• 遵循“当前最优选择”原则。

3. 验证贪心策略有效性：

• 举例验证策略是否能得到全局最优解；
• 严格证明较复杂，但通常可通过实际情况判断可行性。

贪心算法的局限性：

• 并非所有问题都适合贪心。
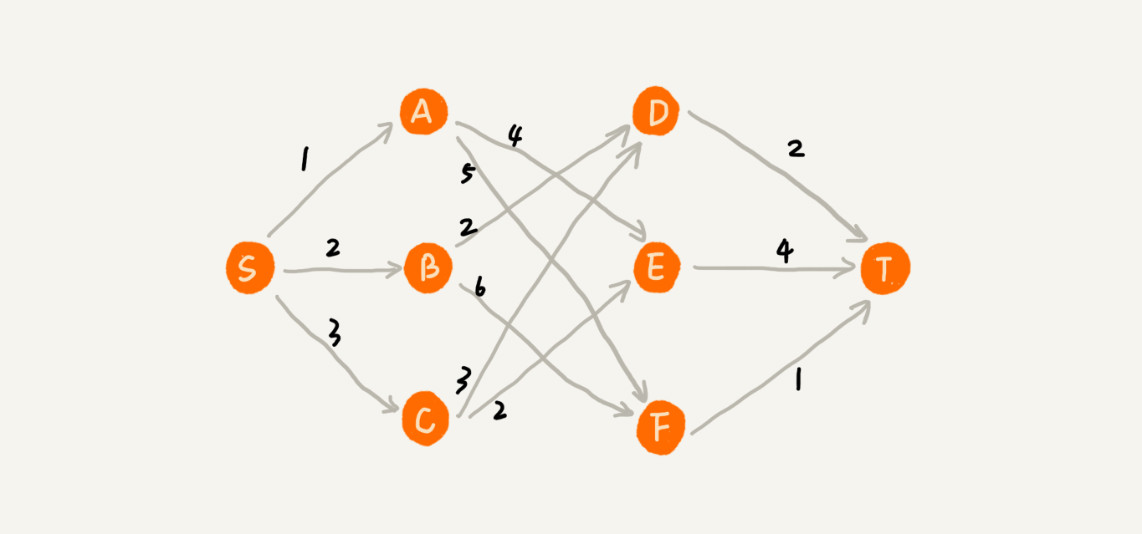
• 示例：图最短路径问题

• • 从 S 到 T 的路径，如果每次都选当前最短边，可能会错过更优的全局路径（如 Dijkstra 可用，BFS/DFS 或 DP更适合）。

• 原因：贪心不回退，前面的错误选择无法弥补。

1.3. Huffman 编码与贪心算法

Huffman 编码简介：

• 一种基于字符频率的压缩编码方式；
• 高频字符使用更短的二进制编码，低频字符使用更长编码；
• 实现数据压缩，广泛用于文件压缩、传输等。

如何利用贪心算法实现？

1. 统计所有字符的出现频率。
2. 将每个字符看作一棵只有一个节点的树，将它们放入最小堆（优先队列）。
3. 重复操作直到只剩下一棵树：

• 每次从堆中取出两棵最小频率的树；
• 合并成一棵新树，新树频率 = 左右子树频率之和；
• 新树再放回堆中。

1. 最终得到的树即为霍夫曼树，由根到叶子的路径即为每个字符的编码。
2. 编码过程中没有一个字符的编码是另一个的前缀。

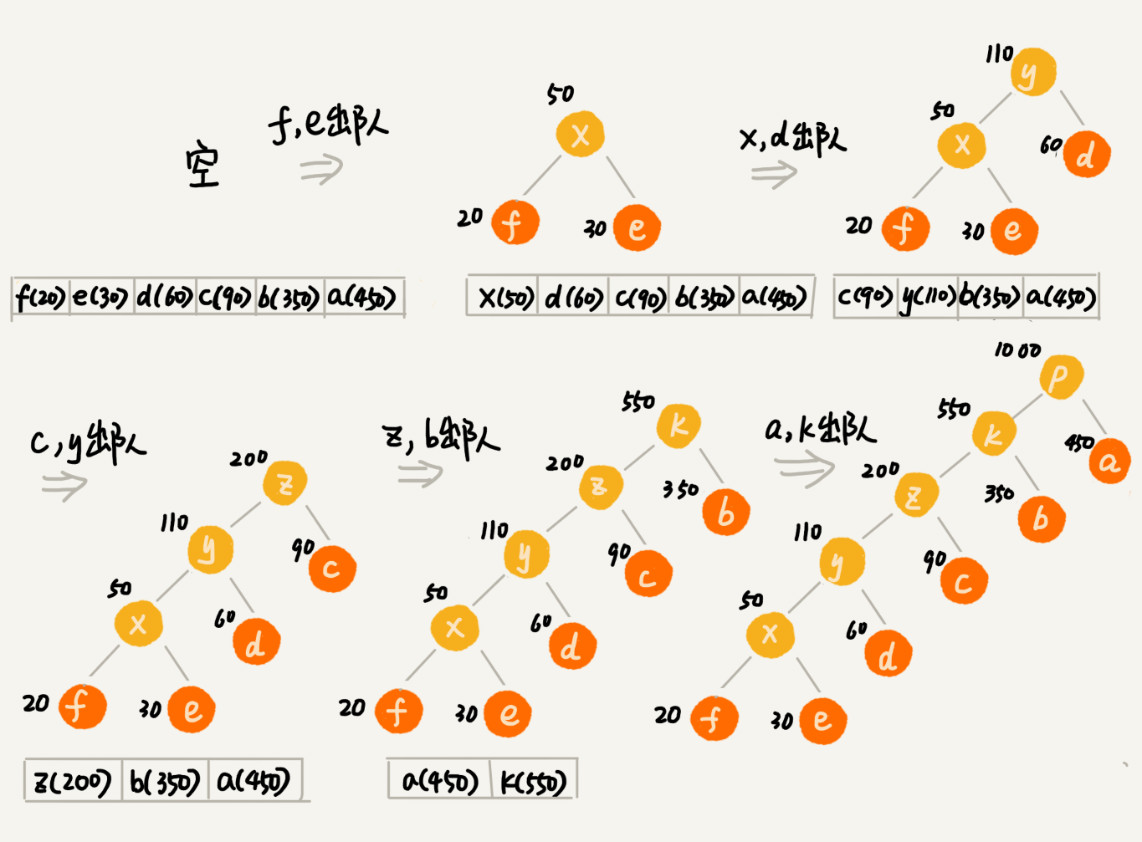
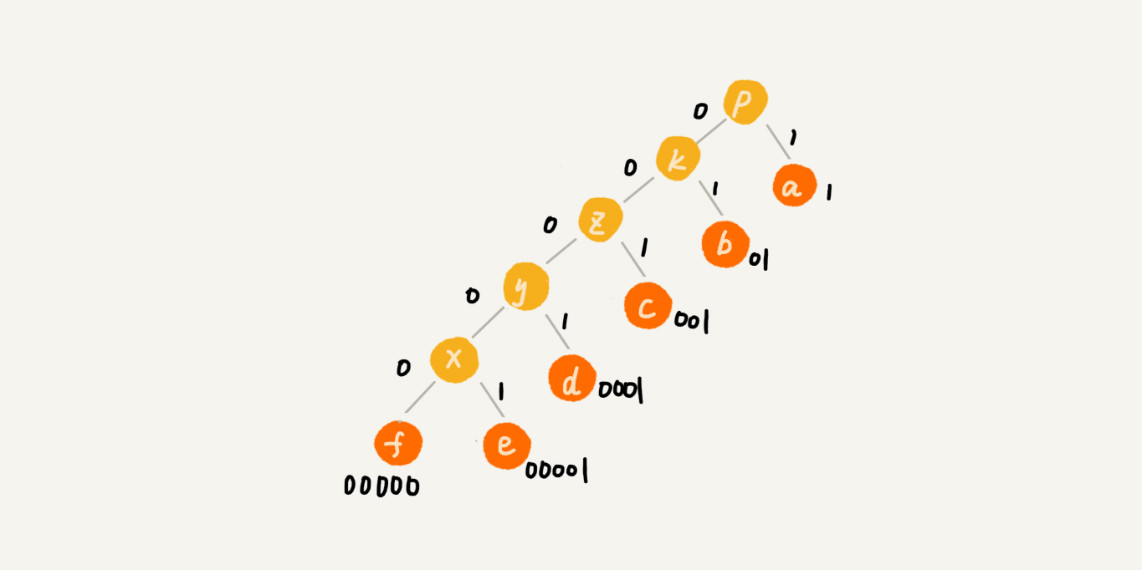
为什么这是贪心？

• 每次都选择频率最小的两个节点进行合并；
• 局部选择最小，最终构成的树有最短的平均编码长度；
• 可证明是最优编码方式之一。

2. 分治算法

2.1. 分治算法的概念

分治算法的定义

分治算法（Divide and Conquer）核心思想：

• 分而治之：将原问题划分成若干规模较小、结构相似的子问题
• 递归解决子问题
• 合并子问题的结果得到原问题的解

实现步骤

1. 分解：将问题分解为子问题
2. 解决：递归求解子问题（足够小可直接解决）
3. 合并：合并子问题的解，得到整体结果

应用条件

• 原问题和子问题结构相似
• 子问题可以独立求解（无依赖）
• 存在终止条件（问题足够小可直接解）
• 合并过程的复杂度不能过高

分治算法要点

• 四字口诀：“分而治之”
• 减少时间复杂度，提高处理效率
• 与递归的关系：分治是思想，递归是实现手段

分治算法两大典型应用

1. 优化算法复杂度（如归并排序 + 逆序对问题）
2. 处理大规模数据（如 MapReduce 并行处理）

2.2. 分治思想的应用

1. 求数组中的逆序对个数

问题定义

• 给定一个数组，统计其中的逆序对个数
• 逆序对：满足 i < j 且 a[i] > a[j] 的元素对
• 暴力解法时间复杂度为 O(n²)

分治优化方案

1. 将数组拆分成两半：A1 和 A2
2. 分别递归求 A1 和 A2 中的逆序对个数：K1、K2
3. 合并时计算 A1 与 A2 之间的逆序对个数：K3
4. 最终结果为：K = K1 + K2 + K3

借助归并排序计算逆序对

• 在归并的过程中，每当发现 a[i] > a[j]，就可确定从 a[i] 到 a[q] 共 (q - i + 1) 个数都与 a[j] 构成逆序对

2. 在大规模数据处理中的应用

实际场景：排序 10GB 文件

• 内存仅 2~3GB，无法一次性加载所有数据
• 分治方案：

• • 按金额区间将数据拆分为若干小文件
  • 各文件内使用内存排序
  • 最后合并排序结果

优势

• 解决大数据内存无法加载问题
• 支持并行处理，加快速度
• 可部署在分布式系统中，如 GFS + 多台机器并行处理

3. MapReduce 的本质是分治思想

MapReduce 简介

• Google 三驾马车之一（另两个：GFS、Bigtable）
• 广泛应用于：倒排索引、PageRank、网页分析等大数据任务

MapReduce 的分治体现

• Map 阶段：将任务拆分，分配给多个节点并行处理（分解+独立求解）
• Reduce 阶段：汇总结果（合并）

核心思想总结

“将大任务拆成小任务并行处理，再合并结果”，本质就是 分治思想

应用案例

• 单词频率统计
• 网页分词、分析（各网页间无依赖）
• 上百亿网页通过 MapReduce 并行处理提高效率

3. 回溯算法

3.1. 回溯算法的概念

回溯 = 暴力搜索 + 剪枝优化 + 递归实现

用剪枝，并不需要穷举搜索所有的情况，从而提高搜索效率。

回溯算法的定义：

回溯是一种“枚举所有可能解路径，并剪枝无效路径”的搜索方法，本质是递归 + 状态恢复。

核心思想：

尝试 - 判断 - 回退 - 再尝试。

可以理解为：在解题过程中不断做选择、走下去，一旦发现不满足要求，就回退到上一步换个方向再尝试。

现实类比理解：电影《蝴蝶效应》

主人公可以回到过去，在关键节点重新做选择，希望达成“最优”的人生结局。

回溯就是在“每个岔路口”尝试所有可能的选择，最终找到最优或满足条件的解。

3.2. 回溯思想的应用

算法问题：

• 八皇后问题
• 数独
• 0-1 背包问题
• 全排列 / 子集生成
• 图着色 / 旅行商问题（TSP）

工程实践：

• 正则表达式匹配
• 编译器语法解析
• 深度优先搜索（DFS 的思想基础）

回溯算法通用解题模型

每一步都做一个决策，尝试所有可能，当不符合预期时“回退”。

步骤：

1. 选择路径：从一组候选项中做出一个选择。
2. 判断合法性：当前路径是否满足约束条件。
3. 递归探索：继续向下探索。
4. 撤销选择（回溯）：如果当前路径走不通，则撤销上一步选择，尝试其他选项。

1. 0-1背包问题

0-1 背包问题：

有 n 个物品，每个物品有一个重量 w[i] 和价值 v[i]，现在有一个容量为 W 的背包，你只能选择放或不放每个物品（不能切割），求在不超过背包容量的情况下，最大可获得的总价值。

回溯思想的核心：

回溯算法是一种逐步探索所有可能选择的算法策略。

对于 0-1 背包来说，每个物品只有两种选择：

放进背包；

不放进背包。

于是就构成了一棵 二叉决策树。我们通过深度优先的方式，遍历整棵决策树，寻找满足条件的最优解。

maxV = 0def knapsack(i, cw, cv):global maxVif cw > W:return  # 剪枝if i == n:maxV = max(maxV, cv)return# 不选第 i 个knapsack(i + 1, cw, cv)# 选第 i 个（如果重量允许）if cw + w[i] <= W:knapsack(i + 1, cw + w[i], cv + v[i])

2. 正则匹配

设定简化版本：

* 表示匹配任意个字符（包括 0 个）

? 表示匹配 0 或 1 个字符

核心思路：

遇到普通字符：匹配即可。

遇到 *：尝试匹配 0 个、1 个、...字符，递归尝试所有情况。

遇到 ?：尝试匹配 0 个或 1 个字符。

匹配失败则回溯到上一个 * 或 ? 重新尝试。

class PatternMatcher:def __init__(self, pattern):self.pattern = patternself.plen = len(pattern)self.matched = Falsedef match(self, text):self.text = textself.tlen = len(text)self.matched = Falseself.rmatch(0, 0)return self.matcheddef rmatch(self, ti, pj):if self.matched:return  # 剪枝：已有匹配结果if pj == self.plen:self.matched = (ti == self.tlen)returnp = self.pattern[pj]if p == '*':for k in range(self.tlen - ti + 1):  # k=0到剩余所有字符self.rmatch(ti + k, pj + 1)elif p == '?':self.rmatch(ti, pj + 1)  # 匹配0个字符if ti < self.tlen:self.rmatch(ti + 1, pj + 1)  # 匹配1个字符elif ti < self.tlen and p == self.text[ti]:self.rmatch(ti + 1, pj + 1)