使用Mathematica绘制Clifford奇异吸引子

Clifford Attractors 是一种由微分方程

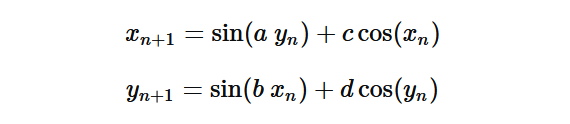
生成的混沌吸引子，参数a,b,c,d不同会产生不同的分形图案。这类吸引子属于迭代函数系统，通过不断迭代参数方程来生成复杂的图形。其数学基础可能与 Clifford 代数或高维函数理论相关，例如 Clifford 代数在四维时空中的应用或 Clifford 分析中的 Dirac 算子与单演函数理论。Clifford Attractors 可能通过非线性微分方程或迭代映射生成，并在分形图像生成、混沌系统模拟或高维数据分析中发挥作用。目前关于 Clifford Attractors 的具体信息较少，需要进一步研究。

使用ListPlot可以简单看到大致图像：

a = -1.24458; b = -1.25191; c = -1.815908; d = -1.90866;
tbl = RecurrenceTable[{x[n + 1] == Sin[a*y[n]] + c*Cos[a*x[n]], y[n + 1] == Sin[b*x[n]] + d*Cos[a*y[n]], x[0] == 0, y[0] == 0}, {x, y}, {n, 1, 25000}];
ListPlot[tbl, PlotRange -> All, Axes -> False, PlotStyle -> Black]

这个图像看起来比较粗糙，可以用ImageAdjust获得更加细致的图形:

a = -1.24458; b = -1.25191; c = -1.815908; d = -1.90866;
cf = Compile[{{pt, _Real, 1}}, {Sin[a pt[[2]]] + c Cos[pt[[1]]], Sin[b pt[[1]]] + d Cos[pt[[2]]]}, CompilationOptions -> {"InlineExternalDefinitions" -> True}];
im = ImageAdjust@Image@BinCounts[Rescale@NestList[cf, {0., 0.}, 1000000], 1/500., 1/500.];
ColorNegate[im^0.5]