匈牙利算法

提示：以下是本篇文章正文内容，下面案例可供参考

一、概念及应用

• 匈牙利算法（Hungarian Algorithm）是一种用于解决​​任务分配问题​​（Assignment Problem）的组合优化算法，能够在多项式时间内找到最优解。其核心目标是在给定的成本或收益矩阵中，找到一组​​不同行不同列的零元素​​，从而实现最小化总成本或最大化总收益的分配方案

• 问题场景​​：将n个任务分配给n个工人，每人仅负责一项任务，每项任务仅由一人完成，且分配成本已知（如工时、运费等）。
  ​​目标​​：找到总成本最低的分配方案。

二、实现过程（简化版）

对于n匹配n,即nn的矩阵：
​​矩阵预处理​​：
​​行减法​​：每行减去该行最小值，使每行至少有一个0。
​​列减法​​：每列减去该列最小值，使每列至少有一个0。
​​覆盖零元素​​：
用最少的横线或竖线覆盖所有0。若最少线条数=n，则已找到最优解；否则进入调整步骤。
​​调整矩阵​​：
找到未被覆盖的最小值，未覆盖元素减去该值，交点元素加上该值，生成新的0。
​​匹配零元素​​：
选择位于不同行、不同列的0作为匹配，最终得到最优分配方案；
即先找行里只有一个0的行，这个0必选，它对于的横纵元素就是最有匹配，这是去掉该行该列，在（n-1）（n-1）里继续上述过程，直到结束

总结

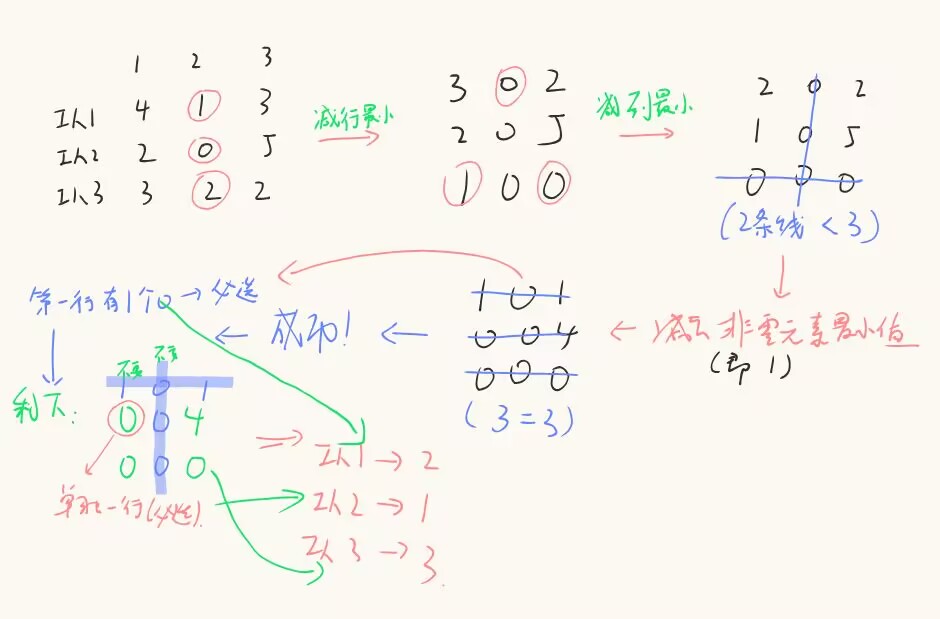
假设3个工人和3个任务的成本矩阵如下：

声明：
本文为本人的学习笔记，旨在记录和分享个人在学习过程中的心得体会和原创代码。由于本人刚入门，对相关知识的理解可能还存在不足之处，文章中难免会有错误或不准确的地方。在此，我诚挚地欢迎各位读者在阅读过程中，如果发现任何问题或有其他建议，随时在评论区或通过其他方式与我交流。我将虚心听取大家的意见，及时修正和改进文章内容，以便更好地学习和成长。感谢大家的关注和支持！