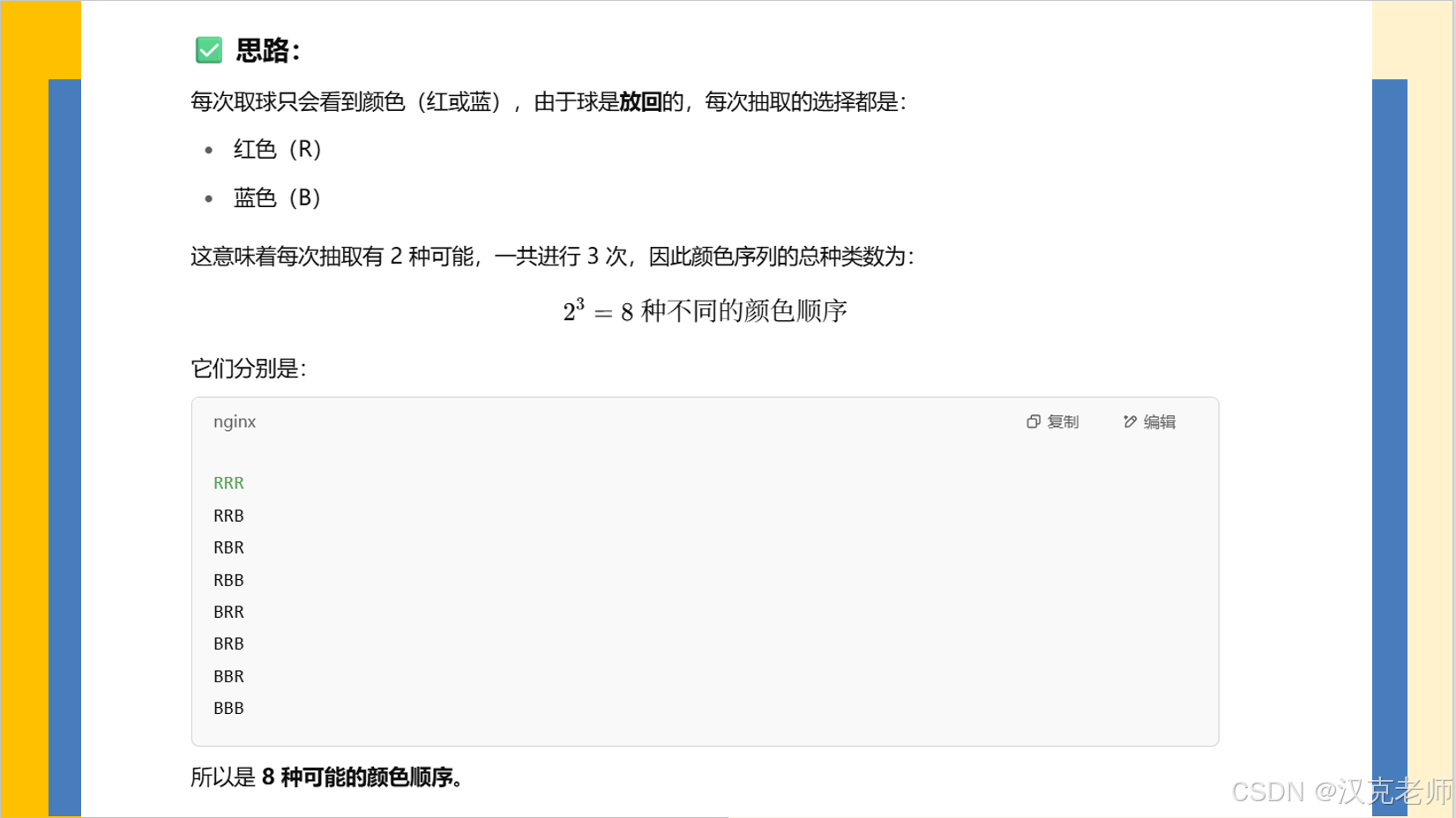
GESP2024年3月认证C++八级( 第二部分判断题(1-5))





















 孙子定理参考程序:
孙子定理参考程序:
#include <iostream>
#include <vector>
using namespace std;// 扩展欧几里得算法:用于求逆元
int extendedGCD(int a, int b, int &x, int &y) {if (b == 0) {x = 1; y = 0;return a;}int x1, y1;int gcd = extendedGCD(b, a % b, x1, y1);x = y1;y = x1 - (a / b) * y1;return gcd;
}// 求模逆元:ax ≡ 1 (mod m)
int modInverse(int a, int m) {int x, y;int g = extendedGCD(a, m, x, y);if (g != 1) {throw runtime_error("不存在逆元,模数必须互质");}return (x % m + m) % m; // 保证正数
}// 中国剩余定理实现
int chineseRemainder(const vector<int>& a, const vector<int>& m) {int M = 1;int n = a.size();for (int i = 0; i < n; ++i) {M *= m[i];}int result = 0;for (int i = 0; i < n; ++i) {int Mi = M / m[i];int inv = modInverse(Mi, m[i]);result += a[i] * Mi * inv;}return result % M;
}int main() {// 示例输入vector<int> a = {2, 3, 2}; // 余数vector<int> m = {3, 5, 7}; // 模数(需互质)try {int x = chineseRemainder(a, m);cout << "x ≡ " << x << " mod " << (3 * 5 * 7) << endl;} catch (exception &e) {cout << "错误: " << e.what() << endl;}return 0;
}