高等数学第三章---微分中值定理与导数的应用（§3.6 函数图像的描绘§3.7 曲率）

§3.6 函数图像的描绘

一、曲线的渐近线

对于某些函数，其图形向无穷远处延伸时，会越来越趋近于某一条直线，这条直线被称为曲线的渐近线 (Asymptote)。

1. 定义

若曲线 $y=f(x)$ 上一点 $P(x,y)$ 沿曲线趋于无穷远时，该点 $P$ 与某一直线 $L$ 的距离趋于 0，则称直线 $L$ 为曲线 $y=f(x)$ 的渐近线。

2. 渐近线的求法

(1) 斜渐近线 (Oblique Asymptote)

假设直线 $L:y=kx+b$ 是曲线 $y=f(x)$ 的渐近线。我们需要确定常数 $k$ 和 $b$。
根据点到直线的距离公式，点 $P(x,f(x))$ 到直线 $L$ 的距离为：
$$d=\frac{|f(x)-(kx+b)|}{\sqrt{1+k^2}}$$
由渐近线的定义可知，当点 $P$ 沿曲线趋于无穷远（即 $x\to \infty$ 或 $x\to -\infty$）时，距离 $d\to 0$。由于 $\sqrt{1+k^2}$ 是一个非零常数，这等价于：
$$\underset{x\to \pm \infty }{\lim }[f(x)-(kx+b)]=0$$
由此可以推导出 $k$ 和 $b$ 的计算公式：

1. 求 $k$:
   上式两边同除以 $x$（假设 $x\ne 0$）：
   $$\underset{x\to \pm \infty }{\lim }\left[\frac{f(x)}{x}-k-\frac{b}{x}\right]=0$$
   由于当 $x\to \pm \infty$ 时，$\frac{b}{x}\to 0$，因此得到：
   $$\boxed{k=\underset{x\to \pm \infty }{\lim }\frac{f(x)}{x}}$$
   如果这个极限存在且有限，则计算下一步。

2. 求 $b$:
   由 ${\lim }_{x\to \pm \infty }[f(x)-kx-b]=0$ 可得：
   $$\boxed{b=\underset{x\to \pm \infty }{\lim }[f(x)-kx]}$$
   将第一步求得的 $k$ 代入此式，如果这个极限存在且有限，则直线 $y=kx+b$ 就是曲线的斜渐近线（或水平渐近线）。

注意: $x\to +\infty$ 和 $x\to -\infty$ 的极限可能不同，需要分别计算，可能得到不同的渐近线。

(2) 水平渐近线 (Horizontal Asymptote)

当斜渐近线的斜率 $k=0$ 时，其方程为 $y=b$。此时，计算 $b$ 的公式变为：
$$b=\underset{x\to \pm \infty }{\lim }[f(x)-0\cdot x]=\underset{x\to \pm \infty }{\lim }f(x)$$
因此，若极限 ${\lim }_{x\to \pm \infty }f(x)=b$ 存在且有限，则直线 $y=b$ 是曲线的水平渐近线。这是斜渐近线的特例。

(3) 垂直渐近线 (Vertical Asymptote)

如果在某点 $x=x_0$ 附近，函数值趋于无穷大，即：
$$\underset{x\to x_0}{\lim }f(x)=\infty (\text{或}-\infty )$$
或者单侧极限
$$\underset{x\to x_0^{+}}{\lim }f(x)=\infty (\text{或}-\infty )\text{或}\underset{x\to x_0^{-}}{\lim }f(x)=\infty (\text{或}-\infty )$$
成立，则直线 $x=x_0$ 是曲线的垂直渐近线。
通常在函数定义域的边界点或使分母为零的点寻找垂直渐近线。

示例

例 1： 求 $y=\frac{x^3}{x^2+1}$ 的渐近线。
(解：待补充)

例 2： 求 $y=\frac{x^2+x}{x^2-1}$ 的渐近线。
(解：待补充)

例 3： 求 $y=\frac{1}{x}+\ln (1+e^x)$ 的渐近线。
(解：待补充)

---

二、函数图形的作法

描绘函数 $y=f(x)$ 图形的大致步骤如下：

1. 确定定义域: 求出使函数表达式有意义的自变量 $x$ 的取值范围。
2. 考察对称性与周期性:
   • 奇偶性: 判断 $f(-x)$ 与 $f(x)$ 的关系。若 $f(-x)=f(x)$，则为偶函数，图形关于 $y$ 轴对称；若 $f(-x)=-f(x)$，则为奇函数，图形关于原点对称。
   • 周期性: 判断是否存在常数 $T>0$ 使得 $f(x+T)=f(x)$ 对定义域内所有 $x$ 成立。若存在，则只需分析一个周期长度的区间。
3. 研究单调性与极值:
   • 计算一阶导数 $f^{\prime }(x)$。
   • 求出 $f^{\prime }(x)=0$ 的点（驻点）和 $f^{\prime }(x)$ 不存在的点（可能是极值点）。
   • 用这些点划分定义域，列表分析 $f^{\prime }(x)$ 的符号，确定函数的单调递增和递减区间。
   • 根据一阶导数在驻点或不可导点两侧的符号变化，判断并计算极大值和极小值。
4. 研究凹凸性与拐点:
   • 计算二阶导数 $f^{\prime \prime }(x)$。
   • 求出 $f^{\prime \prime }(x)=0$ 的点和 $f^{\prime \prime }(x)$ 不存在的点。
   • 用这些点划分定义域，列表分析 $f^{\prime \prime }(x)$ 的符号，确定曲线的凹区间（$f^{\prime \prime }>0$，Concave Up）和凸区间（$f^{\prime \prime }<0$，Concave Down）。
   • 判断凹凸性发生变化的连续点，计算拐点坐标。
5. 确定渐近线: 按照前面介绍的方法，求出函数的水平渐近线、垂直渐近线和斜渐近线。
6. 确定特殊点的坐标: 计算一些关键点的坐标，例如：
   • 与坐标轴的交点（令 $x=0$ 求 $y$ 截距，令 $y=0$ 求 $x$ 截距）。
   • 极值点、拐点。
7. 描绘图形: 综合以上信息（定义域、对称性、周期性、单调区间、极值、凹凸区间、拐点、渐近线、特殊点），描绘出函数图形的草图。

示例

例 4： 作 $y=\frac{4(x+1)}{x^2}-2$ 的图形。
(解：待补充)

---

§3.7 曲率

一、曲率的概念

1. 曲率 (Curvature): 描述曲线弯曲程度的量。直观地说，曲线越弯曲，曲率越大；直线或接近直线的部分，曲率越小（直线曲率为0）。

2. 与曲率有关的量:
   考察曲线上某点附近的弯曲程度，可以考虑一小段弧。

   • (1) 切线转动角度的大小: 在相同弧长上，切线方向变化的角度越大，曲线弯曲程度越大。如下图示意，弧 $M_1{M}_2$ 较平缓，切线转角 $\Delta {\alpha }_1$ 较小；弧 $M_2{M}_3$ 较弯曲，切线转角 $\Delta {\alpha }_2$ 较大。
     

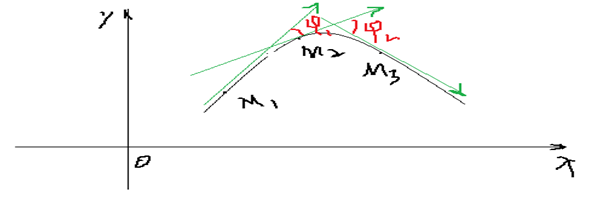
   • (2) 曲线的弧长大小: 曲线的弧长越小，曲线的弯曲程度越大。如图，弧$M_1{M}_2$与弧$N_1{N}_2$切线转角相同，但弯曲程度不一样，显然，弧长小的弯曲程度大。
     

   结论: 曲线的弯曲程度与切线转动角度成正比，与曲线弧长成反比。

二、曲率计算

1. 弧微分 (Arc Differential)

设曲线 $y=f(x)$ 在 $(a,b)$ 内具有连续导数 $f^{\prime }(x)$ (保证曲线光滑且弧长可积)。
考虑曲线上点 $(x,y)$ 到邻近点 $(x+\Delta x,y+\Delta y)$ 的一小段弧长 $\Delta s$。当 $\Delta x$ 很小时，弧长 $\Delta s$ 可以用弦长 $\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}$ 来近似。
$$\Delta s\approx \sqrt{(\Delta x{)}^2+(\Delta y{)}^2}=\sqrt{1+{\left(\frac{\Delta y}{\Delta x}\right)}^2}|\Delta x|$$
当 $\Delta x\to 0$ 时，$\frac{\Delta y}{\Delta x}\to y^{\prime }$。取其微分形式，得到弧微分 $ds$:
$$\boxed{ds=\sqrt{1+(y^{\prime }{)}^2}dx}(\text{假设 }dx>0)$$
或写成对称形式：$d{s}^2=d{x}^2+d{y}^2$。弧微分 $ds$ 代表了弧长 $s$ 的微小改变量。

2. 曲率计算公式

设曲线上一点 $M$ 处的切线与 $x$ 轴正向的夹角为 $\alpha$。当点从 $M$ 移动到邻近点 $M^{\prime }$ 时，弧长变化了 $\Delta s$，切线转角变化了 $\Delta \alpha$。
定义弧 $M{M}^{\prime }$ 上的平均曲率 $\bar{k}$ 为：
$$\bar{k}=\left|\frac{\Delta \alpha }{\Delta s}\right|$$
表示单位弧长上切线转角的平均变化率。
当点 $M^{\prime }\to M$（即 $\Delta s\to 0$）时，平均曲率的极限即为点 $M$ 处的曲率 $k$：
$$\boxed{k=\underset{\Delta s\to 0}{\lim }\left|\frac{\Delta \alpha }{\Delta s}\right|=\left|\frac{d\alpha }{ds}\right|}$$

现在推导用 $y^{\prime },y^{\prime \prime }$ 表示的曲率公式：
已知切线的斜率 $\tan \alpha =y^{\prime }$。两边对 $x$ 求导：
$$\frac{d}{dx}(\tan \alpha )=\frac{d}{dx}(y^{\prime })$$
$${\sec }^2\alpha \frac{d\alpha }{dx}=y^{\prime \prime }$$
$$(1+{\tan }^2\alpha )\frac{d\alpha }{dx}=y^{\prime \prime }$$
$$(1+(y^{\prime }{)}^2)\frac{d\alpha }{dx}=y^{\prime \prime }$$
所以$\frac{d\alpha }{dx}=\frac{y^{\prime \prime }}{1+(y^{\prime }{)}^2}$。
根据链式法则 $\frac{d\alpha }{ds}=\frac{d\alpha /dx}{ds/dx}$，以及 $ds/dx=\sqrt{1+(y^{\prime }{)}^2}$，可得：
$$\frac{d\alpha }{ds}=\frac{\frac{y^{\prime \prime }}{1+(y^{\prime }{)}^2}}{\sqrt{1+(y^{\prime }{)}^2}}=\frac{y^{\prime \prime }}{(1+(y^{\prime }{)}^2{)}^{3/2}}$$
代入曲率定义 $k=\left|\frac{d\alpha }{ds}\right|$，得到直角坐标系下的曲率公式：
$$\boxed{k=\frac{|y^{\prime \prime }|}{(1+(y^{\prime }{)}^2{)}^{3/2}}}$$

注：
若曲线由参数方程给出：
$$\{\begin{array}{l}x=x(t)\\ y=y(t)\end{array}$$
则曲率公式为：
$$\boxed{k=\frac{|x^{\prime }{y}^{\prime \prime }-x^{\prime \prime }{y}^{\prime }|}{(x^{\prime 2}+y^{\prime 2}{)}^{3/2}}}$$
其中 $x^{\prime },y^{\prime }$ 表示对参数 $t$ 的一阶导数，$x^{\prime \prime },y^{\prime \prime }$ 表示对参数 $t$ 的二阶导数。

示例

例 1： 计算双曲线 $xy=1$ 在点 $(1,1)$ 处的曲率。
(解：待补充)

例 2： 抛物线 $y=a{x}^2+bx+c$ ($a\ne 0$) 上哪一点的曲率最大？
(解：待补充)

例 3： 设圆的参数方程为
$$\{\begin{array}{l}x=R\cos t\\ y=R\sin t\end{array}$$
求圆上任意点处的曲率。
(解：待补充)

三、曲率圆与曲率半径

设曲线 $y=f(x)$ 在点 $M$ 处的曲率为 $k$ ($k\ne 0$)。
在点 $M$ 处的法线上，在曲线凹的一侧取点 $D$，使得线段 $DM$ 的长度为 $\rho =\frac{1}{k}$。
以 $D$ 为圆心，$\rho$ 为半径作圆。这个圆称为曲线在点 $M$ 处的曲率圆 (Circle of Curvature)。其半径 $\rho =\frac{1}{k}$ 称为曲线在点 $M$ 处的曲率半径 (Radius of Curvature)。

曲率圆在点 $M$ 处与原曲线具有相同的切线、相同的曲率，并且在点 $M$ 附近与原曲线吻合得最好（二阶接触）。曲率半径 $\rho$ 直观地表示了在该点附近最能近似曲线的圆的半径。曲率越大，曲率半径越小，表示曲线弯曲得越厉害。