2024年US SCI1区TOP：自适应变异麻雀搜索算法AMSSA+地铁隧道变形预测，深度解析+性能实测

---

1.摘要

本文提出了AMSSA-Elman-AdaBoost耦合模型，该模型将Elman-AdaBoost与自适应变异麻雀搜索算法（AMSSA）相结合，用于预测软土地层中邻近深基坑开挖引发的既有地铁隧道变形。AMSSA算法采用混沌序列生成初始种群，增强了个体分布的遍历性和随机性，从而提高了算法的全局搜索能力。AMSSA引入Tent混沌扰动和柯西变异算子，有效避免了种群过早收敛或过度分散的问题，增强了局部搜索能力。自适应平衡策略提出了生产者-跟随者数量的自适应调整公式，实现了全局探索与局部开发能力的动态平衡。

2.麻雀搜索算法SSA原理

【智能算法】麻雀搜索算法（SSA）原理及实现

3.改进策略

Cat映射混沌

采用Cat映射混沌序列对种群进行初始化：
$$\left[\begin{array}{c}{y}_{i+1}\\ w_{i+1}\end{array}\right]=\left[\begin{array}{cc}1& a_1\\ b_1& a_1{b}_1+1\end{array}\right]\left[\begin{array}{c}{y}_i\\ w_i\end{array}\right]\mathrm{mod}1$$

根据cat映射的特点，在可行域上生成混沌序列并用反解初始化混沌序列:
$$\{\begin{array}{c}{\mathbf{Y}}^{\prime }=\left[\begin{array}{c}{Y}_1^{\prime },Y_2^{\prime },\cdots ,Y_d^{\prime },\cdots ,Y_d^{\prime }\end{array}\right]\\ y_{id}=q(b_{id}^1-b_{id}^{\mathrm{u}})-y_{id}\end{array}$$

动态调整机制

采用Tent混沌映射和柯西变异：
$$\mathrm{mutation}(x)=x(1+\tan (\pi (u-0.5)))$$

修正生产者位置更新：
$$x_{i,d}^{t+1}=\{\begin{array}{ll}{x}_{i,d}^t\cdot \frac{2}{\exp {\left(\frac{4i}{\alpha \cdot \mathrm{itermax}}\right)}^m},R_2<\mathrm{ST}& \\ x_{i,d}^t+Q\times L,R_2⩾\mathrm{ST}& \end{array}$$

自适应调整策略

本文提出了生产者-跟随者自适应调整策略：在迭代初期，生产者将占据种群大多数；随着迭代次数增加，生产者数量自适应递减而跟随者数量相应递增，逐步实现从全局搜索到局部精确搜索的切换，从而整体提升收敛精度。

$$\begin{array}{rl}& \begin{array}{r}r=b(\tan (-\frac{\pi t}{4\cdot {\mathrm{iter}}_{\max }}+\frac{\pi }{4})-k\cdot \mathrm{rand}(0,1)),\end{array}\\ & p_{\mathrm{Num}}=r\cdot N,\\ & \begin{array}{r}{s}_{\mathrm{Num}}=(1-r)\cdot N.\end{array}\end{array}$$

流程图

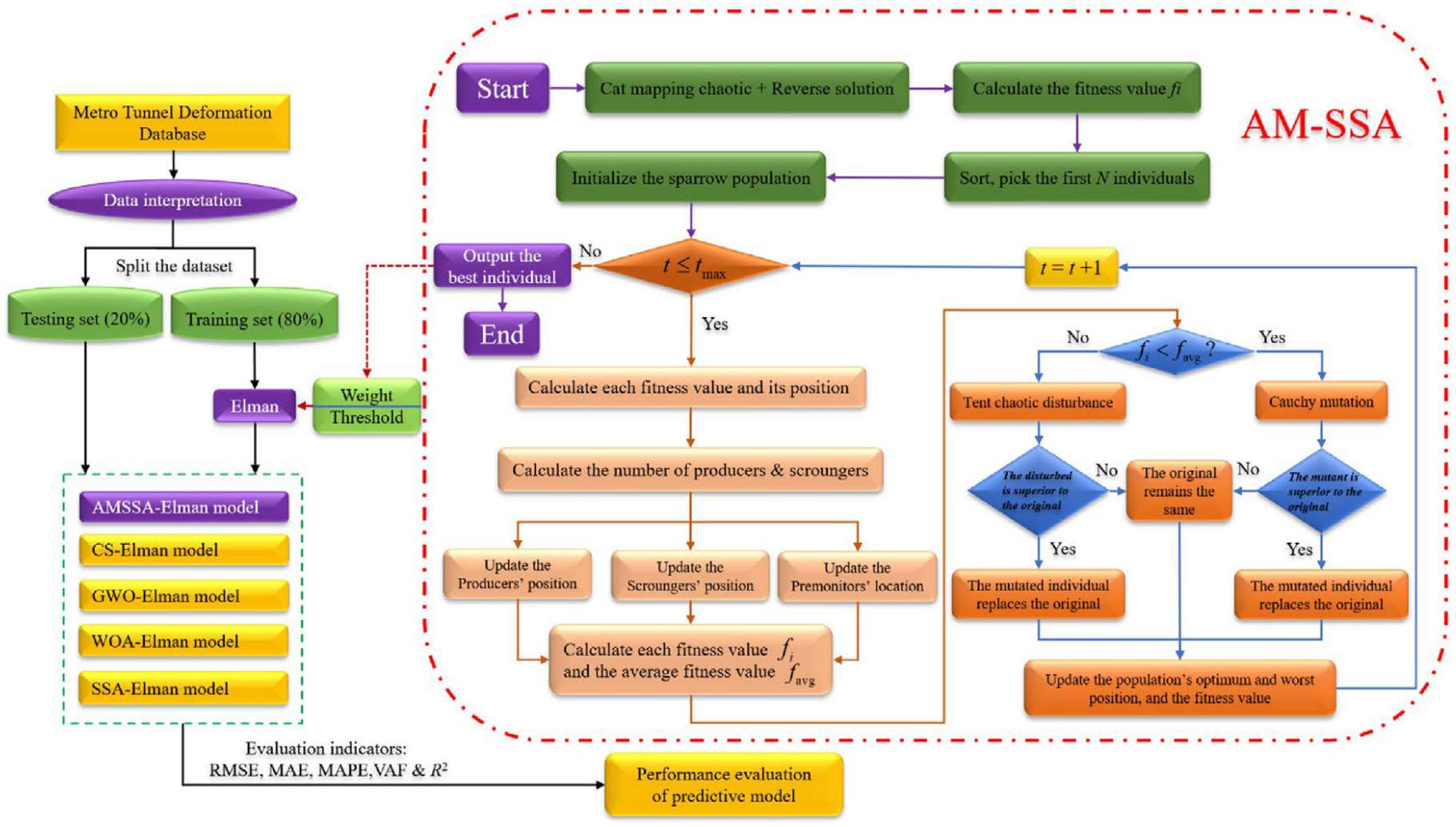
4.结果展示

5.参考文献

[1] Zhou X, Hu W, Zhang Z, et al. Adaptive mutation sparrow search algorithm-Elman-AdaBoost model for predicting the deformation of subway tunnels[J]. Underground Space, 2024, 17: 320-360.

6.代码获取

7.读者交流