ROC 曲线 和 AUC

在目标检测中，一些基本概念是肯定绕不开的，早晚得学。因此，读者在阅读这篇之前，可以看一看另一篇关于Precision和Recall的帖子.

假设你已经看过上一篇了，那么我们开始：

ROC曲线也是用到了2个变量，TPR（True Positive Rate）和FPR（False Positive Rate）。其中，TPR的定义与Recall的定义完全相同。这里为了方便，贴出上一篇帖子中的图片：

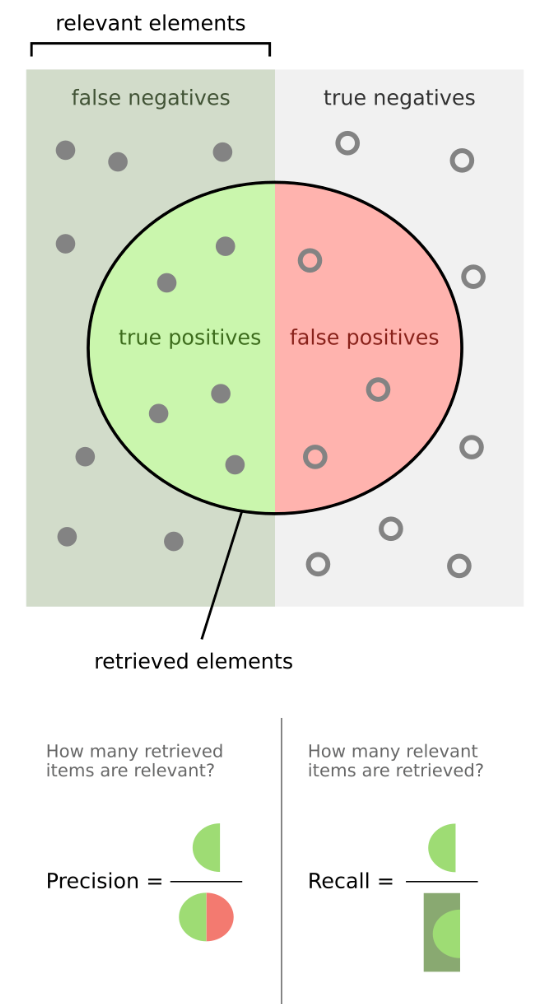
而FPR呢？和TPR相对应，代表右边部分的半圆占右边部分矩形面积的比例。也就是TPR=FP / (FP+TN)。

TPR越大越好，FPR越小越好。

而二元分类时输出的是0~1的概率，那么threshold的选取不同，就会导致不同的分类结果。于是，我们分别选取多个不同的threshold，就会得到多个不同的二元组（TPR，FPR），从而绘制出点图。再将点之间进行连接，就得到了ROC曲线：

在此图中，虚线表示随机乱猜，紫线表示一个完美的分类器，蓝线表示一般分类器的分类结果。注意，ROC曲线一定会经过（0，0）和（1，1）两点，代表全部分类为负和全部分类为正的结果。在此基础上可以看到，其实完美分类器只对应于（0，1）这个点而已。

也就是说，（TPR，FPR）离（0，1）越近越好。那么，我们怎样衡量这种”接近“？答案是，可以采用计算对应曲线与坐标轴围成的面积，AUC（Area Under Curve）。

不难观察到，紫色曲线的AUC，也就是在0到1区间上的积分为1，虚线（乱猜）的AUC为0.5，一般分类器的AUC在0.5到1之间。