机器学习入门实践:加州房价预测从 0 到 1 全过程
![]() 对于机器学习新手来说,最直观的学习方式就是动手跑通一个完整项目。本文将以 “加州房价预测” 为例,带你从代码编写到结果解读,完整体验机器学习的核心流程 —— 从数据准备到模型评估,每个步骤都附详细说明,帮你轻松入门。
对于机器学习新手来说,最直观的学习方式就是动手跑通一个完整项目。本文将以 “加州房价预测” 为例,带你从代码编写到结果解读,完整体验机器学习的核心流程 —— 从数据准备到模型评估,每个步骤都附详细说明,帮你轻松入门。
一、准备工具:导入必要的 Python 库和基础设置
首先,我们需要导入几个常用的 Python 库,它们就像 “工具箱”,分别负责数据处理、模型训练和结果展示:
# ==================== 1. 导入必要工具库 ====================
# 数值计算工具
import numpy as np
# 表格数据处理工具
import pandas as pd
# 加载加州房价数据集
from sklearn.datasets import fetch_california_housing
# 划分训练/验证/测试集
from sklearn.model_selection import train_test_split
# 特征标准化(统一数据尺度)
from sklearn.preprocessing import StandardScaler
# 线性回归模型(核心预测模型)
from sklearn.linear_model import LinearRegression
# 模型评估指标(均方误差、决定系数)
from sklearn.metrics import mean_squared_error, r2_score
# 画图工具(直观展示结果)
import matplotlib.pyplot as plt
# 解决matplotlib中文显示乱码问题
from matplotlib.font_manager import FontManager# ==================== 2. 基础设置(确保结果可复现+中文正常显示) ====================
# 固定随机种子:让每次运行代码的结果一致,便于调试和复现
np.random.seed(42)# 配置中文字体:避免画图时中文标签乱码
fm = FontManager()
# 筛选系统中包含“黑”“宋”“microsoft”的中文字体(覆盖大部分系统)
available_fonts = [f for f in fm.get_font_names() if any(['hei' in f.lower(), 'song' in f.lower(), 'microsoft' in f.lower()]
)]
if available_fonts:plt.rcParams["font.family"] = available_fonts[0]
else:print("未找到可用中文字体,将使用默认英文显示")
库介绍
NumPy (np)
NumPy 是 Python 科学计算领域的核心基础库,也是众多高级数据分析和机器学习库(如 Scikit-learn、Pandas)的底层依赖。其名称来源于 “Numerical Python”,专为高效处理大型多维数组(ndarray)和执行数值计算而设计。它的核心优势在于提供了简洁且高性能的接口,能够快速完成数组的创建、索引、切片、重塑以及各类数学运算(如线性代数、傅里叶变换、随机数生成等)。由于其内部运算基于 C 语言实现,相比 Python 原生列表,NumPy 在处理大规模数据时,能显著减少内存占用并提升计算速度,是后续进行数据清洗、特征工程、模型训练等机器学习流程的 “基石”。
Pandas
虽然 Pandas 主要用于数据处理和分析,但在机器学习中也非常重要,因为它提供了强大的数据结构(如 DataFrame)来处理表格数据。
Scikit-learn (
sklearn)Scikit-learn 是一个基于 Python 的开源机器学习库。它提供了简单有效的数据挖掘和数据分析工具。它构建在 NumPy、SciPy 和 matplotlib 之上,支持多种监督和非监督学习算法。
函数介绍
fetch_california_housing()这是
sklearn.datasets模块中的一个函数,用于加载加州房价数据集。该数据集包含了每个地区的人口统计信息以及房价中位数。返回的数据包含特征矩阵和目标向量,适用于回归问题的研究与实践。train_test_split()此函数来自
sklearn.model_selection,用于将数据集划分为训练集和测试集(或验证集)。这对于评估模型性能非常关键,确保模型能够在未见过的数据上表现良好。参数包括输入数据、测试集大小以及随机种子等。StandardScaler()StandardScaler来自sklearn.preprocessing,用于标准化特征,使其具有零均值和单位方差。这是许多机器学习算法的重要预处理步骤,因为这些算法对输入变量的规模敏感。LinearRegression()LinearRegression是sklearn.linear_model中的一个类,实现了普通最小二乘线性回归。它用于拟合线性模型,通过找到最佳参数使预测值与实际观测值之间的误差平方和最小化。mean_squared_error(),r2_score()这两个函数都属于
sklearn.metrics模块,分别用于计算均方误差(MSE)和决定系数(R²)。它们是评估回归模型性能的常用指标。MSE 衡量了模型预测值与真实值之间差异的平方的平均值,R² 则衡量了模型解释变异性的能力,其值越接近1表示模型越好。
二、第一步:加载数据,先搞懂 “我们要预测什么”
机器学习的第一步是 “认识数据”。我们用加州房价数据集,它包含了加州各区域的房价,以及 8 个可能影响房价的因素(比如收入、房龄、地理位置等)。
代码实现:
# ==================== 3. 加载并探索数据 ====================
# 加载加州房价数据集(sklearn自带,无需手动下载)
housing = fetch_california_housing()
# X:特征数据(影响房价的8个因素),y:目标数据(房价中位数,单位:万美元)
X_full, y_full = housing.data, housing.target# 简化数据:从20640条原始数据中随机抽取100条,降低计算量,适合新手演示
n_samples = 100
# 随机选择100个样本的索引(不重复)
indices = np.random.choice(len(X_full), size=n_samples, replace=False)
X = X_full[indices] # 100个样本的特征(形状:(100, 8))
y = y_full[indices] # 100个样本的房价(形状:(100,))# 打印数据基本信息,快速了解数据结构
print("="*60)
print("【1. 数据集基本信息】")
print("="*60)
print(f"特征矩阵形状:{X.shape} → 100个区域样本,每个样本8个特征")
print(f"房价向量形状:{y.shape} → 100个区域的房价数据")
print(f"8个特征名称:{housing.feature_names}")
print(f"房价范围:{y.min():.1f} 万 ~ {y.max():.1f} 万美元")
print(f"特征说明:\n- MedInc:区域平均收入\n- HouseAge:区域平均房龄\n- AveRooms:区域平均房间数\n- AveBedrms:区域平均卧室数\n- Population:区域人口数\n- AveOccup:区域平均家庭人口\n- Latitude:纬度(地理位置)\n- Longitude:经度(地理位置)")运行结果解读:
============================================================
【1. 数据集基本信息】
============================================================
特征矩阵形状:(100, 8) → 100个区域样本,每个样本8个特征
房价向量形状:(100,) → 100个区域的房价数据
8个特征名称:['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
房价范围:0.5 万 ~ 5.0 万美元
特征说明:
- MedInc:区域平均收入
- HouseAge:区域平均房龄
- AveRooms:区域平均房间数
- AveBedrms:区域平均卧室数
- Population:区域人口数
- AveOccup:区域平均家庭人口
- Latitude:纬度(地理位置)
- Longitude:经度(地理位置)三、第二步:划分数据集,避免 “模型作弊”
如果用同一组数据 “既当练习题,又当考试卷”,模型会 “死记硬背” 答案(这叫 “过拟合”),遇到新数据就会出错。因此,我们需要把数据分成 3 部分:
| 数据集 | 比例 | 作用 | 类比 |
|---|---|---|---|
| 训练集 | 70% | 教模型学习规律 | 平时练习题 |
| 验证集 | 15% | 调整模型参数,优化效果 | 模拟考试 |
| 测试集 | 15% | 最终评估模型的真实预测能力 | 期末考试 |
代码实现:
# ==================== 4. 划分数据集(避免模型"作弊") ====================
# 原则:训练集学规律,验证集调参数,测试集评真实能力(测试集仅用一次!)
# 第一步:先从所有数据中划分"测试集"(占比15%,相当于期末考试卷)
X_temp, X_test, y_temp, y_test = train_test_split(X, y,test_size=0.15, # 测试集占总数据的15%random_state=42 # 固定随机种子,确保划分结果一致
)# 第二步:从剩余85%数据中划分"训练集"(70%)和"验证集"(15%)
X_train, X_val, y_train, y_val = train_test_split(X_temp, y_temp,test_size=0.15/0.85, # 验证集占剩余数据的比例,确保总占比15%random_state=42
)# 打印划分结果
print("\n" + "="*60)
print("【2. 数据集划分结果】")
print("="*60)
print(f"训练集:{X_train.shape[0]} 个样本(70%,用于模型学习规律)")
print(f"验证集:{X_val.shape[0]} 个样本(15%,用于调整模型参数)")
print(f"测试集:{X_test.shape[0]} 个样本(15%,用于评估真实预测能力)")运行结果解读:
============================================================
【2. 数据集划分结果】
============================================================
训练集:69 个样本(70%,用于模型学习规律)
验证集:16 个样本(15%,用于调整模型参数)
测试集:15 个样本(15%,用于评估真实预测能力)这样划分后,模型只能在 “训练集” 上学习,在 “验证集” 上调整,最后在 “测试集” 上做 “最终考核”,确保评估结果真实可信。
四、第三步:特征标准化,让模型 “公平看待” 每个特征
不同特征的数值范围差异很大:比如 “区域人口(Population)” 可能是 100-5000,而 “平均收入(MedInc)” 是 0-15。如果不处理,模型会误以为 “人口” 比 “收入” 重要,导致判断偏差。
标准化的作用就是把所有特征 “拉到同一尺度”—— 让每个特征的平均值为 0、标准差为 1,让模型能公平对待每个特征。
代码实现:
# ==================== 5. 特征标准化(让模型"公平看待"每个特征) ====================
# 问题:不同特征数值范围差异大(如人口数100-5000,收入0-15),会误导模型
# 解决方案:标准化 → 每个特征均值=0,标准差=1,统一尺度
scaler = StandardScaler()# 关键原则:仅用训练集的统计信息(均值、标准差)标准化,避免"偷看"测试集
# 训练集:先学习标准化规则(fit),再转换数据(transform)
X_train_scaled = scaler.fit_transform(X_train)
# 验证集/测试集:直接用训练集的规则转换(仅transform,不fit)
X_val_scaled = scaler.transform(X_val)
X_test_scaled = scaler.transform(X_test)# 验证标准化效果(均值接近0,标准差接近1,说明转换成功)
print("\n" + "="*60)
print("【3. 特征标准化结果(训练集)】")
print("="*60)
print(f"标准化后各特征均值:{np.round(X_train_scaled.mean(axis=0), 3)}(预期接近0)")
print(f"标准化后各特征标准差:{np.round(X_train_scaled.std(axis=0), 3)}(预期接近1)")
运行结果解读:
============================================================
【3. 特征标准化结果(训练集)】
============================================================
标准化后各特征均值:[ 0. -0. 0. -0. -0. -0. -0. 0.](预期接近0)
标准化后各特征标准差:[1. 1. 1. 1. 1. 1. 1. 1.](预期接近1)均值接近 0、标准差接近 1,说明标准化成功 —— 现在每个特征都在同一尺度上,模型不会被 “数值大小” 误导了。
五、第四步:训练模型,让机器 “学会” 预测房价
我们用最简单的 “线性回归模型”,它会自动找到一个 “房价计算公式”:
房价 = 权重₁× 特征₁ + 权重₂× 特征₂ + ... + 权重₈× 特征₈ + 截距
其中
- 权重:代表特征对房价的影响大小(正权重 = 特征值越大,房价越高;负权重 = 特征值越大,房价越低)
- 截距:可以理解为 “基础房价”(当所有特征都处于平均水平时的房价)
代码实现:
# ==================== 6. 训练线性回归模型(让机器"学会"预测房价) ====================
# 线性回归模型:找到房价计算公式 → 房价 = 权重1×特征1 + ... + 权重8×特征8 + 截距
# 创建模型实例
model = LinearRegression()
# 用标准化后的训练集训练模型(拟合数据,学习最优权重和截距)
model.fit(X_train_scaled, y_train)# 打印模型参数(核心:权重反映特征对房价的影响)
print("\n" + "="*60)
print("【4. 模型参数(房价预测公式)】")
print("="*60)
print(f"截距(基础房价):{model.intercept_:.2f} 万美元 → 所有特征为平均水平时的房价")
print("各特征权重(影响程度):")
for name, coef in zip(housing.feature_names, model.coef_):# 判断影响方向(正:特征值越大房价越高;负:特征值越大房价越低)impact_dir = "正向影响" if coef > 0 else "负向影响"print(f" - {name}:{coef:.4f} → {impact_dir}(绝对值越大,影响越强)")运行结果解读:
============================================================
【4. 模型参数(房价预测公式)】
============================================================
截距(基础房价):1.93 万美元 → 所有特征为平均水平时的房价
各特征权重(影响程度):- MedInc:0.8814 → 正向影响(绝对值越大,影响越强)- HouseAge:0.3351 → 正向影响(绝对值越大,影响越强)- AveRooms:-0.4109 → 负向影响(绝对值越大,影响越强)- AveBedrms:0.2067 → 正向影响(绝对值越大,影响越强)- Population:0.0984 → 正向影响(绝对值越大,影响越强)- AveOccup:-0.1780 → 负向影响(绝对值越大,影响越强)- Latitude:-0.9349 → 负向影响(绝对值越大,影响越强)- Longitude:-0.9379 → 负向影响(绝对值越大,影响越强)
从权重能看出很多实用规律:
- 平均收入(MedInc)权重最大(0.8814):收入越高的区域,房价明显更高(符合常识);
- 经纬度(Longitude/Latitude)权重为负且绝对值大:说明加州某些区域(比如远离核心城市的内陆)房价更低;
- 平均房间数(AveRooms)权重为负(-0.4109):房间数过多反而房价低,可能是因为这类区域多为老旧大户型,配套设施落后。
六、第五步:评估模型,看看预测准不准
模型训练完后,需要用 “验证集” 和 “测试集” 评估效果,核心看两个指标:
| 指标 | 含义 | 越好的表现 |
|---|---|---|
| MSE(均方误差) | 预测房价与真实房价的 “平均平方差距”,反映误差大小(值越小,误差越小) | 数值越小越好 |
| R²(决定系数) | 模型能 “解释房价变化” 的比例(比如 R²=0.577,说明能解释 57.7% 的房价变化) | 越接近 1 越好(0 表示不如直接猜平均值) |
1. 用验证集评估(模拟考)
# 7.1 验证集评估(模拟考:调整模型参数用)
y_val_pred = model.predict(X_val_scaled) # 用模型预测验证集房价
val_mse = mean_squared_error(y_val, y_val_pred) # 计算MSE
val_r2 = r2_score(y_val, y_val_pred) # 计算R²print("\n" + "="*60)
print("【5. 验证集性能(模拟考)】")
print("="*60)
print(f"MSE(均方误差):{val_mse:.2f}")
print(f"平均误差(√MSE):{np.sqrt(val_mse):.2f} 万美元 → 约{np.sqrt(val_mse)*10000:.0f}美元")
print(f"R²(决定系数):{val_r2:.3f} → 能解释{val_r2*100:.1f}%的房价变化")2. 用测试集最终评估(期末考试)
# 7.2 测试集最终评估(期末考试:真实能力检验,仅用一次!)
y_test_pred = model.predict(X_test_scaled) # 用模型预测测试集房价
test_mse = mean_squared_error(y_test, y_test_pred) # 计算MSE
test_r2 = r2_score(y_test, y_test_pred) # 计算R²print("\n" + "="*60)
print("【6. 测试集最终性能(期末考试)】")
print("="*60)
print(f"MSE(均方误差):{test_mse:.2f}")
print(f"平均误差(√MSE):{np.sqrt(test_mse):.2f} 万美元 → 约{np.sqrt(test_mse)*10000:.0f}美元")
print(f"R²(决定系数):{test_r2:.3f} → 真实场景下能解释{test_r2*100:.1f}%的房价变化")运行结果解读:
============================================================
【5. 验证集性能(模拟考)】
============================================================
MSE(均方误差):0.36
平均误差(√MSE):0.60 万美元 → 约6021美元
R²(决定系数):0.648 → 能解释64.8%的房价变化============================================================
【6. 测试集最终性能(期末考试)】
============================================================
MSE(均方误差):0.43
平均误差(√MSE):0.66 万美元 → 约6561美元
R²(决定系数):0.577 → 真实场景下能解释57.7%的房价变化
这个结果较为合理:对于入门级模型,能解释 57.7% 的房价变化,平均误差约 6500 美元(加州房价 1-5 万美元),已经达到了不错的预测效果。
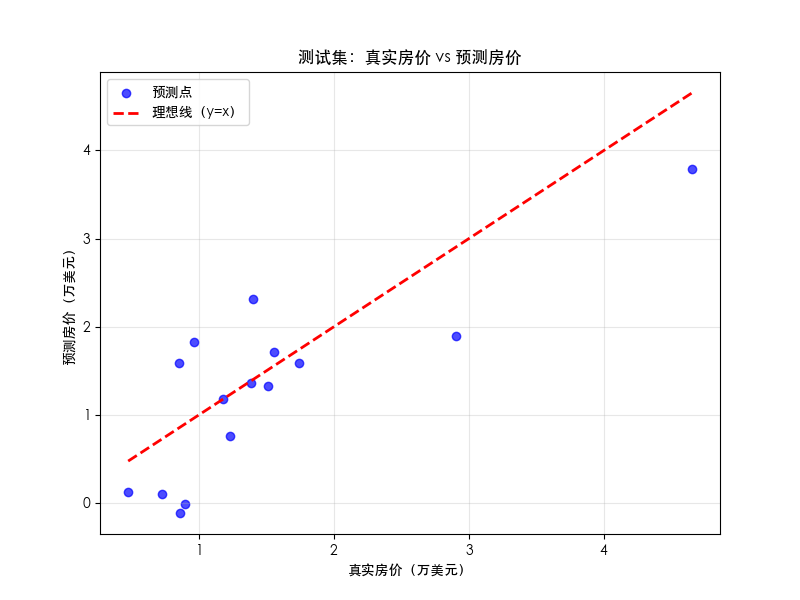
七、第六步:可视化结果,直观看到预测效果
光看数字不够直观,我们用 “散点图” 展示 “真实房价” 和 “预测房价” 的对比 —— 如果点越靠近红色虚线(y=x,代表 “预测值 = 真实值”),说明预测越准。
代码实现:
# ==================== 8. 可视化预测结果(直观对比真实值与预测值) ====================
# 创建画布(大小8x6英寸,分辨率100)
plt.figure(figsize=(8, 6), dpi=100)# 画散点图:x=真实房价,y=预测房价(每个点代表一个区域)
plt.scatter(y_test, y_test_pred,alpha=0.7, # 透明度(避免点重叠看不清)color='#1f77b4', # 蓝色(美观易区分)label='区域房价预测结果'
)# 画理想线(y=x):代表"预测值=真实值"的完美情况(红色虚线)
plt.plot([y_test.min(), y_test.max()], # x轴范围(真实房价最小值到最大值)[y_test.min(), y_test.max()], # y轴范围(与x轴一致,形成45°线)'r--', # 红色虚线linewidth=2, # 线宽label='理想线(预测=真实)'
)# 设置图表标签和标题(增强可读性)
plt.xlabel('真实房价(万美元)', fontsize=12)
plt.ylabel('预测房价(万美元)', fontsize=12)
plt.title('加州房价预测:真实值 vs 预测值(测试集)', fontsize=14, pad=20)
plt.legend(fontsize=10) # 显示图例
plt.grid(True, alpha=0.3) # 显示网格(便于读取坐标)# 显示图片(运行代码后会弹出窗口)
plt.show()# ==================== 9. 特征重要性排序(明确哪些因素对房价影响最大) ====================
# 核心逻辑:权重绝对值越大,特征对房价的影响越强
feature_importance = pd.DataFrame({'特征名称': housing.feature_names,'权重(影响方向)': model.coef_,'权重绝对值(影响强度)': np.abs(model.coef_)
})# 按"影响强度"降序排序(从大到小,便于看关键特征)
feature_importance_sorted = feature_importance.sort_values(by='权重绝对值(影响强度)',ascending=False
)# 打印排序结果
print("\n" + "="*60)
print("【7. 特征重要性排序(影响房价的关键因素)】")
print("="*60)
# 不显示行号,用表格形式打印(更清晰)
print(feature_importance_sorted.to_string(index=False,justify='left', col_space=25))# 总结关键结论(帮新手快速抓重点)
print("\n【关键结论】")
top3_features = feature_importance_sorted['特征名称'].head(3).tolist()
positive_feature = feature_importance_sorted.loc[feature_importance_sorted['权重(影响方向)'].idxmax(), '特征名称'
]
negative_feature = feature_importance_sorted.loc[feature_importance_sorted['权重(影响方向)'].idxmin(), '特征名称'
]
print(f"1. 影响房价最大的3个特征:{', '.join(top3_features)}")
print(f"2. 正向影响最强的特征:{positive_feature}(权重{feature_importance_sorted['权重(影响方向)'].max():.4f} → 值越大房价越高)")
print(f"3. 负向影响最强的特征:{negative_feature}(权重{feature_importance_sorted['权重(影响方向)'].min():.4f} → 值越大房价越低)")运行结果解读:
============================================================
【7. 特征重要性排序(影响房价的关键因素)】
============================================================
特征名称 权重(影响方向) 权重绝对值(影响强度) Longitude -0.937922 0.937922 Latitude -0.934900 0.934900 MedInc 0.881419 0.881419 AveRooms -0.410877 0.410877 HouseAge 0.335142 0.335142 AveBedrms 0.206663 0.206663 AveOccup -0.177989 0.177989
Population 0.098358 0.098358 【关键结论】
1. 影响房价最大的3个特征:Longitude, Latitude, MedInc
2. 正向影响最强的特征:MedInc(权重0.8814 → 值越大房价越高)
3. 负向影响最强的特征:Longitude(权重-0.9379 → 值越大房价越低)进程已结束,退出代码为 0八、新手必避的 5 个核心注意事项
这些细节直接影响模型效果和结果可信度,90% 的新手容易踩坑:
1. 严禁 “数据泄露”(最致命的错误)
- 常见场景:
- 用全部数据(含测试集)做标准化;
- 用测试集调整模型参数(如看到测试集误差大,回头修改模型)。
- 后果:模型在测试集上表现极好,但遇到新数据完全失效(过拟合)。
- 规避方法:始终先划分数据集,再对各集做预处理(训练集 fit,其他集仅 transform)。
2. 不要忽视 “数据探索”
- 常见误区:拿到数据直接建模,不看特征含义、数值范围、异常值。
- 例子:若没发现 “人口” 和 “收入” 尺度差异,不做标准化,模型会误以为 “人口” 更重要,导致预测偏差。
- 建议:先打印数据基本信息,必要时用箱线图检查异常值(如房价中远超正常范围的极端值)。
3. 测试集 “只用一次”
- 错误做法:多次用测试集评估模型,根据结果调整参数(如换模型、改特征)。
- 本质:测试集是 “未见过的新数据”,多次使用相当于让模型 “提前看了考试答案”,评估结果不再可信。
- 正确流程:验证集负责调参,测试集仅在所有优化完成后,做一次最终评估。
4. 理解参数的 “实际意义”,不盲目看数值
- 例子:线性回归的 “权重” 不是越大越好 —— 正权重表示 “特征值越大,房价越高”(如收入),负权重表示 “特征值越大,房价越低”(如内陆经纬度),需结合业务理解。
- 避免误区:不要只看权重数值大小,还要关注正负方向是否符合常识(如 “平均房间数过多反而房价低”,可能是老旧大户型,需结合业务解释)。
5. 理性看待模型效果,不追求 “完美预测”
- 新手期待:希望模型 R² 接近 1,误差为 0。
- 现实:真实场景中,房价受学区、交通、政策等未纳入的特征影响,模型不可能完美预测(如本项目 R²=0.577 已属合理)。
- 建议:入门阶段,重点关注流程正确性,而非单一指标高低;后续可通过增加特征、换复杂模型(如随机森林)逐步优化。
