动态规划题目

背包问题

参考这个讲解的非常生动：https://www.bilibili.com/video/BV1pY4y1J7na/?spm_id_from=333.337.search-card.all.click&vd_source=a671b6c09bdc87f50b8d9fbbf85c6245

题目描述

有若干种物品， 每个物品有重量和价值两个属性， 现在一个有个背包能装的最大的重量是m, 求最多能装的物品的价值总和是多少
如有3个物品， 重量为weights= [2,3,4]， 价值 values=[3,5,6], 有一个背包最大能装的重量为6， 那么能装的最大的价值为 3 + 6=9 （选第一个和第三个物品）

题目解析

可以列出来下面的dp table， 行表示每个物品， 列表示背包容量； dp[i][j] 表示有前i个物品可以选择的情况下，背包最大容量为j的时候，背包能装的最大价值， 如图中dp[2][3] 表示可以选择前两种物品（葡萄和矿泉水）时候，背包容量为3的时候， 能够装的最大值

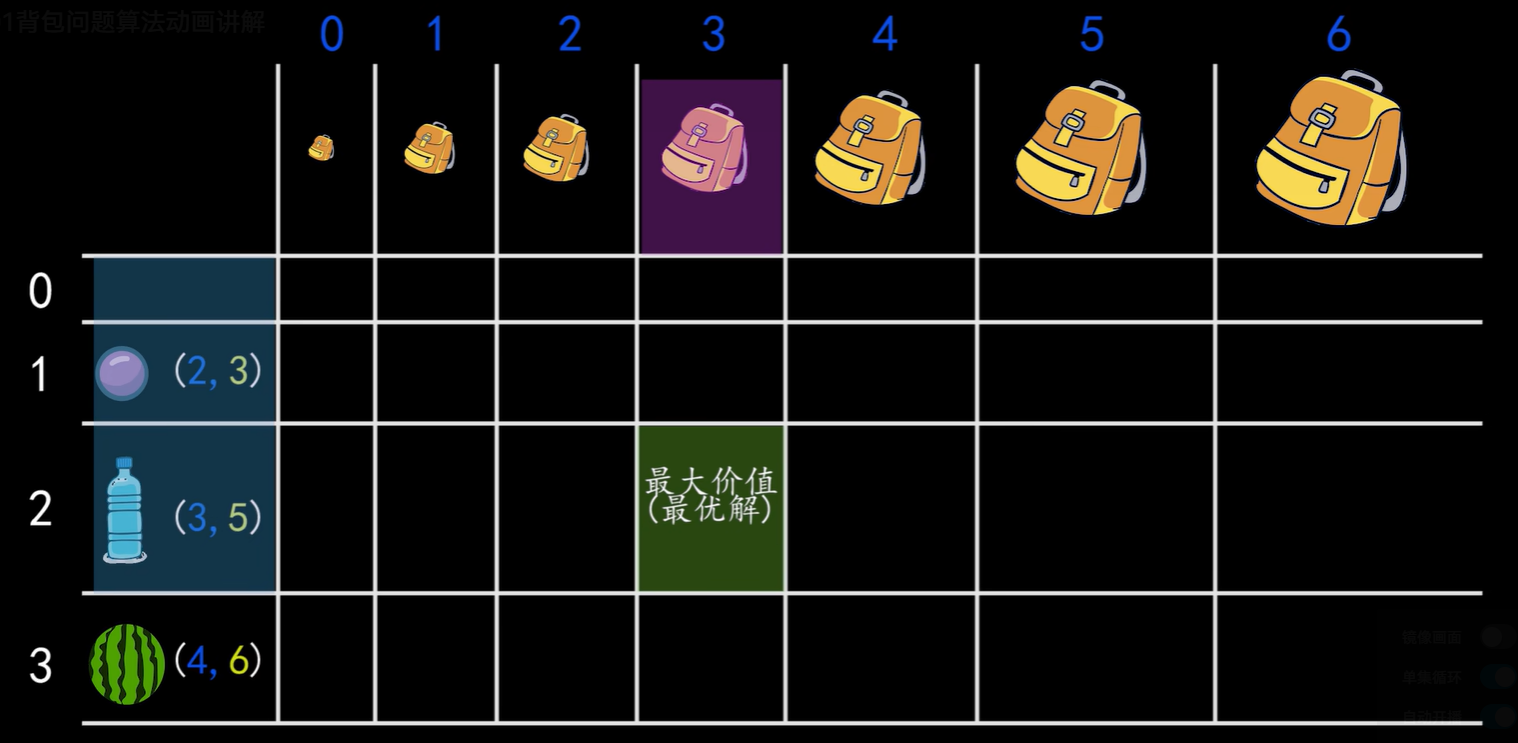
站在当前位置 i,j

1. 如果不选择当前物品：那就是 退化为 前i-1个物品，容量为j 时候 的值， 即 dp[i][j] = dp[i-1][j]
2. 如果选择当前物品：选择当前物品后， 背包容量 就由j 变为了 j-i.weight , 因为选过了当前物品不能再选了，所以退化而为 前i-1个物品，背包容量为 j- i.weight时候的值； 即dp[i][j] = i.val + dp[i-1][j-i.weight] 。（ 如果这里 选过的物品还可以再选择，那还是在当前的i个物品里选择， 即dp[i][j] = i.val + dp[i][j-i.weight] ，这就是完全背包问题 ）
   那么当前位置 要不要选择 第i个物品，就看 这两种情况哪个大了。 总结下来 dp[i][j] = max(dp[i-1][j], i.val + dp[i-1][j-i.weight])
   
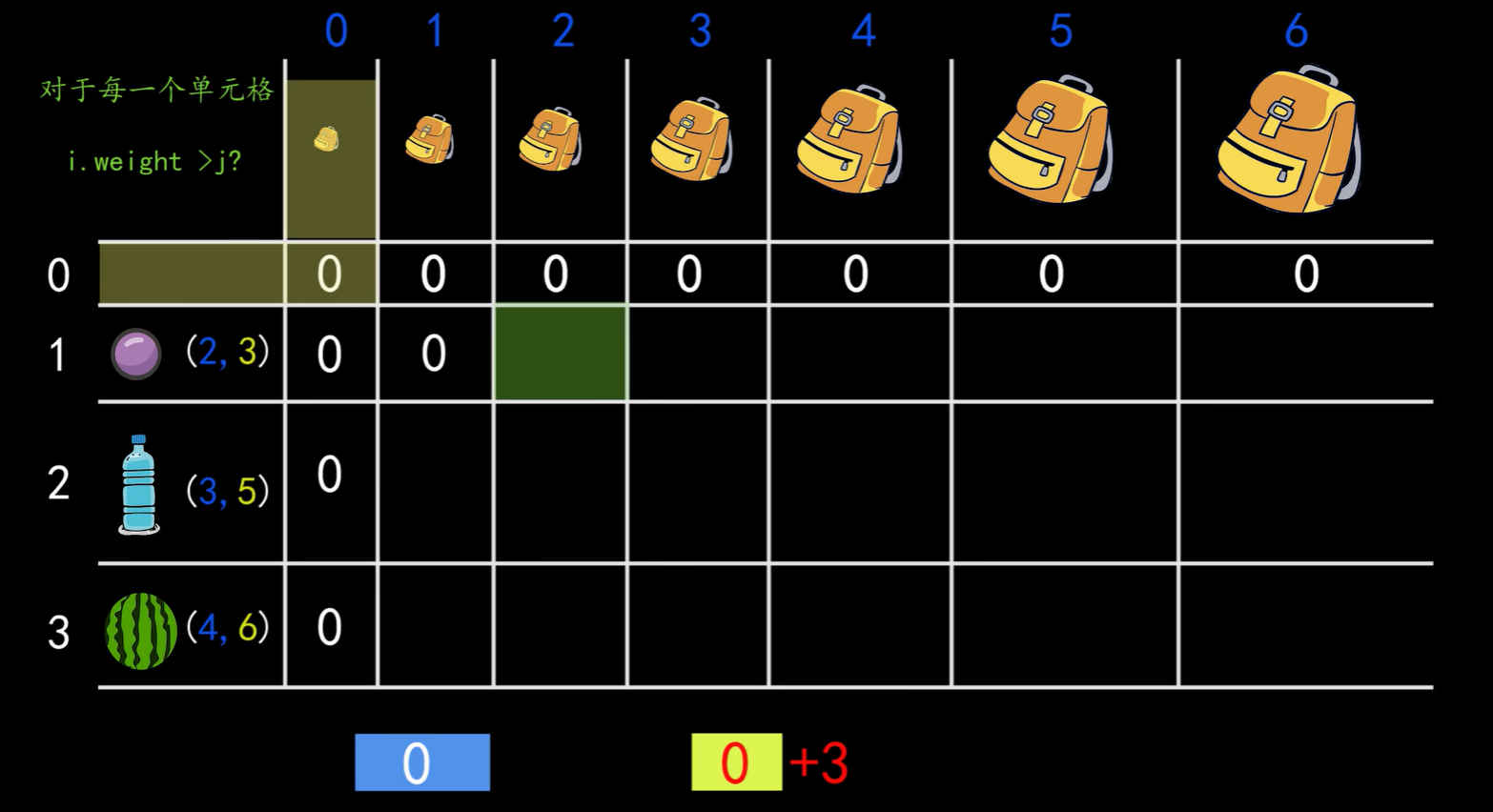
   计算 dp[2][6]
   

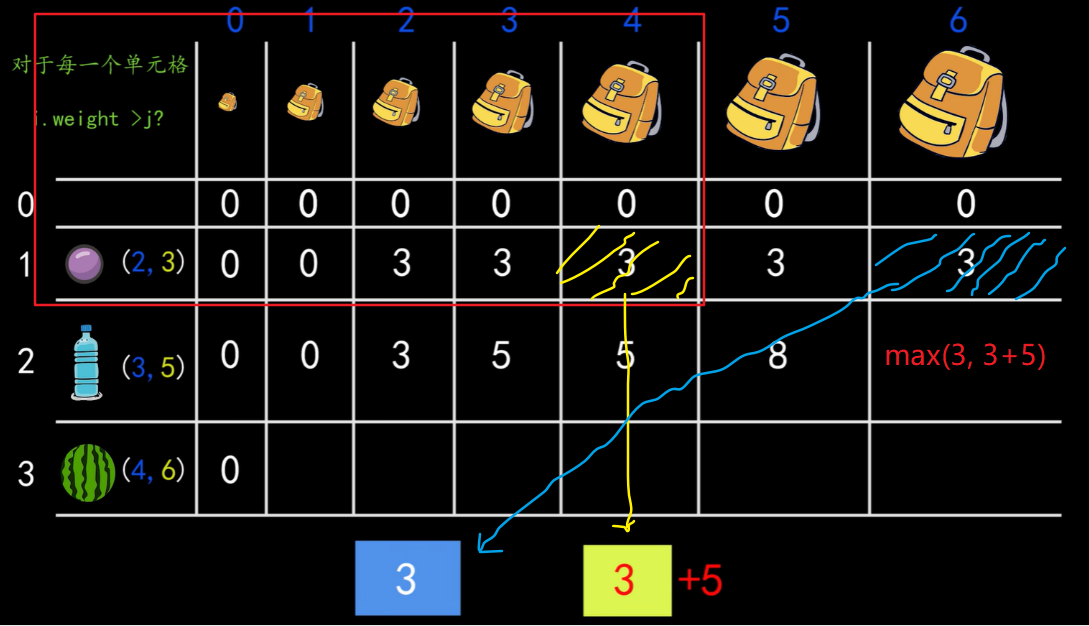
代码

优化为一维dp数组

动态规划求解背包问题时，“最大容量”通常是已知条件。你需要根据问题是01背包（物品唯一）还是完全背包（物品无限），选择合适的​​状态定义​​和​​状态转移方程​​，并注意空间优化后​​遍历顺序​​的区别（01背包逆序，完全背包正序）。核心思想都是通过填充一个 dp表，逐步求解子问题，最终得到全局最优解。

题目

零钱兑换

题目描述

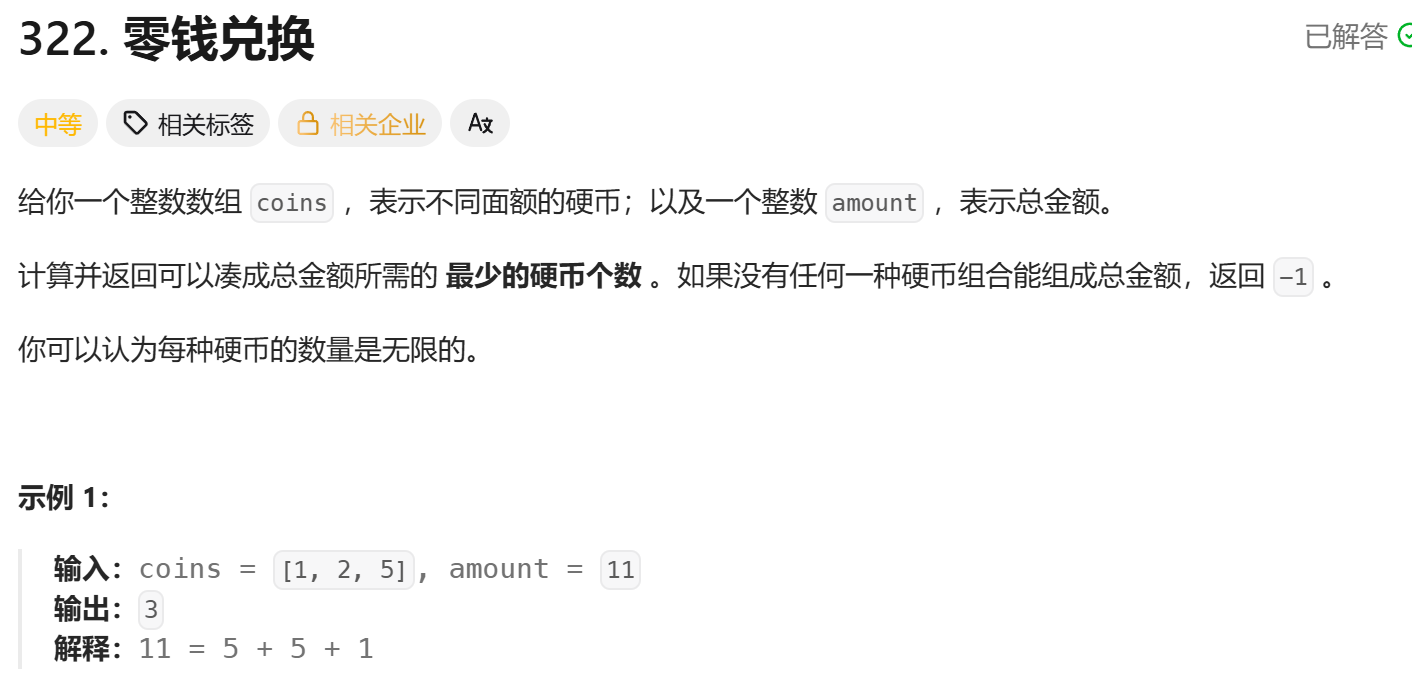
解析过程

背包思维 ：外层循环是coins, 不推荐

N叉树思维：内层循环是coins, 推荐 ； dp[i] = min(dp[i-1], dp[i-2], dp[i-5]) + 1 ， 三种coin可选，相当于三叉树，代码中用遍历coin实现。

代码

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:dp = [float("inf") for i in range(amount+1)]dp[0] = 0for i in range(1,amount+1):for n in coins: # coins=[1,2,15],  dp[11] = min(dp[11-1], dp[11-2], dp[11-15]) + 1if i-n>=0:dp[i] = min(dp[i-n]+1,dp[i])if dp[amount]==float(inf):return -1return dp[amount]

完全平方数

题目解析

不要用二维dp表； 和零钱兑换类似，用N叉树思维
dp[i] = min(dp[i-square1] , dp[i-square2], … 一直到 i <square )

代码

#用动态规划 
class Solution:def numSquares(self, n: int) -> int:dp = [float("inf") for i in range(n+1)] #n+1个无穷大的数 这里可以用数组，也可以用字典dp[0] = 0 # 作为边界条件squares = [i*i for i in range(1,n+1) if (i*i!=0 and i*i <= n)]# print(squares)for i in range(1,n+1):for square in squares:if i < square:break   # 如果i小于square,就跳出循环dp[i] = min(dp[i-square]+1,dp[i])return dp[-1] #返回最后一个数，即为dp[n]

打家劫舍

题目描述

题目解析

相当于求 不相邻的子序列的最大和。
还是定义一个dp数组， 站在i位置，可以选择当前数字， 也可以不选择当前数字

1. 选择当前数字， 那就不能选择i-1数字，退化为 dp[i-2] 问题， dp[i] = dp[i-2] + i.val
2. 不选择当前数字， 退化为 dp[i-1]问题 dp[i] = dp[i-1]
   选择最大的情况

代码

class Solution:def rob(self, nums: List[int]) -> int:dp = [0] * (len(nums)+1) # dp[i] 代表当前共有前i种物品情况下，最大的值为dp[i]dp[1] = nums[0]for i in range(2, len(dp)):dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]) # (1.不选当前的物品，2.选当前的物品,那就要隔一个即i-2)# print(i,' ',dp[i])return dp[-1]

指定长度子序列的乘积和

题目描述

给定一个数组nums， 和一个长度m, 求所有长度为m的子序列的乘积和
如 nums=[1,2,3,6] m=2， 则子序列乘积和为 12 + 13 + 16 + 2 3 + 26 + 36

解析过程

做完了背包问题再来看这道题就非常简单了。显然，对于同一个子序列，一个数字被选中后不能再被重复选了， 属于0-1背包问题
这道题目需要求出来所有的子序列， 并计算乘积， 可以用二维动态规划；一下是dp table

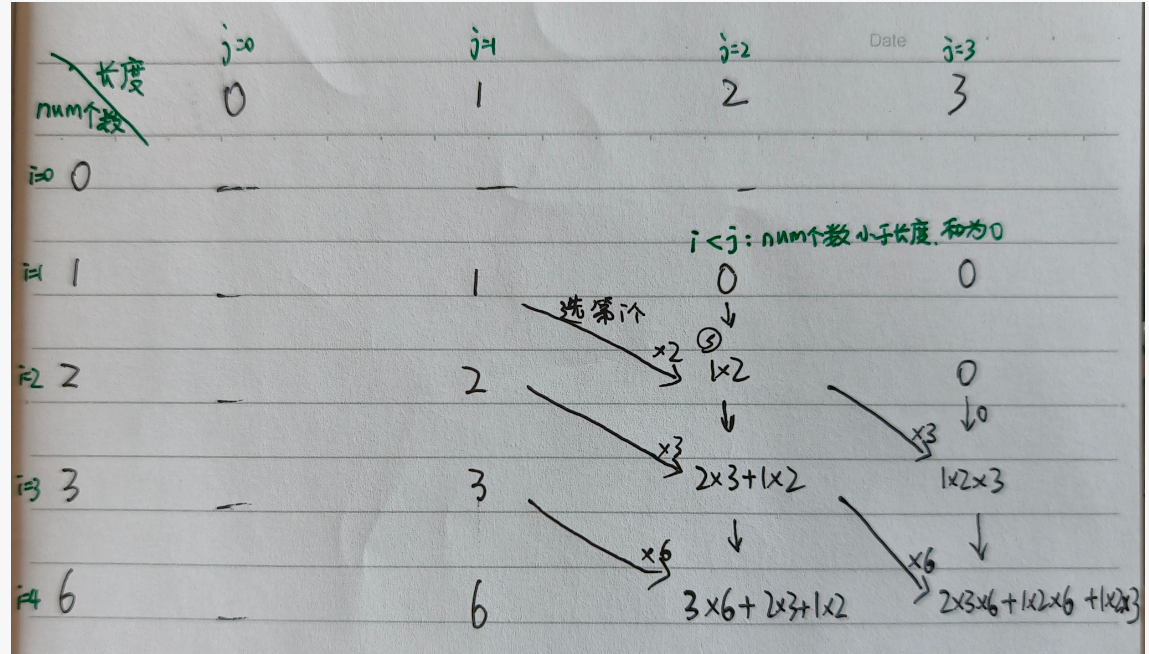
dp[i][j] = dp[i-1][j-1] * i.num + dp[i-1][j]

注意

需要去模运算， 10**9 + 7 , 取模用 %

代码

MOD = 10**9 + 7def product_sum(a, m):n = len(a)# 初始化 dp 表，dp[i][j] 表示考虑前 i 个元素，长度为 j 的子序列的乘积和dp = [[0] * (m + 1) for _ in range(n + 1)]# 初始化：对于所有前 i 个元素，长度为 0 的子序列乘积和为 1（空序列）for i in range(n + 1):dp[i][0] = 1# 动态规划填表for i in range(1, n + 1):        # 考虑前 i 个元素for j in range(1, m + 1):    # 子序列长度 j# 状态转移：不选第 i 个元素 + 选第 i 个元素（乘以 a[i-1]）dp[i][j] = (dp[i-1][j] + a[i-1] * dp[i-1][j-1]) % MODreturn dp[n][m]# 测试用例
if __name__ == "__main__":print(product_sum([1, 2, 3], 2))   # 输出应为 11print(product_sum([2, 3, 4, 5], 3)) # 输出应为 154[2](@ref)

最长递增子序列

题目描述

解析过程

代码

class Solution:def lengthOfLIS(self, nums: List[int]) -> int:# 0: 以nums[0]=10结尾的最长递增子序列: 10， 长度为1# 1: 以nums[1]=9 , 找小于9的，没有，那就只选择9，长度为1# 2: 找小于2的，没有， 那就只选择2，长度为1# 3: 找小于5的，有 2，1 + 1=2# 找小于3的，2， 1+1 = 2# 找小于7的，2，5，3  max（1,2,2）+1 = 3# 找小于101的，3+1=4# 找小于18的，3+1=4res = 1dp = [1] * len(nums) # 以nums[i]结尾的最长递增子序列for i in range(len(nums)):for j in range(i):if nums[j] < nums[i]: # 遍历找到小于当前数的前面的所有的数， 最长的+1 即为当前结尾的最长子序列dp[i] = max(dp[i], dp[j] + 1) # res = max(res, dp[i])return res

最长公共子序列

题目描述

解析过程

注意点

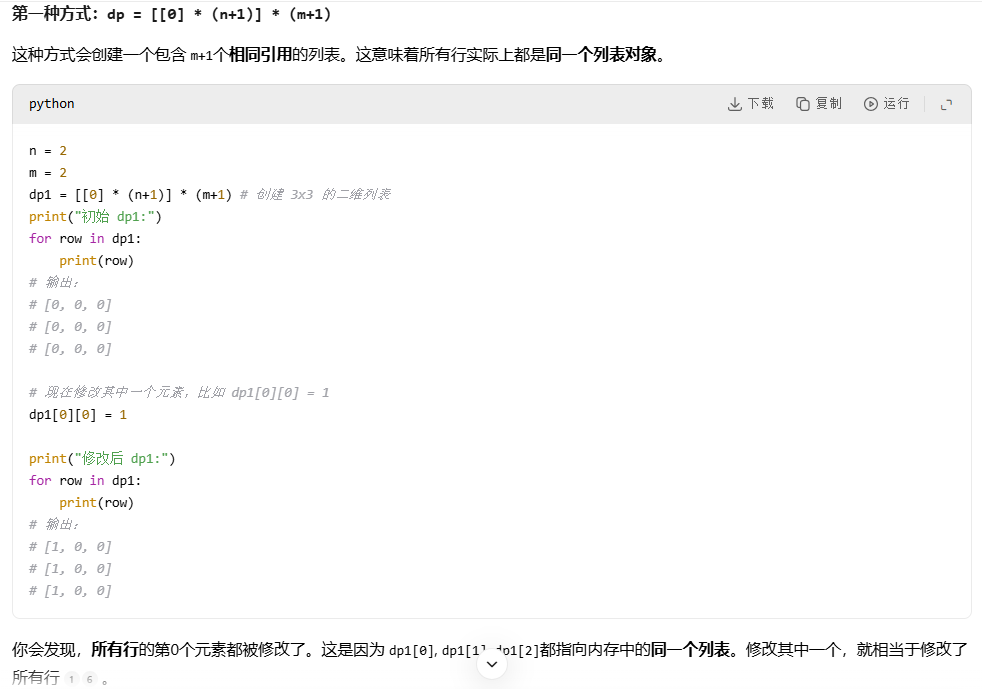
代码

class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:m = len(text1)n = len(text2)# dp = [[0]* (n+1)] *( m + 1) # 注意： 这种方式初始化是错误的，每一行修改都会dp = [[0] * (n + 1) for _ in range(m + 1)] # 使用 列表推导式初始化print(m)print(n)for i in range(1, m+1):for j in range(1, n + 1):t1, t2 = text1[i-1], text2[j-1]if t2==t1:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])# print(f'{i}_{j}:', dp[i][j])return dp[m][n]

最大子数组和

题目描述

题目解析

考虑 以dp[i]结尾的最大和连续子数组，那么站在当前位置， 可以选择 当前位置的数 和前面的子数组拼起来组成一个子数组， 也可以 另起山头，自己作为一个子数组的开始。 选二者最大的即可。
dp[i] = max(dp[i-1] + i.val , i.val)

最终的结果就是 dp[i]里面的最大值。

代码

class Solution:def maxSubArray(self, nums: List[int]) -> int:dp = [0]* (len(nums)+1)res = -float('inf')for i in range(1, len(dp)):dp[i] = max(dp[i-1]+nums[i-1], nums[i-1])res = max(dp[i], res)# print(dp[i])return res