【LeetCode热题100道笔记】二叉树的层序遍历
题目描述
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
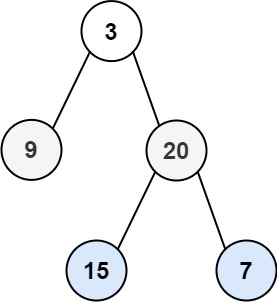
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
思考:基础BFS实现(队列存储整层节点)
核心是用队列维护当前层节点,每次遍历完当前层所有节点后,收集下一层节点,循环直至队列为空。
算法过程
- 边界处理:若根节点
root为null(空树),直接返回空数组。 - 初始化:创建结果数组
result(存储每层节点值),队列queue初始存入根节点(第一层仅根节点)。 - 层序循环(遍历每一层):
- 收集当前层值:将队列中所有节点的
val提取为子数组,加入result; - 收集下一层节点:创建临时数组
tmp,遍历当前层所有节点,若节点有左/右子节点,依次加入tmp; - 更新队列:将队列替换为
tmp(下一层节点),进入下一轮循环,直至队列为空。
- 收集当前层值:将队列中所有节点的
- 返回结果:返回
result,即按层排列的节点值二维数组。
时空复杂度
- 时间复杂度:O(n),n为二叉树节点总数。
原因:每个节点仅入队、出队各1次,提取节点值的操作也为O(n),总操作次数与节点数线性相关。 - 空间复杂度:O(m),m为二叉树最宽层的节点数。
原因:队列需存储当前层所有节点,最坏情况(完全二叉树最后一层)m=O(n/2)=O(n),最好情况(链状树)m=1。
基础代码
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {if (!root) return []; // 空树直接返回const result = []; // 存储最终层序结果let queue = [root]; // 队列:维护当前层节点while (queue.length) {// 1. 收集当前层所有节点的valresult.push(queue.map(node => node.val));// 2. 收集下一层节点(左子节点优先)let tmp = [];for (let node of queue) {if (node.left) tmp.push(node.left);if (node.right) tmp.push(node.right);}// 3. 切换到下一层queue = tmp;}return result;
};
思考:优化BFS实现(单队列+指针避免临时数组)
基础实现中,每次收集下一层节点需创建临时数组tmp,优化思路是用“队列指针”标记当前层边界:通过front指针记录已处理的节点位置,计算当前层节点数,直接在原队列中遍历当前层、添加下一层节点,避免临时数组开销。
算法过程
- 边界处理:同基础实现,空树返回空数组。
- 初始化:结果数组
ret,队列q初始存入根节点,front指针初始为0(标记队列中未处理节点的起始位置)。 - 层序循环(按指针控制层边界):
- 计算当前层节点数:当前层节点数 = 队列总长度 -
front(排除已处理的上层节点); - 初始化当前层子数组:在
ret中新增一个空数组,用于存储当前层节点值; - 遍历当前层节点:循环
currentLevelSize次:- 取队列中
front位置的节点(当前待处理节点),front指针后移(标记为已处理); - 将节点
val加入ret的最后一个子数组(当前层); - 若节点有左/右子节点,直接加入队列尾部(下一层节点);
- 取队列中
- 计算当前层节点数:当前层节点数 = 队列总长度 -
- 返回结果:返回
ret。
时空复杂度
- 时间复杂度:O(n),与基础实现一致,每个节点仅处理1次。
- 空间复杂度:O(m),与基础实现一致(队列存储节点数不变),但减少了临时数组
tmp的额外空间(基础实现的tmp最多存储m个节点,优化后直接复用原队列,空间更紧凑)。
优化代码
/*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val = (val===undefined ? 0 : val)* this.left = (left===undefined ? null : left)* this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number[][]}*/
var levelOrder = function(root) {const ret = [];if (!root) return ret;const q = [root]; // 单队列存储所有待处理节点let front = 0; // 指针:标记已处理节点的边界while (front < q.length) {// 1. 计算当前层节点数(队列中未处理的节点数)const currentLevelSize = q.length - front;// 2. 初始化当前层子数组ret.push([]);// 3. 遍历当前层所有节点for (let i = 0; i < currentLevelSize; i++) {const node = q[front++]; // 取当前节点,指针后移(O(1)操作)ret[ret.length - 1].push(node.val); // 存入当前层值// 4. 下一层节点直接加入队列尾部if (node.left) q.push(node.left);if (node.right) q.push(node.right);}}return ret;
};
基础实现与优化实现对比
| 维度 | 基础实现 | 优化实现 |
|---|---|---|
| 核心逻辑 | 队列存当前层,临时数组存下一层 | 单队列+指针,标记层边界 |
| 空间开销 | 需额外临时数组tmp | 复用原队列,无临时数组 |
| 时间效率 | O(n) | O(n)(操作更紧凑) |
| 代码复杂度 | 简单直观 | 需理解指针与层边界关系 |
适用场景:
- 基础实现适合代码简洁性优先的场景,逻辑易理解;
- 优化实现适合空间敏感场景,尤其在节点数较多时,可减少临时数组的内存占用。
