当前位置：首页 > news >正文

数据结构之【哈希的相关概念】

news 2025/9/5 11:24:40

1.哈希及哈希表的概念

3.哈希冲突

2.哈希函数

(1) 哈希函数设计原则：

(2)哈希函数作用是：

(3)常见的哈希函数

4.哈希冲突解决

(1)闭散列

线性探测

二次探测

(2)开散列

1.哈希及哈希表的概念

哈希又叫做散列，是一种通过哈希函数将任意大小的数据（如字符串、数字等）映射为固定大小的哈希值的技术

哈希表是一种基于哈希技术(通过哈希函数将关键码映射到存储位置)实现的数据结构，插入、删除和查找操作高效（平均时间复杂度为 O(1)）

用该方法进行搜索不必进行多次关键码的比较，因此搜索的速度比较快

问题：按照上述哈希方式，向集合中插入元素44，会出现什么问题？

3.哈希冲突

哈希冲突是一种不同的元素，通过相同的哈希函数而产生相同的哈希地址的现象

插入元素44所计算的哈希地址与插入元素4时所计算的哈希地址相同，这就是哈希冲突现象

哈希冲突是不能杜绝的

把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”

2.哈希函数

好的哈希函数可以减少冲突的概率，但是不能够绝对避免

(1) 哈希函数设计原则：

1哈希函数应该尽可能简单

2.哈希函数的定义域必须包括需要存储的全部关键码，而

如果散列表允许有m个地址时，哈希函数的值域必须在0到m-1之间

4. 哈希函数的值域应该尽可能均匀分布，即取每个位置应该是等概率的

(2)哈希函数作用是：

建立元素与其存储位置之间的对应关系，在存储元素时，先通过哈希函数计算元素在哈希表格中的存储位置，然后存储元素。

(3)常见的哈希函数

直接定址法

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B

优点：简单、均匀缺点：需要事先知道关键字的分布情况

使用场景：适合查找比较小且连续的情况

除留余数法

设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，

按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址

还有平方取中法(了解) 随机数法(了解) 数字分析法(了解) 叠加法(了解) 等

4.哈希冲突解决

好的处理哈希冲突的方法比较关键，因为冲突处理不当，会增加后序元素冲突的概率

解决哈希冲突两种常见的方法是：闭散列和开散列

(1)闭散列

闭散列也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去

寻找下一个空位置的方式有线性探测和二测探测

线性探测

从发生冲突的位置开始，依次向后探测，直到寻找到空位置为止

插入某元素时，通过哈希函数获取待插入元素在哈希表中的位置如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突，使用线性探测找到下一个空位置，插入新元素

删除某元素时，我们不能将该元素置为所谓的"无效值"，因为无效值究竟是多少？0？万一插入的值就是0呢。

解决方法是：标记存储元素的状态 EXIST(存在) DELETE(删除) EMPTY(空)

这样，插入一个元素时，同时标记(EXIST)当从哈希表中删除某个元素时，并没有将该元素真正的删除掉，而是采用标记(DELETE)的方式处理但是不能直接将该位置标记为空，否则会影响从该位置产生冲突的元素的查找(与查找的结束条件有关)

查找某一个元素时，我们先通过哈希函数找到对应的哈希地址，但是由于哈希冲突与线性探测解决方式的可能，如果当前位置找不到，我们就会从冲突位置开始向后寻找该元素

因为要插入的值会存放在从冲突位置开始向后的第一个EMPTY位置，那么查找时一定是遇到第一个EMPTY位置就停止(结束条件解释了删除元素时不能标记为EMPTY而是DELETE)

线性探测优点：实现非常简单

线性探测缺点：一旦发生哈希冲突，所有的冲突连在一起，容易产生数据“堆积”，即：不同关键码占据了可利用的空位置，使得寻找某关键码的位置需要许多次比较，导致搜索效率降低

二次探测

线性探测由于是从冲突位置向后依次寻找下一个空位置，那么数据就容易堆积，二次探测就是对寻找方式的改进：

hashi = ( hashi_0 + i^2) % m 或 hashi = ( hashi_0 - i^2) % m 其中：i = 1,2,3......

hashi_0 是通过哈希函数Hash(x)对元素的关键码 key 进行计算得到的位置，m是表的大小

研究表明：当表的长度为质数且表装载因子a不超过0.5时，新的表项一定能够插入，而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置，就不会存在表满的问题。在搜索时可以不考虑表装满的情况，但在插入时必须确保表的装载因子a不超过0.5，如果超出必须考虑增容

闭散列最大的缺陷就是空间利用率比较低，这也是哈希的缺陷

(2)开散列

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链 接起来，各链表的头结点存储在哈希表中

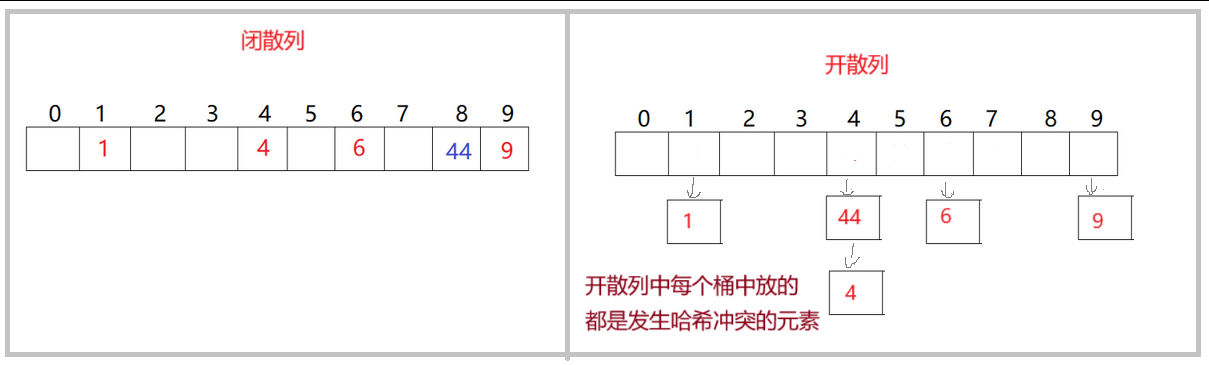
若使用除留余数法计算哈希地址，并不是所有的关键码都是整型，还可能是字符串等

这就可以使用仿函数进行解决(下一期博客模拟实现时具体讲解)

桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容

策略	开放定址法（Open Addressing）	链地址法（Separate Chaining）
核心思想	冲突时，在哈希表中寻找下一个空闲位置（探测序列）存储元素。	冲突时，将元素存储在对应桶的链表（或树）中。
存储结构	数组（固定大小，可能扩容）。	数组 + 链表（或动态数组、红黑树等）。
冲突扩散	易产生“聚集”，导致连续冲突。	冲突仅影响当前桶，不会扩散。