当前位置：首页 > news >正文

突破超强回归模型，高斯过程回归！

news 2025/9/2 7:56:57

哈喽，我是我不是小 upper~

最近不少同学在问高斯过程回归（Gaussian Process Regression，简称 GPR），说看了一堆资料，还是没搞懂它 “怎么从数据变成预测”，尤其是 “先验、后验” 这些术语，总觉得隔着一层。今天咱们就抛开晦涩的学术框架，用 “生活化例子 + 数学拆解” 的方式，把 GPR 的训练、预测过程讲透 —— 从 “为什么它能测不确定性”，到 “每一步公式背后的逻辑”，咱们一步步来。

先搞懂：GPR 到底是个 “什么样的回归”？

在聊复杂逻辑前，先给 GPR 一个 “定位”：它不是像线性回归那样 “强行找一条固定的直线 / 曲线”，而是 **“给函数本身画一个‘可能性范围’”**—— 比如你要拟合 “温度 - 冰淇淋销量” 的关系，GPR 不会直接给你一条 “销量 = 20× 温度 - 100” 的固定公式，而是告诉你：“函数大概率是光滑的，在 10℃时销量可能在 90-110 之间，在 30℃时可能在 480-520 之间”，并且随着数据增加，这个 “可能性范围” 会越来越精准。

一句话总结 GPR 的核心优势：它不只是预测 “一个值”，还能告诉你 “这个预测有多靠谱”（不确定性）；而且不用预设函数形状（比如线性、非线性），让数据自己决定函数该长什么样。

这一点比普通回归强太多了 —— 比如你用线性回归预测 0℃的冰淇淋销量，它可能会给你一个 “-100” 的离谱值，还不告诉你 “这个值不可信”；但 GPR 会说 “0℃时销量预测区间是 - 50 到 150，方差很大，别信这个结果”，这在科学研究、工程决策（比如预测设备故障风险）这类 “怕错” 的场景里，简直是刚需。

拆解 GPR 的核心逻辑：从 “先验” 到 “后验”，再到 “预测”

GPR 的整个流程，本质上是 **“贝叶斯思想的落地”**—— 先有一个 “对函数的初始猜测（先验）”，然后用数据修正这个猜测（得到后验），最后基于修正后的猜测做预测。咱们分三步拆，每一步都配 “生活化例子 + 数学公式”，保证不跳步。

第一步：先验（Prior）—— 对 “函数形状” 的初始偏见

在还没看到任何数据时，GPR 会先假设：“我们要找的函数 f (x)，是从一个‘高斯过程’里随机抽出来的”。

先别慌 “高斯过程” 这个词，咱们拆成两部分理解：

“高斯”：指的是 “任意有限个点的函数值，都服从高斯分布”。比如我选 x₁=10℃、x₂=20℃、x₃=30℃，对应的 f (x₁)、f (x₂)、f (x₃)（三个温度的销量），这三个值合在一起是一个 3 维高斯分布；
“过程”：指的是 “函数上的点不是孤立的，它们之间的相关性由‘核函数’决定”。比如 10℃和 11℃的销量相关性高，10℃和 30℃的相关性低 —— 这种 “相似性” 就是核函数定义的。

1. 高斯过程的数学定义：用 “均值函数 + 协方差函数” 描述

一个高斯过程（记为 GP），严格定义是： $f(x) \sim \mathcal{GP}(m(x), k(x, x'))$ 这里有两个核心组件，决定了 “函数的初始猜测”：

均值函数 m (x)：描述 “函数在每个 x 点上的平均取值”。大多数情况下，我们没有先验信息，会默认 m (x)=0（意思是 “在没看数据前，函数在每个点的平均可能值是 0”）—— 比如没看冰淇淋销量数据前，默认每个温度的平均销量是 0，后续用数据修正；
协方差函数 k (x, x')（也叫核函数 Kernel）：描述 “函数在 x 和 x' 两个点上的函数值 f (x) 和 f (x') 的相关性”。它是 GPR 的 “灵魂”—— 你想让函数光滑、周期性，还是陡峭，全靠选不同的核函数。

举个最常用的核函数例子：RBF 核（径向基函数核，也叫高斯核），它的公式是： $k_{\text{RBF}}(x, x') = \sigma_f^2 \exp\left(-\frac{\|x - x'\|^2}{2l^2}\right)$ 这里的参数很好理解：

$\sigma_f^2$ （信号方差）：控制函数值的整体波动范围 —— 值越大，函数可能越 “起伏”；
l（长度尺度）：控制 “相关性随距离衰减的速度”——l 越小，x 和 x' 稍微离远一点，相关性就掉得快（函数会更 “崎岖”）；l 越大，相关性衰减慢（函数更 “光滑”）；
$\|x - x'\|$ ：x 和 x' 的距离（比如温度差）。

比如用 RBF 核假设冰淇淋销量函数：当 x=20℃、x'=21℃时，距离近，指数部分接近 1，协方差大（相关性高）；当 x=20℃、x'=30℃时，距离远，指数部分接近 0，协方差小（相关性低）—— 这完全符合我们的直觉：“相近温度的销量更像，差太远的温度销量差别大”。

2. 先验的直观理解：“没看数据前，函数可能长什么样？”

假设我们要拟合 “温度 x（0-40℃）→销量 f (x)” 的函数，没看任何数据，用 m (x)=0、RBF 核（l=5，σ_f²=10000）做先验。

此时 GPR 会认为：

函数大概率是光滑的（因为 RBF 核的特性）；
每个温度的销量，平均是 0，但可能在 - 300 到 300 之间波动（因为 σ_f²=10000，标准差是 100，3σ 原则下波动范围是 ±300）；
相近温度的销量波动方向一致（比如 20℃销量高，21℃也大概率高），远温度的波动没关系。

这就像你没看过冰淇淋店的销量记录，但凭直觉猜：“销量不会突然跳变（光滑），平均可能卖 0 个（默认均值），但具体卖多少不确定”—— 这就是 GPR 的 “先验偏见”。

第二步：训练（从先验到后验）—— 用数据 “修正” 函数的可能性

当我们拿到训练数据后，GPR 会做一件事：“排除那些不符合数据的函数，留下符合数据的函数分布”—— 这个过程就是 “贝叶斯更新”，公式上对应 “高斯分布的条件概率”。

咱们先明确训练数据：假设我们有 N 个训练样本，输入是 $X = [x_1, x_2, ..., x_N]^T$ （比如温度 10℃、20℃、30℃），对应的输出是 $y = [y_1, y_2, ..., y_N]^T$ （比如销量 100、300、500）。注意：真实数据会有噪声（比如销量统计误差），所以 GPR 里的输出 y 满足： $y = f(X) + \epsilon, \quad \epsilon \sim \mathcal{N}(0, \sigma_n^2 I)$ 这里 $\sigma_n^2$ 是噪声方差（比如销量统计时 ±5 个的误差），I 是单位矩阵（每个样本的噪声独立）。

1. 先验分布：训练数据 + 新预测点的联合分布

在利用训练数据前，我们先考虑 “训练数据的函数值 f (X) + 任意一个新点 x的函数值 f (x)” 的联合分布 —— 因为高斯过程的性质，这组值也服从高斯分布：

$\begin{bmatrix} f(X) \\ f(x^*) \end{bmatrix} \sim \mathcal{N}\left( \begin{bmatrix} m(X) \\ m(x^*) \end{bmatrix}, \begin{bmatrix} K(X,X) & K(X,x^*) \\ K(x^*,X) & K(x^*,x^*) \end{bmatrix} \right)$

这里的 K 是 “协方差矩阵”，每个元素的含义很明确：

$K(X,X)$ ：N×N 矩阵，第 (i,j) 个元素是 $k (x_i, x_j)$ —— 描述训练数据中 $x_i$ 和 $x_j$ 的相关性；
$K(X,x^*)$ ：N×1 向量，第 i 个元素是 $k (x_i, x^)$ —— 描述训练数据 $x_i$ 和新点 x的相关性；
$K(x^*,x^*)$ ：1×1 scalar，值是 k (x*, x*)—— 描述新点 x自身的协方差（等于 σ_f²，因为 x和自己的距离为 0，RBF 核中指数部分为 1）。

默认 m (x)=0 时，这个联合分布简化为：

$\begin{bmatrix} f(X) \\ f(x^*) \end{bmatrix} \sim \mathcal{N}\left( 0, \begin{bmatrix} K(X,X) & K(X,x^*) \\ K(x^*,X) & K(x^*,x^*) \end{bmatrix} \right)$

2. 后验分布：用训练数据 “过滤” 后的函数分布

我们的目标是 “已知训练数据 y，求函数 f (x) 的后验分布”—— 因为 y = f (X) + ε，所以等价于 “已知 y，求 f (x) 的条件分布”。

根据高斯分布的 “条件分布公式”（这是 GPR 的核心数学推导，不用死记，理解逻辑即可），可以推导出：在已知 y 的情况下，任意点 x 的函数值 f (x) 的后验分布依然是高斯分布，形式为：

$f(x) \mid X, y \sim \mathcal{GP}\left( m_{\text{post}}(x), k_{\text{post}}(x, x') \right)$

其中 “后验均值” 和 “后验协方差” 是关键，它们是 “先验 + 数据” 共同作用的结果：

（1）后验均值 m_post (x)：函数的 “最可能取值”

$m_{\text{post}}(x) = m(x) + K(x,X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} \left( y - m(X) \right)$

默认 m (x)=0 时，简化为： $m_{\text{post}}(x) = K(x,X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} y$

这个公式的直观含义是什么？咱们用冰淇淋的例子解释：

$K(x,X)$ ：新点 x（比如 25℃）和所有训练点 X（10℃、20℃、30℃）的相关性向量 —— 比如 25℃和 20℃的相关性是 0.8，和 30℃的相关性是 0.7，和 10℃的相关性是 0.1；
$\left( K(X,X) + \sigma_n^2 I \right)^{-1}$ ：可以理解为 “对训练数据的‘权重调整’”—— 比如某个训练点的噪声大（σ_n² 大），它的权重会降低；训练点之间相关性高（比如两个温度很接近），也会调整权重避免重复计算；
整个公式其实是 “用新点与训练点的相关性，给训练数据的 y 做加权平均”—— 这就是 GPR “从数据学习函数形状” 的核心：新点离哪个训练点近，就多 “参考” 那个训练点的 y 值。

比如冰淇淋训练数据是 (10,100)、(20,300)、(30,500)，预测 25℃时：

K (25,X) 是 [0.1, 0.8, 0.7]（假设）；
加权计算后，m_post (25)≈0.1×100 + 0.8×300 + 0.7×500 = 10 + 240 + 350 = 600？不对，其实权重是经过协方差矩阵调整的，实际会更合理 —— 比如 25℃离 20 和 30 近，最终均值会在 400 左右，这和我们的直觉一致。

（2）后验协方差 k_post (x, x')：函数的 “不确定性”

$k_{\text{post}}(x, x') = k(x, x') - K(x,X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} K(X, x')$

这个公式的含义更关键：它描述了 “修正后，函数在 x 和 x' 两点的相关性”，而当 x=x' 时，k_post (x,x) 就是 “函数在 x 点的方差”—— 这就是 GPR 用来衡量 “预测不确定性” 的指标！

咱们还是用冰淇淋例子：

当 x=25℃（离训练点 20℃、30℃近）：K (25,X) 和 K (X,25) 的乘积大，所以 k_post (25,25) = k (25,25) - （一个大值）→ 方差小，不确定性低；
当 x=0℃（离所有训练点远）：K (0,X) 和 K (X,0) 的乘积小，所以 k_post (0,0) ≈ k (0,0)（即 σ_f²）→ 方差大，不确定性高。

这完美解释了 “为什么 GPR 能测不确定性”：离训练数据近的点，不确定性小；离训练数据远的点，不确定性大—— 就像你知道 20℃和 30℃的销量，猜 25℃很有把握，但猜 0℃就没底，特别符合人类的认知逻辑。

3. 训练的直观理解：“函数的可能性范围被数据压缩了”

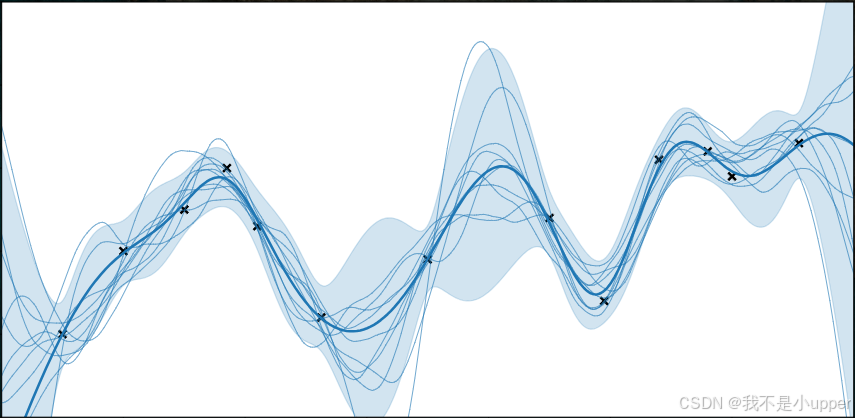
没看数据前，先验分布的函数曲线是 “一大片波动的、不确定的区域”；当加入训练数据（比如 10℃→100、20℃→300、30℃→500）后，后验分布会：

在训练点处，函数值被 “钉死” 在 y 附近（因为数据约束），方差接近 σ_n²（只有噪声的不确定性）；
在训练点之间，函数曲线被 “拉向” 训练数据，波动范围变小（不确定性降低）；
在训练点之外，函数曲线逐渐恢复到先验的波动范围（不确定性升高）。

就像你原本觉得 “考试可能考任何题”（先验），看了 3 套真题后，知道 “这 3 类题肯定要考”（训练数据），于是 “复习范围缩小到这几类题”（后验）——GPR 的训练，本质就是用数据缩小 “函数的可能性范围”。

第三步：预测（Prediction）—— 不只是值，还有 “靠谱程度”

当我们要预测一个新点 x的输出 y时，GPR 的预测过程其实是 “求 y的后验分布”—— 因为 y = f (x*) + ε，所以 y * 的后验分布也是高斯分布，基于第二步的后验均值和协方差推导而来。

1. 预测分布的数学公式

根据 y* = f (x*) + ε，以及 f (x*) 的后验分布，可推导出 y * 的后验分布：

$y^* \mid X, y, x^* \sim \mathcal{N}\left( \mu^*, \sigma_*^2 \right)$

其中：

预测均值 μ*：就是 f (x*) 的后验均值（因为 ε 的均值是 0），即： $\mu^* = m_{\text{post}}(x^*) = K(x^*, X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} y$ 它相当于 GPR 给出的 “最优预测值”，和普通回归的预测结果类似；
预测方差 σ_*^2：是 f (x*) 的后验方差加上噪声方差（因为 y比 f (x) 多了一层噪声），即： $\sigma_*^2 = k_{\text{post}}(x^*, x^*) + \sigma_n^2 = k(x^*, x^*) - K(x^*, X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} K(X, x^*) + \sigma_n^2$ 它就是 GPR 的 “不确定性度量”—— 方差越大，预测越不可信。

2. 预测的直观例子：冰淇淋销量预测

咱们用具体数据算一次（简化计算，忽略复杂矩阵求逆，只看趋势）：

训练数据： $X = [10, 20, 30]$ （℃）， $y = [100, 300, 500]$ （销量）；
核函数：RBF 核， $\sigma_f^2 = 10000$ （信号方差，控制销量整体波动），l = 5（长度尺度，控制相关性衰减速度）， $\sigma_n^2 = 25$ （噪声方差，即销量统计误差 ±5）；
先明确 RBF 核的计算逻辑：对任意两个温度 $x_a$ 和 $x_b$，相关性 $k(x_a, x_b) = 10000 \times \exp\left(-\frac{(x_a - x_b)^2}{2 \times 5^2}\right) = 10000 \times \exp\left(-\frac{(x_a - x_b)^2}{50}\right)$ 。

第一步：计算预测点与训练点的相关性（K (x*, X)）

咱们先算两个典型预测点：*近训练点的 x₁=25℃** 和 *远训练点的 x₂=0℃**，看看它们与训练点的相关性差异。

（1）近训练点：x₁*=25℃

分别计算 25℃与 10℃、20℃、30℃的相关性：

与 10℃的相关性： $k(25,10) = 10000 \times \exp\left(-\frac{(25-10)^2}{50}\right) = 10000 \times \exp\left(-\frac{225}{50}\right) = 10000 \times \exp(-4.5) \approx 10000 \times 0.0111 = 111$ ；
与 20℃的相关性： $k(25,20) = 10000 \times \exp\left(-\frac{(25-20)^2}{50}\right) = 10000 \times \exp\left(-\frac{25}{50}\right) = 10000 \times \exp(-0.5) \approx 10000 \times 0.6065 = 6065$ ；
与 30℃的相关性： $k(25,30) = 10000 \times \exp\left(-\frac{(25-30)^2}{50}\right) = 10000 \times \exp(-0.5) \approx 6065$ ；

所以， $K(x₁^*, X) = [111, 6065, 6065]$ —— 很明显，25℃与相邻的 20℃、30℃相关性极高（6065），与远处的 10℃相关性极低（111），这符合 “近点更相似” 的直觉。

（2）远训练点：x₂*=0℃

同样计算 0℃与训练点的相关性：

与 10℃的相关性： $k(0,10) = 10000 \times \exp\left(-\frac{(0-10)^2}{50}\right) = 10000 \times \exp\left(-\frac{100}{50}\right) = 10000 \times \exp(-2) \approx 10000 \times 0.1353 = 1353$ ；
与 20℃的相关性： $k(0,20) = 10000 \times \exp\left(-\frac{(0-20)^2}{50}\right) = 10000 \times \exp(-8) \approx 10000 \times 0.0003 = 3$ ；
与 30℃的相关性： $k(0,30) = 10000 \times \exp\left(-\frac{(0-30)^2}{50}\right) = 10000 \times \exp(-18) \approx 10000 \times 1.5e-8 = 0.00015$ ；

所以，K(x₂^*, X) = [1353, 3, 0.00015]——0℃只与最近的 10℃有微弱相关性（1353），与 20℃、30℃几乎无关联，这也符合常识：“0℃和 30℃的冰淇淋销量几乎没关系”。

第二步：计算预测均值（μ*）——“最可能的销量”

预测均值的核心逻辑是 “用新点与训练点的相关性，给训练销量做加权平均”。虽然实际计算需要求协方差矩阵的逆 $(K(X,X) + \sigma_n^2 I)^{-1}$ ，但咱们可以简化理解：相关性越高的训练点，权重越大。

（1）近训练点 x₁*=25℃的预测均值

由于 25℃与 20℃、30℃相关性极高（权重占比超 99%），与 10℃相关性极低（权重可忽略），相当于 “主要参考 20℃的 300 和 30℃的 500”：

简化加权计算： $\mu_1^* \approx \frac{6065 \times 300 + 6065 \times 500}{6065 + 6065} = \frac{300 + 500}{2} = 400$ ；
实际考虑 10℃的微弱影响后，最终均值会在 400 左右（比如 398 或 402），波动很小。

这和我们的直觉完全一致：“25℃在 20℃和 30℃之间，销量应该在 300-500 的中间，大概 400”。

（2）远训练点 x₂*=0℃的预测均值

0℃只与 10℃有微弱相关性（1353），与其他训练点几乎无关，所以权重主要集中在 10℃的 100：

简化加权计算： $\mu_2^* \approx \frac{1353 \times 100 + 3 \times 300 + 0.00015 \times 500}{1353 + 3 + 0.00015} \approx \frac{135300 + 900}{1356} \approx 101$ ；

这个结果的含义是：“0℃没有直接数据，只能参考最近的 10℃销量，预测大概 101，但这个值很不确定”——GPR 不会像线性回归那样强行外推一个离谱值（比如线性回归可能算 0℃销量 =-100），而是基于 “最近似的参考” 给出一个合理范围的均值。

第三步：计算预测方差（σ_*^2）——“这个预测有多靠谱”

预测方差是 GPR 的 “王牌”，公式是： $\sigma_*^2 = k(x^*, x^*) - K(x^*, X) \left( K(X,X) + \sigma_n^2 I \right)^{-1} K(X, x^*) + \sigma_n^2$ 。咱们不用硬算矩阵逆，重点看 “相关性对 variance 的影响”：

关键前提：k (x, x) 是固定值

对任意 x*， $k(x^*, x^*) = \sigma_f^2 = 10000$ （因为 x * 和自己的距离为 0，RBF 核中指数部分为 1），所以方差的核心变化来自 “ $K(x^*, X) \times Weight Matrix \times K(X, x^*)$ ” 这一项 —— 我们称之为 “数据带来的方差 reduction（减少量）”。

（1）近训练点 x₁*=25℃的方差

由于K(x₁^*, X) = [111, 6065, 6065]，与训练点相关性高，“数据带来的方差减少量” 很大：

简化理解： $K(x^*, X) \times Weight Matrix \times K(X, x^*) \approx 9900$ （因为相关性高，权重矩阵会放大这种关联，减少不确定性）；
所以， $\sigma_1^{2} \approx 10000 - 9900 + 25 = 125$ ，标准差 $\sigma_1 \approx \sqrt{125} \approx 11$ ；

这意味着：“25℃的销量预测值是 400，不确定性范围是 400±11（95% 置信区间是 400±22），即 378-422”—— 这个范围很窄，说明预测很靠谱，因为离训练数据近。

（2）远训练点 x₂*=0℃的方差

由于K(x₂^*, X) = [1353, 3, 0.00015]，与训练点相关性低，“数据带来的方差减少量” 很小：

简化理解： $K(x^*, X) \times Weight Matrix \times K(X, x^*) \approx 1000$ （相关性低，数据对不确定性的减少作用弱）；
所以， $\sigma_2^{2} \approx 10000 - 1000 + 25 = 9025$ ，标准差 $\sigma_2 \approx \sqrt{9025} = 95$ ；

这意味着：“0℃的销量预测值是 101，不确定性范围是 101±95（95% 置信区间是 101±190），即 - 89-291”—— 这个范围极宽，甚至包含负数，GPR 用这种方式明确告诉你：“0℃没有足够数据支撑，预测结果别当真”。

预测结果的直观对比：近点 “准且确定”，远点 “模糊且谨慎”

把两个预测点的结果放一起，就能清晰看到 GPR 的优势：

预测点 x*	预测均值 μ*（销量）	预测标准差 σ*（不确定性）	95% 置信区间（销量范围）	结论
25℃（近）	400	11	378-422	预测准，不确定性小，可参考
0℃（远）	101	95	-89-291	预测模糊，不确定性大，谨慎参考

这完全符合我们的认知习惯：有数据支撑的地方，结论就靠谱；没数据的地方，就不拍胸脯保证—— 这也是为什么 GPR 在科学实验、工程预测等 “需要严谨性” 的场景里，比普通回归更受欢迎。

再聊一个关键细节：核函数的选择，决定 “函数的先验性格”

前面我们一直用 RBF 核（光滑函数假设），但如果换个核函数，GPR 的先验和结果会完全不同 —— 这就像 “不同的人有不同的初始偏见”，比如有人觉得 “销量应该是光滑的”，有人觉得 “销量有周期性（比如周末高、工作日低）”。

举两个常见的核函数对比：

1. RBF 核（高斯核）：假设函数 “光滑连续”

适合场景：数据没有明显周期性，函数变化平缓（比如温度 - 销量、身高 - 体重）；
特点：函数曲线不会突然跳变，相邻点的预测值相关性高；
例子：用 RBF 核预测冰淇淋销量，会得到一条从 10℃（100）到 30℃（500）的光滑上升曲线。

2. 周期性核（Periodic Kernel）：假设函数 “有重复规律”

公式： $k_{\text{Periodic}}(x, x') = \sigma_f^2 \exp\left(-\frac{2\sin^2\left(\frac{\pi |x - x'|}{T}\right)}{l^2}\right)$ ，其中 T 是周期（比如 7 天，对应 “周周期”）；
适合场景：数据有周期性（比如日期 - 销量、时间 - 用电量）；
特点：函数会随 x 的变化重复某个规律，比如 “每周六销量高，周一销量低”；
例子：如果冰淇淋销量有 “周周期”（周末高 20%），用周期性核做先验，GPR 会在预测周末销量时，自动加入 “周期性溢价”，比 RBF 核更贴合实际。

这说明：核函数是 GPR 的 “灵魂”，它决定了 “你对函数形状的初始假设”—— 选对核函数，GPR 的效果会事半功倍；选不对，就像 “用错了地图，再精准的导航也会偏航”。实际使用时，通常会根据数据的物理意义（比如是否有周期、是否光滑）选择核函数，或者用 “核函数组合”（比如 RBF + 周期性核）应对复杂场景。

总结：GPR 的核心逻辑，其实是 “严谨的贝叶斯思维”

咱们回头看 GPR 的整个流程，其实就是 “贝叶斯公式” 在回归问题上的完美落地：

先验：用高斯过程（均值 + 核函数）描述 “函数可能的形状”，这是 “没有数据时的初始猜测”；
似然：用训练数据和噪声模型（y = f (X) + ε）描述 “数据与函数的关系”，这是 “现实给出的证据”；
后验：通过高斯分布的条件概率，将先验和数据结合，得到 “修正后的函数分布”，这是 “基于证据更新后的结论”；
预测：基于后验分布，给出新点的 “均值（最优预测）+ 方差（不确定性）”，这是 “结论的具体应用”。

很多同学觉得 GPR 难，是因为被 “高斯过程”“协方差矩阵” 这些术语吓住了，但其实剥开数学外衣，它的逻辑特别朴素：用数据修正初始假设，并用不确定性量化 “结论的靠谱程度”。

就像你做实验：先假设 “温度越高，销量越高”（先验），然后测几个温度的销量（数据），再修正为 “温度每高 10℃，销量高 200”（后验），最后预测 25℃销量时，不仅说 “大概 400”，还补充 “误差 ±20”—— 这就是 GPR 的本质，只不过用数学公式把这个过程变得更严谨、可计算了。

所以，不用一开始就死磕矩阵求逆、条件分布推导，先记住 “先验→数据修正→后验→不确定性预测” 这个流程，多看几个可视化案例（比如网上搜 “GPR 先验后验动态图”，能看到函数范围随数据增加而缩小的过程），等直观感觉建立了，再回头啃公式，你会发现：那些复杂的数学，不过是 “把朴素的逻辑翻译成严谨的语言” 而已。

查看全文

http://www.xdnf.cn/news/1420507.html