当前位置：首页 > news >正文

子串：滑动窗口最大值

news 2025/9/2 7:34:49

题目描述：给定一个整数数组和一个固定长度为k的滑动窗口，滑动窗口从数组的左端移到右端，求每个窗口的最大值。

示例

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       31 [3  -1  -3] 5  3  6  7       31  3 [-1  -3  5] 3  6  7       51  3  -1 [-3  5  3] 6  7       51  3  -1  -3 [5  3  6] 7       61  3  -1  -3  5 [3  6  7]      7

求解思路1：单调队列

设滑动窗口索引为[j.......i]，窗口内的最大值为x

则滑动窗口向右移动一位时，窗口索引变为[j+1......i+1]，窗口减去一个数nums[j]，加入一个数nums[i+1]，要算[j+1........i+1]窗口的最大值y，会出现两种情况：

x还在区间内，那么y=max(nums[i+1],x)
x是nums[j]，被移出去了。那么y就得和[j+1......i+1]区间的数重新比较了

根据以上，我们可以维护一个单调非严格递减队列（双端队列且满足队列的数是递增或递减的）

滑动窗口每加入一个新的数，只要新数比已经在窗口的数都大，那么可以把比新数小的数永久删除。队列的第一个元素就是我们的解。

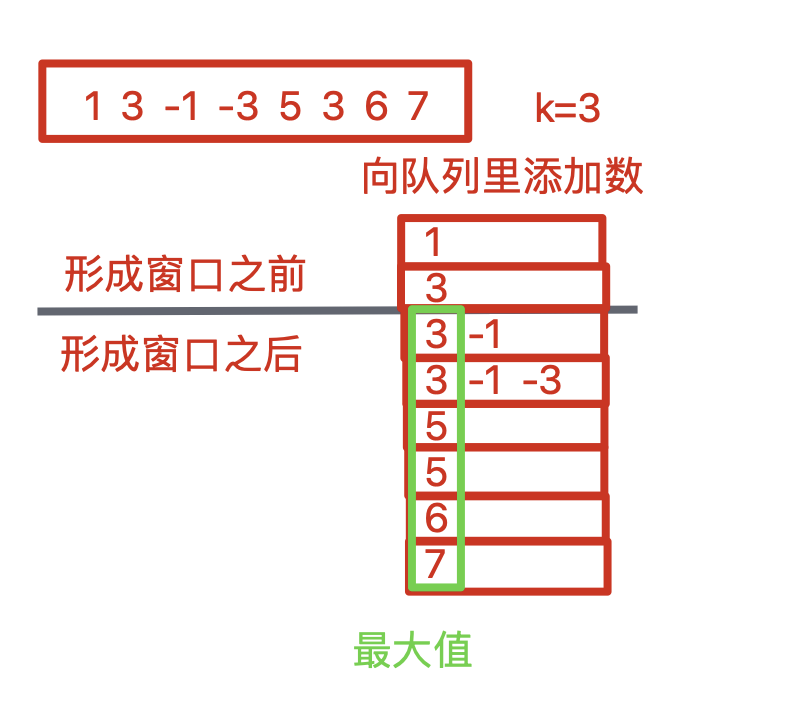
1、形成窗口和未形成窗口分开写

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {// 方法一：单调队列+形成队列和未形成队列分开写int len = nums.length;// 异常判断if (len == 0 || k == 0 || k > len) {return new int[0];}int[] res = new int[len - k + 1];Deque<Integer> queue = new ArrayDeque<>();// 未形成窗口时：窗口区间是[0.....k-1]for (int i = 0; i < k; i++) {while (!queue.isEmpty() && queue.getLast() < nums[i]) {queue.removeLast();}queue.addLast(nums[i]);}res[0] = queue.getFirst(); // 记录第一个窗口的最大值// 形成窗口时：窗口区间是从[1.....k]开始,转成用i表示为[i-k+1.....i]for (int i = k; i < len; i++) {// nums[i-k]可能会在窗口里，移除nums[i-k]if (nums[i - k] == queue.getFirst()) {queue.removeFirst();}while (!queue.isEmpty() && queue.getLast() < nums[i]) {queue.removeLast();}queue.addLast(nums[i]);res[i - k + 1] = queue.getFirst();}return res;}
}

2、形成窗口和未形成窗口合并写

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {// 方法二：单调队列+形成队列和未形成队列合并写int len = nums.length;// 异常判断if (len == 0 || k == 0 || k > len) {return new int[0];}int[] res = new int[len - k + 1];Deque<Integer> queue = new ArrayDeque<>();//窗口[j...i],[i-k+1,0]for (int i = 0, j = 1- k; i < len; j++, i++) {// nums[j-1]可能会在窗口里，移除nums[j-1]if (j > 0 && nums[j-1] == queue.getFirst()) {queue.removeFirst();}while (!queue.isEmpty() && queue.getLast() < nums[i]) {queue.removeLast();}queue.addLast(nums[i]);if (j >= 0) {res[j] = queue.getFirst();}}return res;}
}

求解思路2：大根堆

使用大根堆，nums[j...i]向前滑动nums[j+1,i+1]，窗口每加入元素nums[i]时，确保当前堆中没有nums[j+1]，然后大根堆的堆顶元素就是我们求的解。

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int n = nums.length;// 1. 优先队列存放的是二元组(num,index) : 大顶堆（元素大小不同按元素大小排列，元素大小相同按下标进行排列）// num :   是为了比较元素大小// index : 是为了判断窗口的大小是否超出范围PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>(){public int compare(int[] pair1,int[] pair2){return pair1[0] != pair2[0] ? pair2[0] - pair1[0]:pair2[1] - pair1[1];}});// 2. 优选队列初始化 : k个元素的堆for(int i = 0;i < k;i++){pq.offer(new int[]{nums[i],i});}// 3. 处理堆逻辑int[] res = new int[n - k + 1];         // 初始化结果数组长度 ：一共有 n - k + 1个窗口res[0] = pq.peek()[0];                  // 初始化res[0] ： 拿出目前堆顶的元素for(int i = k;i < n;i++){               // 向右移动滑动窗口pq.offer(new int[]{nums[i],i});     // 加入大顶堆中while(pq.peek()[1] <= i - k){       // 将下标不在滑动窗口中的元素都干掉pq.poll();                      // 维护：堆的大小就是滑动窗口的大小}   res[i - k + 1] = pq.peek()[0];      // 此时堆顶元素就是滑动窗口的最大值}return res;}
}