当前位置：首页 > news >正文

DAY02：【DL 第一弹】pytorch

news 2025/9/2 7:03:16

一、pytorch的概述

1.1 发展历程

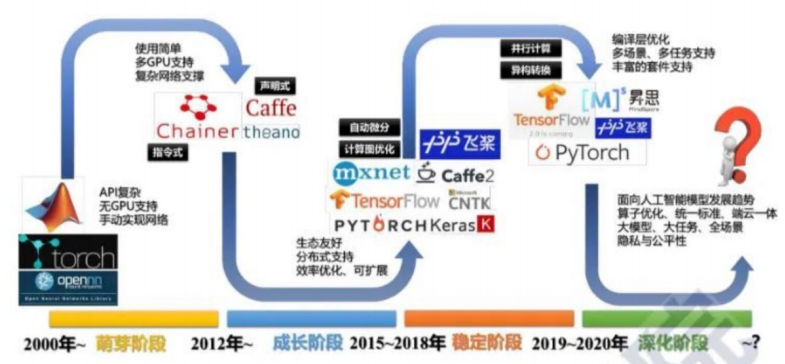
在这里插入图片描述
PyTorch的诞生并非偶然，而是深度学习框架发展到特定阶段的必然产物，其背后是技术需求与生态演变的共同推动。

早在上世纪末，深度学习领域就已出现早期框架，但受限于硬件算力和算法理论，未能广泛普及；
2010年后，随着GPU算力的爆发和大数据时代的到来，深度学习进入高速发展期，此时以Torch为代表的框架开始崭露头角——Torch是一个基于Lua语言的开源深度学习框架，凭借灵活的接口和高效的计算能力，在研究界积累了一定用户，但Lua语言在工业界和科研圈的普及度远不及Python，这一局限性逐渐成为Torch进一步发展的瓶颈；
2016年，Facebook（现Meta）人工智能研究院（FAIR）正式发布PyTorch，其核心目标是解决Torch的语言壁垒：PyTorch基于Python语言开发，完美继承了Python的简洁性和易读性，同时保留了Torch的动态计算图特性。这一设计在当时极具创新性——彼时主流框架（如TensorFlow 1.x）采用静态计算图，需要先定义完整计算流程再运行，调试和迭代效率较低；而PyTorch的动态计算图支持边定义边运行，开发者可以像写普通Python代码一样实时修改计算逻辑，极大降低了科研实验的门槛；
2018年，PyTorch推出1.0版本，这是其发展史上的里程碑。该版本首次融合了动态计算图和静态计算图的优势：动态图适合快速原型开发和调试，静态图则支持模型优化、序列化和部署，满足了从科研到生产的全流程需求。此后，PyTorch的生态开始爆发式增长；
2019年与云服务商（如AWS、Google Cloud）深度合作，推出云端部署工具；
2020年支持移动端部署（PyTorch Mobile），实现训练 - 部署一体化；
2022年发布PyTorch 2.0，引入编译优化，大幅提升计算效率。

如今，PyTorch已成为深度学习领域的双巨头之一（另为TensorFlow）。在学术研究中，超过80%的顶会论文采用PyTorch实现模型；在工业界，微软、特斯拉、NVIDIA 等企业广泛使用其开发计算机视觉、自然语言处理等应用。其成功的核心原因在于：以开发者体验为中心的设计理念、灵活的动态计算模式、完善的生态工具链（如 TorchVision、TorchText、Hugging Face Transformers等），以及活跃的社区支持——全球数百万开发者贡献代码、分享模型，形成了开发 - 反馈 - 迭代的良性循环。

1.2 基本定义

PyTorch是一个以Python为核心的开源深度学习框架，它的本质是一套用于高效处理多维数据、构建和训练神经网络的工具集。与传统编程框架不同，PyTorch专为深度学习场景设计，核心优势在于高效的数值计算与自动求导机制的结合，让开发者能专注于算法逻辑而非底层实现。

1.2.1 数据处理方面

PyTorch的核心是张量（Tensor）——可以简单理解为支持GPU加速的多维数组。在数学上，张量是向量和矩阵的推广：0维张量是标量（如单个数字5），1维张量是向量（如[1,2,3]），2 维张量是矩阵（如[[1,2],[3,4]]），更高维的张量则用于表示复杂数据（如3维张量可表示灰度图像的高度 × 宽度 × 通道，4维张量可表示视频的帧数 × 高度 × 宽度 × 通道）。

与NumPy的数组相比，PyTorch张量有三个关键特性：

跨设备计算：张量可无缝在CPU和GPU之间迁移。例如，通过device='cuda'参数，可将张量存储到GPU中，借助GPU的并行计算能力，将大规模矩阵运算速度提升数十倍——这是深度学习训练的核心需求。
自动求导追踪：通过requires_grad=True参数，张量会自动记录自身参与的所有运算，形成计算图。在神经网络训练时，框架可基于这个计算图，用反向传播算法自动求出参数的梯度，无需手动推导公式——这也是PyTorch简化深度学习开发的核心设计。
面向对象的封装：张量在PyTorch中以类torch.Tensor的形式存在，类中封装了数百种常用运算方法。开发者可以通过张量.方法名()的形式直接调用，无需关注底层实现。

1.2.2 功能定位方面

PyTorch不仅是一个张量计算库，更是一个端到端的深度学习平台。它提供了从数据加载torch.utils.data、模型构建torch.nn、优化器torch.optim到模型保存与加载torch.save/torch.load的全流程工具。例如，用torch.nn.Linear可快速定义一个线性层，用torch.optim.Adam可直接调用Adam优化器，这些封装好的组件让开发者能在几行代码内搭建出复杂的神经网络。

简而言之，PyTorch的核心价值在于：用Python的简洁语法包裹了高效的底层计算（C++/CUDA实现），让开发者既能享受像写普通Python代码一样的开发体验，又能获得接近底层优化的计算性能。无论是科研人员快速验证新算法，还是工程师部署生产级模型，PyTorch都能提供灵活且高效的支持，这也是它能在短短几年内成为主流框架的根本原因。

二、张量的创建

张量作为PyTorch中数据处理的核心载体，其创建方式直接影响后续的计算效率和准确性。根据不同的使用场景（如数据来源、形状要求、数据类型等），PyTorch提供了多种创建张量的方法，每种方法都有其独特的参数和适用场景。

2.1 `torch.tensor` 创建指定数据的张量

torch.tensor是最基础、最常用的张量创建函数，它的核心功能是根据输入数据生成一个新张量，并允许灵活配置张量的属性。无论是单个数值（标量）、Python列表、NumPy数组，还是其他张量，都可以作为输入数据，函数会自动根据输入数据的形状和类型生成对应的张量。

2.1.1 函数定义

torch.tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False, memory_format=torch.contiguous_format)

功能：根据输入数据创建一个新的张量，支持自定义数据类型、设备位置和梯度追踪等属性。
参数说明：
- data：输入数据，用于初始化张量的值和形状。支持多种类型：Python列表、元组、标量、NumPy数组、其他torch.Tensor对象或任意可迭代对象；
- dtype：指定张量的数据类型。若未指定，则自动推断。常见类型：torch.float32（默认）、torch.float64、torch.int32、torch.int64、torch.bool等；
- device：指定张量的存储设备。若未指定，则使用默认设备，通常是CPU。可选值：'cpu'、'cuda'、'cuda:0'等；
- requires_grad：若为True，则该张量将被追踪其计算历史，用于自动求导，适用于训练场景；若为False（默认），则不追踪梯度，适用于推理或中间变量。
返回值：torch.Tensor，一个根据输入参数创建的新张量，包含指定的数据、类型、设备及梯度配置。

✅建议：若需从已有张量创建副本并保留其属性，建议使用tensor.clone()或torch.empty_like()等专用方法以提升效率。

2.1.2 代码示例

# 1.1 创建一个标量张量
data1 = torch.tensor(10)
print(f"data1：{data1}")
# 1.2 创建一个数组张量
data2 = np.random.randn(2, 3)
print(f"data2：{data2}")
data2_ = torch.tensor(data2)
print(f"data2_：{data2_}")
# 1.3 创建一个矩阵张量
data3 = [[10., 20., 30.], [40., 50., 60.]]
print(f"data3：{data3}")
data3_ = torch.tensor(data3)
print(f"data3_：{data3_}")

代码输出：

data1：10
data2：[[-0.8220779   0.89659506  1.37258406][-0.91871932 -0.50791296 -1.13837445]]
data2_：tensor([[-0.8221,  0.8966,  1.3726],[-0.9187, -0.5079, -1.1384]], dtype=torch.float64)
data3：[[10.0, 20.0, 30.0], [40.0, 50.0, 60.0]]
data3_：tensor([[10., 20., 30.],[40., 50., 60.]])

代码解析：

输入为单个标量10，创建的data1是一个0维张量，输出为tensor(10)。标量张量可用于表示单个数值（如损失值）。
先通过np.random.randn生成一个2行3列的NumPy数组（浮点数），再用torch.tensor将其转换为张量。输出中data2_的形状与data2一致，且数据类型自动推断为torch.float64（与NumPy的float64对应）。注意，torch.tensor会复制NumPy数组的数据，两者不共享内存，后续修改互不影响。
输入为嵌套列表（2行3列），torch.tensor直接将其转换为对应形状的张量。由于列表元素是浮点数，张量数据类型默认为torch.float32，输出为2×3的浮点张量。

2.2 `torch.Tensor` 创建指定数据/形状的张量

torch.Tensor是PyTorch中张量的类构造函数，与torch.tensor相比，它的用法和特性有一定差异，尤其在未指定数据时的行为上。

2.2.1 函数定义

torch.Tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False)

功能：创建一个torch.Tensor实例，表示一个多维数组，并支持后续进行各种张量操作，如数学运算、自动求导、GPU加速等。
参数说明：
- data：初始化张量的数据源。支持：Python列表、元组、标量、NumPy数组、其他torch.Tensor对象或任意可迭代结构。数据的形状由输入结构决定；
- dtype：指定张量的数据类型。默认为None，此时根据data自动推断；
- device：指定张量所在的设备。若未指定，则使用当前默认设备，通常为CPU；
- requires_grad：若为True，则启用梯度追踪，该张量参与的运算将被记录，用于反向传播；常用于模型参数训练。默认False，适用于推理或无需梯度的场景；
返回值：一个torch.Tensor类的实例，即一个多维张量对象，其数据、形状、数据类型、设备位置及梯度配置由输入参数决定。

2.2.2 代码示例

data4 = torch.Tensor(2, 3)
print(f"data4：{data4}")
data5 = torch.Tensor([10])
print(f"data5：{data5}")
data6 = torch.Tensor([10, 20])
print(f"data6：{data6}")

代码输出：

data4：tensor([[-4.9975e-04,  1.4013e-42,  0.0000e+00],[ 0.0000e+00,  0.0000e+00,  0.0000e+00]])
data5：tensor([10.])
data6：tensor([10., 20.])

代码解析：

输入为形状(2,3)，torch.Tensor创建一个2行3列的未初始化张量。输出中的数值是内存中的随机值（因未初始化），这一点与torch.tensor不同（torch.tensor必须输入具体数据）。未初始化张量适合需要后续填充数据的场景，可节省初始化时间。
输入为具体数据（列表）时，torch.Tensor会自动推断数据类型为浮点数（即使输入是整数）。因此data5输出为tensor([10.])，data6输出为tensor([10., 20.])，形状分别为(1,)和(2,)。

2.3 `torch.IntTensor`/`torch.FloatTensor`/`torch.DoubleTensor` 创建指定类型的张量

PyTorch提供了一系列以数据类型命名的张量构造函数，如torch.IntTensor（32位整数）、torch.FloatTensor（32位浮点数）、torch.DoubleTensor（64位浮点数）等，它们的核心作用是强制创建特定数据类型的张量，无需手动指定dtype参数，简化了类型控制。

2.3.1 函数定义

（1）`torch.IntTensor`

torch.IntTensor(data=None, device=None, requires_grad=False, pin_memory=False)

功能：创建一个32位有符号整数类型的多维张量。支持从多种数据源初始化，可指定设备位置和梯度追踪。常用于需要整型数据的场景，如索引、类别标签等。
参数说明：
- data：初始化张量的数据，支持列表、元组、NumPy数组、标量或其他张量。若为None，则创建未初始化的张量；
- device：指定张量存储设备，默认为当前默认设备；
- requires_grad：若为True，则记录该张量上的操作用于自动求导，默认为False。
返回值：一个torch.IntTensor类型的张量实例，其数据类型为torch.int32。

（2）`torch.FloatTensor`

torch.FloatTensor(data=None, device=None, requires_grad=False, pin_memory=False)

功能：创建一个32位单精度浮点类型的多维张量。适用于大多数深度学习计算场景，兼顾精度与计算效率，是神经网络中权重和输入数据的常用类型。
参数说明：
- data：输入数据，支持Python列表、NumPy数组、标量等；
- device：目标设备（CPU/GPU），默认为当前默认设备；
- requires_grad：是否启用梯度追踪，默认为False。
返回值：一个torch.FloatTensor类型的张量实例，其数据类型为torch.float32。

（3）`torch.DoubleTensor`

torch.DoubleTensor(data=None, device=None, requires_grad=False, pin_memory=False)

功能：创建一个64位双精度浮点类型的多维张量。提供更高的数值精度，适用于对精度要求较高的科学计算或数值敏感任务。
参数说明：
- data：初始化数据，支持多种数据结构；
- device：张量所在设备，可指定为CPU或CUDA设备；
- requires_grad：是否追踪梯度，默认为False。
返回值：一个torch.DoubleTensor类型的张量实例，其数据类型为torch.float64。

2.3.2 代码示例

data7 = torch.IntTensor(2, 3)
print(f"data7：{data7}")data8 = torch.IntTensor([2.5, 3.7])
print(f"data8：{data8}")
data8_S = torch.ShortTensor([2.5, 3.7])
print(f"data8_S：{data8_S}")
data8_L = torch.LongTensor([2.5, 3.7])
print(f"data8_L：{data8_L}")
data8_F = torch.FloatTensor([2.5, 3.7])
print(f"data8_F：{data8_F}")
data8_D = torch.DoubleTensor([2.5, 3.7])
print(f"data8_D：{data8_D}")

代码输出：

data7：tensor([[-1174207840,        1000,           0],[          0,           0,           0]], dtype=torch.int32)
data8：tensor([2, 3], dtype=torch.int32)
data8_S：tensor([2, 3], dtype=torch.int16)
data8_L：tensor([2, 3])
data8_F：tensor([2.5000, 3.7000])
data8_D：tensor([2.5000, 3.7000], dtype=torch.float64)

代码解析：

torch.IntTensor创建2行3列的32位整数张量，因未输入具体数据，内容为内存随机值（整数），输出中dtype=torch.int32明确了数据类型。
整数类型张量（IntTensor/ShortTensor/LongTensor）接收浮点数输入时，会自动截断小数部分，取整数部分。因此[2.5, 3.7]转换后均为[2, 3]，但数据类型不同，分别为32位、16位、64位整数。
浮点类型张量（FloatTensor/DoubleTensor）会保留输入的小数部分，data8_F为32位浮点数（默认），data8_D为64位浮点数，精度更高，输出中dtype=torch.float64。

2.4 `torch.arange` 创建有序间隔的1维张量

torch.arange用于创建包含半开区间[start, end)内均匀间隔数值的1维张量，类似于Python中的range函数，但返回的是张量而非迭代器。它的核心优势是能快速生成等差数列，适用于需要有序序列的场景，如生成时间步、索引序列等。

2.4.1 函数定义

torch.arange(start=0, end, step=1, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：生成一个1维张量，其元素为在半开区间[start, end)内以固定步长step均匀分布的数值序列。常用于创建索引、坐标轴或数值序列，适用于训练调度、数据采样等场景。
参数：
- start：序列的起始值（包含），默认为0；
- end：序列的结束值（不包含）；
- step：相邻元素之间的步长，默认为1。可为正数（递增）或负数（递减），但不能为零；
- dtype：输出张量的数据类型。若未指定，则根据输入参数自动推断；
- layout：张量的内存布局，默认为torch.strided（密集张量）；
- device：张量存储设备，如'cpu'、'cuda'或'cuda:0'；
- requires_grad：若为True，则启用梯度追踪，用于自动求导，默认为False。
返回值：一个torch.Tensor实例，包含按规则生成的数值，数据类型和设备由参数决定。

2.4.2 代码示例

data9 = torch.arange(0, 10, 2)
print(f"data9：{data9}")

代码输出：

data9：tensor([0, 2, 4, 6, 8])

代码解析：

参数start=0（起始值，包含）、end=10（结束值，不包含）、step=2（步长），因此生成的序列为0，2，4，6，8，输出为1维张量tensor([0, 2, 4, 6, 8])。若省略start，默认从0开始；若step为负数，可生成递减序列。

2.5 `torch.linspace` 创建等距分布的1维张量

torch.linspace用于创建在闭区间[start, end]内均匀分布的steps个元素的1维张量，与torch.arange的核心区别是：arange通过步长控制间隔，而linspace通过元素数量控制间隔，确保首尾元素严格为start和end。

2.5.1 函数定义

torch.linspace(start, end, steps=100, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)

功能：在闭区间[start, end]上生成一个包含steps个元素的一维张量，元素值均匀线性分布。与torch.arange不同，linspace保证始终包含start和end，且元素数量精确可控，适用于需要固定点数的数值采样、坐标轴构建、学习率调度等场景。
参数：
- start：序列的起始值（包含在区间内）；
- end：序列的结束值（包含在区间内）；
- steps：生成的元素个数，默认为100，必须为非负整数。若steps=0，返回空张量；若steps=1，仅返回[start]；否则，在[start, end]区间内等距生成steps个值；
- dtype：输出张量的数据类型。若未指定，则根据start和end自动推断，默认为浮点类型；
- device：张量存储设备，如'cpu'、'cuda'或'cuda:0'；
- requires_grad：若为True，则启用梯度追踪，用于自动求导，默认为False。
返回值：一个torch.Tensor实例，形状为(steps,)，包含在[start, end]区间内均匀分布的steps个数值，其数据类型和设备由参数决定。

2.5.2 代码示例

data10 = torch.linspace(0, 9, 10)
print(f"data10：{data10}")

代码输出：

data10：tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

代码解析：

参数start=0、end=9、steps=10，表示在0到9之间（包含两端）生成10个均匀分布的数。计算间隔为 $(9 - 0) / (10 - 1) = 1$ ，因此序列为0., 1., ..., 9.，输出为浮点型1维张量。若steps=1，则仅返回start；若steps=0，返回空张量。

2.6 `torch.random.init_seed`/`torch.random.manual_seed` 创建随机数

在深度学习中，随机数的可重复性至关重要，torch.random.init_seed和torch.random.manual_seed正是用于控制随机数生成器的种子，确保实验结果可复现。

2.6.1 函数定义

函数	函数签名	功能	参数说明	返回值
`torch.random.init_seed`	`torch.random.init_seed(seed=None)`	初始化随机数生成器的种子。若未提供 `seed`，则自动生成一个随机种子，确保随机性；若提供，则使用该值。影响全局随机状态。	`seed`: 可选整数，用作随机种子；若为`None`，则自动生成	实际使用的种子值（`int` 类型）
`torch.random.manual_seed`	`torch.random.manual_seed(seed)`	手动设置全局随机种子，确保随机操作的可重复性。相同种子下，后续随机序列完全一致。	`seed`: 必需的整数参数，指定随机种子	无（返回 `None`）

2.6.2 代码示例

data10 = torch.randn(2, 3)
print(f"data10：{data10}")
initial_seed = torch.random.initial_seed()
print(f"随机数种子：{initial_seed}")
torch.random.manual_seed(seed=initial_seed)
data11 = torch.randn(2, 3)
print(f"data11：{data11}")

代码输出：

data10：tensor([[-0.3907, -0.3673,  0.0899],[ 1.0603, -0.9746,  0.2568]])
随机数种子：387644933654400
data11：tensor([[-0.3907, -0.3673,  0.0899],[ 1.0603, -0.9746,  0.2568]])

2.7 `torch.ones`/`torch.ones_like` 创建全1张量

2.7.1 函数定义

函数	函数签名	功能	参数说明	返回值
`torch.ones`	`torch.ones(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)`	创建一个指定形状、所有元素为1的张量。	- `*size`：输出形状 - `out`：输出张量 - `dtype`：数据类型 - `layout`：内存布局（默认`strided`） - `device`：设备位置 - `requires_grad`：是否追踪梯度（默认`False`）	一个形状为`size`、元素全为1的`torch.Tensor`，属性由参数决定。
`torch.ones_like`	`torch.ones_like(input, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format)`	创建一个与输入张量形状相同、元素全为1的张量，属性可继承或覆盖。	- `input`：参考张量 - `dtype`：输出类型 - `layout`：内存布局 - `device`：目标设备 - `requires_grad`：是否追踪梯度（默认`False`）	一个与`input`形状相同的全1的`torch.Tensor`，属性由`input`和参数共同决定。

2.7.2 代码示例

data13 = torch.ones(2, 3)
print(f"data13：{data13}")
data13_ = torch.ones_like(data13)
print(f"data13_：{data13_}")

代码输出：

data13：tensor([[1., 1., 1.],[1., 1., 1.]])
data13_：tensor([[1., 1., 1.],[1., 1., 1.]])

代码解析：

data13是2行3列的全1张量（默认浮点型），输出为tensor([[1., 1., 1.], [1., 1., 1.]])。data13_通过ones_like创建，形状与data13一致（2×3），内容同样全为1，避免了手动输入形状的麻烦。

2.8 `torch.zeros`/`torch.zeros_like` 创建全0张量

2.8.1 函数定义

函数	函数签名	功能	参数说明	返回值
`torch.zeros`	`torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)`	创建一个指定形状、所有元素为0的张量，常用于初始化和占位。	- `*size`：输出形状 - `out`：输出张量 - `dtype`：数据类型 - `layout`：内存布局（默认`strided`） - `device`：设备位置 - `requires_grad`：是否追踪梯度（默认`False`）	一个形状为 `size`、元素全为0的`torch.Tensor`，属性由参数决定。
`torch.zeros_like`	`torch.zeros_like(input, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format)`	创建一个与输入张量形状相同、元素全为0的张量，属性可继承或覆盖，适用于结构对齐初始化。	- `input`: 参考张量 - `dtype`: 输出类型 - `layout`：内存布局 - `device`：目标设备 - `requires_grad`：是否追踪梯度（默认`False`） - `memory_format`：内存格式（默认保留输入格式）	一个与`input`形状相同的全0的`torch.Tensor`，属性由`input`和参数共同决定。

2.8.2 代码示例

data12 = torch.zeros(2, 3)
print(f"data12：{data12}")
data12_ = torch.zeros_like(data12)
print(f"data13：{data12_}")

代码输出：

data12：tensor([[0., 0., 0.],[0., 0., 0.]])
data13：tensor([[0., 0., 0.],[0., 0., 0.]])

2.9 `torch.full`/`torch.full_like` 创建指定值填充的张量

2.9.1 函数定义

函数	函数签名	功能	参数说明	返回值
`torch.full`	`torch.full(size, fill_value, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)`	创建一个指定形状、所有元素均为`fill_value`的张量，适用于常数初始化场景。	- `size`：输出形状 - `fill_value`：填充值 - `out`：输出张量 - `dtype`：数据类型 - `device`：设备位置 - `requires_grad`：是否追踪梯度（默认`False`）	一个形状为`size`、元素全为`fill_value`的`torch.Tensor`，属性由参数决定。
`torch.full_like`	`torch.full_like(input, fill_value, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format)`	创建一个与输入张量形状相同、所有元素为`fill_value`的张量，属性可继承或覆盖，适用于结构对齐的常数填充。	- `input`：参考张量 - `fill_value`：填充值 - `dtype`：输出类型 - `layout`：内存布局 - `device`：目标设备 - `requires_grad`：是否追踪梯度（默认`False`） - `memory_format`：内存格式（默认保留输入格式）	一个与`input`形状相同的全`fill_value`张量，属性由`input`和参数共同决定。

2.9.2 代码示例

data14 = torch.full([2, 3], 10)
print(f"data14：{data14}")
data14_ = torch.full_like(data14, 999)
print(f"data14_：{data14_}")

代码输出：

data14：tensor([[10, 10, 10],[10, 10, 10]])
data14_：tensor([[999, 999, 999],[999, 999, 999]])

2.10 `tensor.double`/`tensor.type` 张量类型转换

2.10.1 函数定义

（1）`tensor.double`

tensor.double(memory_format=torch.preserve_format)

功能：将张量的数据类型转换为双精度浮点数类型（torch.float64）。常用于需要更高数值精度的科学计算或调试场景。
参数说明：
- memory_format：指定转换后张量的内存布局，默认为torch.preserve_format。
返回值：一个数据类型为torch.float64的新张量，其值与原张量相同，但精度更高。若原张量已在torch.float64类型下，则返回原张量的视图。

（2）`tensor.type`

tensor.type(dtype=None, tensor=None, memory_format=torch.preserve_format)

功能：通用的类型转换方法，可将张量转换为指定类型。
参数说明：
- dtype：目标数据类型；
- tensor：提供目标类型和设备的参考张量（不推荐）；
- memory_format：内存布局，默认为torch.preserve_format。
返回值：一个类型为torch.float64的新张量。若类型未改变，则可能返回原张量。

2.10.2 代码示例：

data15 = torch.full([2, 3], 100)
print(f"data15的类型：{data15.type()}")
data15_D = data15.type(torch.DoubleTensor)
print(f"data15_D的类型：{data15_D.type()}")
data15_D1 = data15.double()
print(f"data15_D1的类型：{data15_D1.type()}")
data15_S = data15.short()
print(f"data15_S的类型：{data15_S.type()}")
data15_L = data15.long()
print(f"data15_L的类型：{data15_L.type()}")
data15_I = data15.int()
print(f"data15_I的类型：{data15_I.type()}")

代码输出：

data15的类型：torch.LongTensor
data15_D的类型：torch.DoubleTensor
data15_D1的类型：torch.DoubleTensor
data15_S的类型：torch.ShortTensor
data15_L的类型：torch.LongTensor
data15_I的类型：torch.IntTensor

三、张量的类型转换

在PyTorch的实际应用中，张量（Tensor）与其他数据结构的转换是非常常见的操作。这是因为PyTorch擅长深度学习中的张量运算和自动求导，而NumPy则在科学计算、数据预处理等领域更为灵活，两者的协同使用能极大提升开发效率。此外，将张量转换为Python原生标量也常用于结果展示、日志记录等场景。

3.1 `tensor.numpy` 张量→NumPy数组

将PyTorch张量转换为NumPy数组是数据交互的基础操作之一，主要通过张量的numpy()方法实现。但需要特别注意的是，这种转换可能涉及内存共享问题，即转换后的NumPy数组与原张量是否共用同一块内存空间，这直接影响数据修改的关联性。

3.1.1 共享内存的转换

当使用张量的numpy()方法时，生成的NumPy数组会与原张量共享内存。这意味着：如果修改NumPy数组中的元素，原张量的对应元素会同步发生变化；反之，修改原张量的元素，NumPy数组也会受到影响。这种特性的底层原因是，PyTorch张量和NumP数组在CPU上的内存布局兼容，numpy()方法仅构建了新的数组对象，但未复制数据，从而节省了内存和计算资源。

3.1.2 不共享内存的转换

如果希望转换后的NumPy数组与原张量完全独立，即修改互不影响，可以通过np.array()结合copy()方法实现。np.array(tensor)会尝试创建新数组，但默认情况下可能仍共享内存；而copy()方法会强制复制数据，彻底切断两者的内存关联。

3.1.3 代码示例

## 1.1 共享内存
torch.random.manual_seed(42)
data1 = torch.randint(0, 10, [2, 3])
print(f"data1：{data1}")
print(f"data1的类型：{type(data1)}")
data1_numpy = data1.numpy()
print(f"data1_numpy：{data1_numpy}")
print(f"data1_numpy的类型：{type(data1_numpy)}")data1_numpy[0] = 100
print(f"data1_numpy：{data1_numpy}")
print(f"data1：{data1}")
## 1.2 不共享内存
data2 = torch.tensor([2, 3, 4])
data2_numpy = np.array(data2).copy()data2_numpy[0] = 100
print(f"data2_numpy：{data2_numpy}")
print(f"data2：{data2}")

代码输出：

data1：tensor([[2, 7, 6],[4, 6, 5]])
data1的类型：<class 'torch.Tensor'>
data1_numpy：[[2 7 6][4 6 5]]
data1_numpy的类型：<class 'numpy.ndarray'>
data1_numpy：[[100 100 100][  4   6   5]]
data1：tensor([[100, 100, 100],[  4,   6,   5]])
data2_numpy：[100   3   4]
data2：tensor([2, 3, 4])

3.2 `torch.from_numpy` NumPy数组→张量

与张量转NumPy数组相对应，将NumPy数组转换为PyTorch张量同样是高频操作，主要通过torch.from_numpy()和torch.tensor()两种方式实现，两者的核心区别仍在于是否共享内存。

3.2.1 共享内存的转换

torch.from_numpy(numpy_array)是将NumPy数组转换为张量的高效方法，其生成的张量与原NumPy数组共享内存。这意味着：修改张量的元素会同步修改原NumPy数组，反之亦然。这种设计的目的是减少数据复制，提升转换效率，尤其适用于大规模数据的快速转换。

3.2.2 不共享内存的转换

torch.tensor(numpy_array)同样可以将NumPy数组转换为张量，但与from_numpy()不同，它会复制原数组的数据，生成一个全新的张量，两者不共享内存。因此，修改张量不会影响原NumPy数组，反之亦然。

3.2.3 代码示例

## 2.1 torch.from_numpy 共享内存
data3 = np.array([2, 3, 4])
data3_torch = torch.from_numpy(data3)
print(f"data3：{data3}")
print(f"data3_torch：{data3_torch}")data3_torch[0] = 100
print(f"data3_torch：{data3_torch}")
print(f"data3：{data3}")
## 2.2 torch.tensor 不共享内存
data4 = np.array([2, 3, 4])
data4_torch = torch.tensor(data4)data4_torch[0] = 100
print(f"data4_torch：{data4_torch}")
print(f"data4：{data4}")

代码输出：

data3：[2 3 4]
data3_torch：tensor([2, 3, 4], dtype=torch.int32)
data3_torch：tensor([100,   3,   4], dtype=torch.int32)
data3：[100   3   4]
data4_torch：tensor([100,   3,   4], dtype=torch.int32)
data4：[2 3 4]

3.3 `item` 张量→Python标量

在模型训练或推理过程中，我们经常需要将单个元素的张量（如损失值、评价指标）转换为Python原生标量（如int、float），以便进行打印、日志记录或与其他Python库（如matplotlib绘图）交互。item()方法就是实现这一转换的核心工具。

3.3.1 基本条件

item()方法仅适用于单个元素的张量，包括两种情况：

0维张量（标量）：如torch.tensor(5)，直接存储单个数值。
1维单元素张量：如torch.tensor([5,])，形状为(1,)，仅包含一个元素。

对于包含多个元素的张量，如形状为(2,3)的矩阵，调用item()会报错，因为无法确定要提取哪个元素。

3.3.2 代码示例

data5 = torch.tensor(5)
print(f"data5：{data5.item()}")
data5_ = torch.tensor([5, ])
print(f"data5_：{data5_.item()}")

代码输出：

data5：5
data5_：5

四、张量的数值计算

在PyTorch中，张量的数值计算是实现深度学习模型核心逻辑的基础，包括基础四则运算、元素级乘法（点乘）、矩阵乘法等操作。这些运算不仅支持标量与张量、张量与张量之间的交互，还通过就地操作等特性优化内存使用，满足高效计算需求。

4.1 四则运算

张量的四则运算（加、减、乘、除、取负）是最基础的数值操作，PyTorch提供了两类接口：非就地操作（如add()、sub()）和就地操作（如add_()、sub_()），两者的核心区别在于是否修改原张量。

4.1.1 非就地操作

非就地操作会创建新的张量存储运算结果，原张量的值保持不变。以加法为例，tensor.add(other)会返回一个新张量，其值为原张量与other（可以是标量、同形状张量）相加的结果，而原张量本身不会被修改。这种特性保证了原始数据的安全性，适合需要保留中间结果的场景，如模型训练中的多步计算。

函数	函数签名	功能	参数说明	返回值
`add()`	`torch.add(input, other, *, alpha=1, out=None)`	执行逐元素加法：`input + alpha * other`	- `input`：被加数张量 - `other`：加数（张量或标量） - `alpha`：`other`的缩放系数（默认1）	一个新的`Tensor`，包含加法结果。
`sub()`	`torch.sub(input, other, *, alpha=1, out=None)`	执行逐元素减法：`input - alpha * other`	- `input`：被减数 - `other`：减数（张量或标量） - `alpha`：缩放系数	一个新的`Tensor`，值为减法结果。
`mul()`	`torch.mul(input, other, *, out=None)`	执行逐元素乘法：`input * other`，支持广播	- `input`、`other`：乘数（可为张量或标量）	一个新的`Tensor`，包含逐元素乘积。
`div()`	`torch.div(input, other, *, rounding_mode=None, out=None)`	执行逐元素除法：`input / other`，可指定舍入模式	- `input`：被除数 - `other`：除数（≠0） - `rounding_mode`：舍入方式，支持`'trunc'`、`'floor'`等	一个新的`Tensor`，值为除法结果。
`neg()`	`torch.neg(input, *, out=None)`	对张量中每个元素取负：`-input`	- `input`：输入张量	一个新的`Tensor`，值为原张量的负值。

4.1.2 就地操作

就地操作（方法名末尾带下划线）与非就地操作的功能相同，但会直接修改原张量的值，不创建新对象，从而节省内存开销。例如tensor.add_(other)等价于tensor = tensor + other，运算后原张量的值被更新为计算结果。

这种操作在处理大规模张量时优势明显，尤其是在循环迭代或需要频繁更新张量的场景（如梯度下降中的参数更新），可减少内存分配与释放的开销。但需特别注意：就地操作会覆盖原张量的数据，若后续计算仍需原始值，需提前备份，例如tensor_copy = tensor.clone()。

函数	函数签名	功能	参数说明	返回值
`add_()`	`tensor.add_(other, *, alpha=1)`	加法：`tensor = tensor + alpha * other`	- `other`：加数（张量或标量） - `alpha`：缩放系数（默认1）	修改后的原张量（`tensor`）
`sub_()`	`tensor.sub_(other, *, alpha=1)`	减法：`tensor = tensor - alpha * other`	- `other`：减数 - `alpha`：缩放系数	修改后的原张量
`mul_()`	`tensor.mul_(other)`	乘法：`tensor = tensor * other`	- `other`：乘数（张量或标量）	修改后的原张量
`div_()`	`tensor.div_(other, *, rounding_mode=None)`	除法：`tensor = tensor / other`	- `other`：除数（≠0） - `rounding_mode`：舍入模式	修改后的原张量
`neg_()`	`tensor.neg_()`	取负：`tensor = -tensor`	`\`	返回修改后的原张量

4.1.3 代码示例

data1 = torch.randint(0, 10, [2, 3])
print(f"data1：{data1}")
## 1.1 add/add_ 矩阵相加
data1_add = data1.add(10)
print(f"data1_add：{data1_add}")
print(f"data1：{data1}")data1_add_ = data1.add_(100)
print(f"data1_add_：{data1_add_}")
print(f"data1：{data1}")
## 1.2 sub/sub_ 矩阵相减
data1_sub = data1.sub(10)
print(f"data1_sub：{data1_sub}")
## 1.3 mul/mul_ 矩阵相乘
data1_mul = data1.mul(100)
print(f"data1_mul：{data1_mul}")
## 1.4 div/div_ 矩阵相除
data1_div = data1.div(10)
print(f"data1_div：{data1_div}")
## 1.5 neg/neg_ 矩阵取负
data1_neg = data1.neg()
print(f"data1_neg：{data1_neg}")

代码输出：

data1：tensor([[7, 2, 1],[3, 0, 0]])
data1_add：tensor([[17, 12, 11],[13, 10, 10]])
data1：tensor([[7, 2, 1],[3, 0, 0]])
data1_add_：tensor([[107, 102, 101],[103, 100, 100]])
data1：tensor([[107, 102, 101],[103, 100, 100]])
data1_sub：tensor([[97, 92, 91],[93, 90, 90]])
data1_mul：tensor([[10700, 10200, 10100],[10300, 10000, 10000]])
data1_div：tensor([[10.7000, 10.2000, 10.1000],[10.3000, 10.0000, 10.0000]])
data1_neg：tensor([[-107, -102, -101],[-103, -100, -100]])

4.2 点乘运算

点乘（Hadamard 积）是张量元素级的乘法运算，即两个形状相同的张量对应位置的元素相乘，结果张量的形状与输入张量一致。在PyTorch中，点乘可通过torch.mul(tensor1, tensor2)或运算符*实现，其核心是逐元素对应计算。

4.2.1 函数定义

torch.mul(input, other, *, out=None)

功能：实现两个张量或一个张量与一个标量之间的逐元素（element-wise）乘法运算。
参数说明：
- input：被乘数张量，即参与乘法运算的第一个输入；
- other：乘数，可以是一个与input形状兼容的张量，或一个标量数值；
- out：可选的输出张量，用于存储运算结果。如果指定，则其形状必须与广播后的结果一致。
返回值：一个新的张量，其值为input与other逐元素相乘的结果。返回张量的形状由输入的广播规则决定，数据类型通常与输入张量一致或根据类型提升规则确定。

4.2.2 数学定义

点乘的数学定义为：对于两个形状相同的张量 $A$ 和 $B$ ，其点乘结果 $C$ 满足 $Ci,j=Ai,j×Bi,jC_{i,j} = A_{i,j} \times B_{i,j}$ （以二维张量为例）。这要求两个输入张量的形状必须完全一致，否则会触发维度不匹配的错误（如3×4的张量与4×4的张量无法点乘）。

假设：
$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$
则 $A$ ， $B$ 的Hadamard积：
$\circ B = \begin{bmatrix} 1 \times 5 & 2 \times 6 \\ 3 \times 7 & 4 \times 8 \end{bmatrix} = \begin{bmatrix} 5 & 12 \\ 21 & 32 \end{bmatrix}$

4.2.3 应用场景

点乘在深度学习中应用广泛，例如：

特征缩放：用一个掩码张量（元素为0或1）与特征张量点乘，可实现对特定特征的保留或屏蔽。
元素级权重调整：通过点乘为张量的不同元素分配不同权重，如注意力机制中对特征重要性的加权。
逐元素激活函数：某些激活函数的计算可视为输入张量与权重张量的点乘。

与矩阵乘法相比，点乘的计算复杂度更低（ $O (n)$ ， $n$ 为元素总数），且无需考虑维度匹配的严格规则（仅需形状相同），因此更适合简单的元素级数值调整。

4.2.4 代码示例

torch.random.manual_seed(42)
data2 = torch.randint(0, 10, [3, 4])
print(f"data2：{data2}")torch.random.manual_seed(43)
data3 = torch.randint(0, 10, [3, 4])
print(f"data3：{data3}")
print(f"data2*data3：{torch.mul(data2, data3)}")
print(f"data2*data3：{data2*data3}")# 1×. 维度不匹配
# torch.random.manual_seed(44)
# data4 = torch.randint(0, 10, [4, 4])
# print(f"data4：{data4}")
# print(f"data2*data4：{torch.mul(data2, data4)}")
# # RuntimeError: The size of tensor a (3) must match the size of tensor b (4) at non-singleton dimension 0

代码输出：

data2：tensor([[2, 7, 6, 4],[6, 5, 0, 4],[0, 3, 8, 4]])
data3：tensor([[8, 8, 5, 7],[5, 0, 0, 1],[7, 9, 1, 0]])
data2*data3：tensor([[16, 56, 30, 28],[30,  0,  0,  4],[ 0, 27,  8,  0]])
data2*data3：tensor([[16, 56, 30, 28],[30,  0,  0,  4],[ 0, 27,  8,  0]])

代码解析：

data2（3×4）与data3（3×4）点乘后，结果为3×4的张量，每个元素是对应位置的乘积（如第一行第一列：2×8=16）。若尝试用形状不匹配的张量（如3×4与4×4）进行点乘，PyTorch会抛出RuntimeError，提示维度不匹配，这是为了保证元素级运算的一一对应关系。

4.3 矩阵乘法运算

矩阵乘法（也称矩阵积）是线性代数中的核心运算，与点乘的元素级计算不同，它通过行与列的内积实现维度变换，在神经网络中用于实现特征的线性变换（如全连接层的计算）。PyTorch中可通过torch.matmul(tensor1, tensor2)或运算符@实现。

4.3.1 函数定义

torch.matmul(input, other, *, out=None)

功能：执行两个张量之间的矩阵乘法运算，支持向量、矩阵以及高维张量之间的多种乘法模式（如向量点积、矩阵-向量乘法、矩阵-矩阵乘法、批处理矩阵乘法等）。
参数说明：
- input：第一个输入张量，参与矩阵乘法的左操作数；
- other：第二个输入张量，参与矩阵乘法的右操作数；
- out：可选的输出张量，用于存储计算结果。其形状必须与预期输出匹配。
返回值：一个新的张量，表示input和other的矩阵乘法结果。输出张量的形状取决于输入张量的维度和广播规则。

4.3.2 数学定义

矩阵乘法的核心约束是：第一个张量的列数必须等于第二个张量的行数。若张量 $A$ 的形状为 $(m, n)$ ，张量 $B$ 的形状为 $(n, p)$ ，则它们的乘积 $C$ 的形状为 $(m, p)$ ，其中 $Ci,j=∑k=1nAi,k×Bk,jC_{i,j} = \sum_{k=1}^{n} A_{i,k} \times B_{k,j}$ （第 $i$ 行与第 $j$ 列的内积）。

矩阵乘法不仅适用于二维张量，还可扩展到高维张量（如批量矩阵乘法），但核心规则不变：最后两个维度需满足前一列数=后一行数。例如，形状为 $(b, m, n)$ 的批量张量与 $(b, n, p)$ 的批量张量相乘，结果为 $(b, m, p)$ ，其中 $b$ 为批量大小。

在深度学习中，矩阵乘法是构建模型的基础：

全连接层中，输入特征（形状为 $batch, in\_features)$ ）与权重矩阵（形状为 $in\_features, out\_features)$ ）相乘，得到输出特征（ $batch, out\_features)$ ）；
卷积操作的底层实现也依赖矩阵乘法（将卷积核与输入特征展开后计算）。

需注意，矩阵乘法不满足交换律（ $\neq B@A$ ），且计算复杂度较高（ $O (mn p)$ ），因此在处理大规模张量时需关注性能优化。

4.3.3 代码示例

torch.random.manual_seed(42)
data5 = torch.randint(0, 10, [3, 4])
print(f"data5：{data5}")torch.random.manual_seed(43)
data6 = torch.randint(0, 10, [4, 5])
print(f"data6：{data6}")
print(f"data5@data6：{torch.matmul(data5, data6)}")
print(f"data5@data6：{data5@data6}")

代码输出：

data5：tensor([[2, 7, 6, 4],[6, 5, 0, 4],[0, 3, 8, 4]])
data6：tensor([[8, 8, 5, 7, 5],[0, 0, 1, 7, 9],[1, 0, 4, 4, 7],[2, 1, 9, 6, 3]])
data5@data6：tensor([[ 30,  20,  77, 111, 127],[ 56,  52,  71, 101,  87],[ 16,   4,  71,  77,  95]])
data5@data6：tensor([[ 30,  20,  77, 111, 127],[ 56,  52,  71, 101,  87],[ 16,   4,  71,  77,  95]])

五、张量的计算函数

在PyTorch中，张量的计算函数是对张量进行统计分析、数值转换和数学运算的核心工具。这些函数不仅支持对张量整体的计算（如求总和、均值），还能按指定维度进行操作，同时涵盖了平方根、指数、对数等基础数学运算。掌握这些函数的用法，对于数据预处理、特征工程以及模型训练中的损失计算、梯度更新等环节至关重要。

5.1 函数定义

5.1.1 `tensor.sum` 求和

sum(arr, axis=None, dtype=None, keepdims=False)

功能：计算输入数组或序列中所有元素的总和。支持沿指定轴（维度）进行求和，并可控制输出数据类型和维度保留行为。
参数说明：
- arr：输入数组或序列，元素需支持加法运算；
- axis：指定求和操作的轴。默认为None，表示对所有元素求和；
- dtype：指定累加和结果的数据类型。若未指定，则根据输入自动推断；
- keepdims：若为True，则在结果中保留被压缩的维度（长度为1），便于后续广播操作。
返回值：沿指定轴求和的标量（当axis=None时）或数组。若 keepdims=True，输出维度与输入相同，仅被求和轴长度为1。

5.1.2 `tensor.mean` 求均值

mean(arr, axis=None, dtype=None, keepdims=False, skipna=True)

功能：计算输入数组或序列中元素的算术平均值（总和/有效元素个数）。支持沿指定轴求均值，可忽略缺失值（如NaN或None），并保留维度结构。
参数说明：
- arr：输入数组或序列，元素应支持算术运算；
- axis：指定求均值的轴，默认None表示全局均值；
- dtype：指定结果的数据类型，常用于精度控制；
- keepdims：是否保留求均值后的维度结构；
- skipna：是否忽略NaN或缺失值。若为True，仅基于非缺失值计算均值。
返回值：包含输入数据平均值的标量或数组，形状由axis和keepdims决定；若存在缺失值且skipna=True，则自动排除。

5.1.3 `tensor.sqrt` 求平方根

sqrt(x)

功能：计算输入值的平方根（√x），支持标量、数组或序列输入，逐元素操作。
参数说明：
- x：输入值，建议为非负数。负数输入可能导致返回NaN或引发异常，取决于后端实现。
返回值：与输入x形状相同的标量或数组，每个元素为对应输入的平方根值。

5.1.4 `tensor.pow`/`tensor.exp` 求指数

（1）`tensor.pow`

pow(base, exp)

功能：计算底数的指数次幂（即 $base^{exp}$ ），支持标量与数组的广播运算。
参数说明：
- base：幂运算的底数；
- exp：幂运算的指数，需与base可广播。
返回值：与广播后形状一致的数组或标量，每个元素为对应base的exp次幂。

（2）`tensor.exp`

exp(x)

功能：计算自然指数函数 $e^x$ ，其中 $e \approx 2.71828$ ，支持标量或数组输入，逐元素计算。
参数说明：
- x：输入值，可为任意实数。
返回值：与输入同形状的标量或数组，每个元素为 $e^{input}$ 的值。

5.1.5 `tensor.log` 求对数

log(x, base=None)

功能：计算输入值的对数。默认为自然对数（以 $e$ 为底，即 $l n x$ ）；若指定 base，则计算以该值为底的对数。
参数说明：
- x：输入值，必须为正数，否则结果为NaN或报错；
- base：对数的底数。默认None表示自然对数；可设为2、10等常用底数。
返回值：与输入同形状的标量或数组，每个元素为对应输入的对数值（自然对数或指定底数的对数）。

5.2 代码示例

import torchtorch.random.manual_seed(42)
data1 = torch.rand([3, 4])
print(f"data1：{data1}")# 1. mean 求均值
data1_mean = data1.mean()
print(f"data1_mean：{data1_mean}")
print(f"dim=0：{data1.mean(dim=0)}")
print(f"dim=1：{data1.mean(dim=1)}")print('--'*50)
# 2. sum 求和
data1_sum = data1.sum()
print(f"data1_sum：{data1_sum}")
print(f"dim=0：{data1.sum(dim=0)}")
print(f"dim=1：{data1.sum(dim=1)}")print('--'*50)
# 3. sqrt 求平方根
data1_sqrt = data1.sqrt()
print(f"data1_sqrt：{data1_sqrt}")print('--'*50)
# 4. pow 求指数
data1_pow = data1.pow(2)
print(f"data1_pow：{data1_pow}")
data1_exp = data1.exp()
print(f"data1_exp：{data1_exp}")print(f"2**data1：{torch.pow(2, data1)}")
print(f"data1**2：{torch.pow(data1, 2)}")print('--'*50)
# 5. log 求对数
print(f"loge：{data1.log()}")
print(f"log2：{data1.log2()}")
print(f"log10：{data1.log10()}")

代码输出：

data1：tensor([[0.8823, 0.9150, 0.3829, 0.9593],[0.3904, 0.6009, 0.2566, 0.7936],[0.9408, 0.1332, 0.9346, 0.5936]])
data1_mean：0.6485946178436279
dim=0：tensor([0.7378, 0.5497, 0.5247, 0.7822])
dim=1：tensor([0.7849, 0.5104, 0.6505])
----------------------------------------------------------------------------------------------------
data1_sum：7.783135414123535
dim=0：tensor([2.2135, 1.6491, 1.5740, 2.3465])
dim=1：tensor([3.1394, 2.0416, 2.6021])
----------------------------------------------------------------------------------------------------
data1_sqrt：tensor([[0.9393, 0.9566, 0.6188, 0.9794],[0.6249, 0.7752, 0.5065, 0.8909],[0.9699, 0.3649, 0.9667, 0.7704]])
----------------------------------------------------------------------------------------------------
data1_pow：tensor([[0.7784, 0.8372, 0.1466, 0.9203],[0.1524, 0.3611, 0.0658, 0.6299],[0.8851, 0.0177, 0.8735, 0.3523]])
data1_exp：tensor([[2.4164, 2.4968, 1.4665, 2.6099],[1.4776, 1.8238, 1.2925, 2.2114],[2.5620, 1.1425, 2.5462, 1.8105]])
2**data1：tensor([[1.8433, 1.8856, 1.3039, 1.9444],[1.3108, 1.5167, 1.1946, 1.7334],[1.9196, 1.0967, 1.9114, 1.5090]])
data1**2：tensor([[0.7784, 0.8372, 0.1466, 0.9203],[0.1524, 0.3611, 0.0658, 0.6299],[0.8851, 0.0177, 0.8735, 0.3523]])
----------------------------------------------------------------------------------------------------
loge：tensor([[-0.1253, -0.0888, -0.9601, -0.0415],[-0.9405, -0.5093, -1.3603, -0.2311],[-0.0611, -2.0160, -0.0676, -0.5216]])
log2：tensor([[-0.1807, -0.1282, -1.3851, -0.0599],[-1.3568, -0.7348, -1.9626, -0.3334],[-0.0881, -2.9085, -0.0976, -0.7525]])
log10：tensor([[-0.0544, -0.0386, -0.4170, -0.0180],[-0.4084, -0.2212, -0.5908, -0.1004],[-0.0265, -0.8755, -0.0294, -0.2265]])

六、张量的索引操作

张量的索引操作是PyTorch中获取、筛选张量元素的核心手段，类似于NumPy数组的索引逻辑，但针对张量的多维特性做了适配。通过索引，我们可以精准定位张量中的特定元素、子张量或满足条件的元素，是数据预处理、特征提取和模型推理中的基础操作。

6.1 行列索引

行列索引是针对二维张量（矩阵）最基础的索引方式，通过指定行索引和列索引来定位元素，适用于从矩阵中提取单行、单列或单个元素。其核心逻辑是：对于形状为(m, n)的二维张量，第一个索引表示行位置（范围0~m-1），第二个索引表示列位置（范围0~n-1），用逗号分隔；若只指定一个索引，则默认提取整行。

值得注意的是，索引从0开始（即首行/首列为0），且超过范围的索引会报错。这种方式适用于快速提取矩阵中的单行、单列或单个元素，是数据分析中查看局部数据的常用操作。

代码示例：

torch.random.manual_seed(42)
data1 = torch.randint(0, 10, [4, 5])
print(f"data1：{data1}")print(f"data1[0]：{data1[0]}")
print(f"data1[0, 0]：{data1[0, 0]}")
print(f"data1[:, 0]：{data1[:, 0]}")

代码输出：

data1：tensor([[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]])
data1[0]：tensor([2, 7, 6, 4, 6])
data1[0, 0]：2
data1[:, 0]：tensor([2, 5, 8, 2])

代码解析：

data1[0]表示提取第0行（首行）的所有元素。由于只指定了行索引0，因此返回该行的所有列元素，结果为形状(5,)的1维张量：tensor([2, 7, 6, 4, 6])。
data1[0, 0]表示提取第0行第0列的单个元素。这里第一个索引0指定行，第二个索引0指定列，定位到矩阵左上角的元素，结果为标量2。
data1[:, 0]中，冒号:表示所有行，第二个索引0表示第0列，因此返回所有行的第0列元素，结果为形状(4,)的1维张量：tensor([2, 5, 8, 2])。

6.2 列表索引

列表索引允许通过列表形式指定多个行索引和列索引，一次性提取多个不连续的元素或子张量，适用于需要非连续位置数据的场景。其核心规则是：若行索引为列表[i1, i2, ...]，列索引为列表[j1, j2, ...]，则返回的元素为(i1,j1), (i2,j2), ...位置的元素，且两个列表的长度必须相同；若行索引为多维列表（如二维列表），则会与列索引进行广播，生成更高维度的子张量。

列表索引的灵活性在于可以跳过连续范围，直接提取分散的元素。例如，若需要提取第0行第3列、第2行第4列的元素，可直接使用data1[[0,2], [3,4]]，无需循环或多次索引。值得注意的是，行索引和列索引的长度必须兼容（要么长度相同，要么可广播），否则会报维度不匹配错误。

代码示例：

torch.random.manual_seed(42)
data1 = torch.randint(0, 10, [4, 5])print(f"data1[[0, 1], [1, 2]]：{data1[[0, 1], [1, 2]]}")
print(f"data1[[[0], [1]], [1, 2]]：{data1[[[0], [1]], [1, 2]]}")

代码输出：

data1[[0, 1], [1, 2]]：tensor([7, 4])
data1[[[0], [1]], [1, 2]]：tensor([[7, 6],[0, 4]])

代码解析：

data1[[0, 1], [1, 2]]中，行索引为[0, 1]（第0行、第1行），列索引为[1, 2]（第1列、第2列）。根据规则，返回的是(0,1)和(1,2)两个位置的元素。查看data1可知，(0,1)为7，(1,2)为4，因此结果为tensor([7, 4])。
data1[[[0], [1]], [1, 2]]中，行索引为二维列表[[0], [1]]（形状(2,1)），列索引为[1, 2]（形状(2,)）。由于列表形状不同，会触发广播机制：行索引的每个元素[0]和[1]会分别与列索引的[1,2]匹配，即(0,1)、(0,2)和(1,1)、(1,2)。对应元素分别为7、6、0、4，因此结果为形状(2,2)的张量。

6.3 范围索引

范围索引（又称切片索引）通过[start:end:step]的形式指定连续的索引范围，适用于提取张量中某一连续区间的子张量，是批量获取数据的高效方式。其核心规则是：

start：范围起始索引（包含，默认0）；
end：范围结束索引（不包含，默认张量维度长度）；
step：步长（默认1，即连续提取）；

若省略start，表示从0开始；省略end，表示到最后一个元素；省略step，表示步长为1。

范围索引的优势在于高效性：它不需要复制数据，而是返回原张量的视图（共享内存），因此操作速度快且节省内存。例如，对data1[:3, :2]修改元素会影响原张量data1中对应位置的值。这种特性使其在处理大型张量时尤为实用，常用于数据分块、窗口滑动等场景。

代码示例：

torch.random.manual_seed(42)
data1 = torch.randint(0, 10, [4, 5])print(f"data1[:3, :2]：{data1[:3, :2]}")
print(f"data1[2:, 2:]：{data1[2:, 2:]}")

代码输出：

data1[:3, :2]：tensor([[2, 7],[5, 0],[8, 4]])
data1[2:, 2:]：tensor([[0, 4, 1],[5, 7, 6]])

6.4 布尔索引

布尔索引通过布尔张量（元素为True或False）筛选元素，仅保留布尔张量中True位置对应的元素，适用于按条件提取数据（如筛选大于某个阈值的元素）。其核心逻辑是：布尔张量的形状必须与被索引的张量维度兼容（要么形状相同，要么可广播），True表示选中对应位置的元素，False表示排除。

布尔索引的关键是条件表达式的构建，通过比较运算符（>、<、==等）或逻辑运算符（&、|、~等）可组合出复杂条件。例如，(data1 > 5) & (data1 % 2 == 0)可筛选出大于5且为偶数的元素。值得注意的是，布尔索引返回的是原张量的副本（不共享内存），修改结果不会影响原张量，这与范围索引不同。

代码示例：

torch.random.manual_seed(42)
data1 = torch.randint(0, 10, [4, 5])index_1 = data1[:, 2]>5
print(f"index_1：{index_1}")
print(f"data1[index_1]：{data1[index_1]}")index_2 = data1[2]>3
print(f"index_2：{index_2}")
print(f"data1[:, index_2]：{data1[:, index_2]}")

代码输出：

index_1：tensor([ True, False, False, False])
data1[index_1]：tensor([[2, 7, 6, 4, 6]])
index_2：tensor([ True,  True, False,  True, False])
data1[:, index_2]：tensor([[2, 7, 4],[5, 0, 0],[8, 4, 4],[2, 5, 7]])

代码解析：

行筛选：index_1 = data1[:, 2] > 5中，data1[:, 2]表示第2列的所有元素（tensor([6, 4, 0, 5])），条件>5会生成布尔张量tensor([True, False, False, False])（只有第0行的第2列元素6满足条件）。用data1[index_1]筛选行时，仅保留True对应的第0行，结果为tensor([[2, 7, 6, 4, 6]])。
列筛选：index_2 = data1[2] > 3中，data1[2]表示第2行的所有元素（tensor([8, 4, 0, 4, 1])），条件>3生成布尔张量tensor([True, True, False, True, False])（第0、1、3列满足条件）。用data1[:, index_2]筛选列时，保留True对应的列。

6.5 多维索引

多维索引适用于三维及以上的张量（如批量图像数据的(batch, height, width)结构），通过多个逗号分隔的索引分别指定每个维度的位置，从而提取高维子张量。其核心规则是：索引的数量与张量的维度一致，每个索引可以是整数、冒号（表示所有元素）、列表或范围，分别对应不同维度的筛选逻辑。

代码示例：

torch.random.manual_seed(42)
data2 = torch.randint(0, 10, [3, 4, 5])
print(f"data2：{data2}")
print(f"data2[0, 0, 0]：{data2[0, 0, 0]}")
print(f"data2[0, :, 0]：{data2[0, :, 0]}")
print(f"data2[0, :, :]：{data2[0, :, :]}")

代码输出：

data2：tensor([[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]],[[9, 6, 3, 1, 9],[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0]],[[6, 2, 7, 9, 7],[3, 3, 4, 3, 7],[0, 9, 0, 9, 6],[9, 5, 4, 8, 8]]])
data2[0, 0, 0]：2
data2[0, :, 0]：tensor([2, 5, 8, 2])
data2[0, :, :]：tensor([[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]])

七、张量的形状操作

在深度学习中，张量的形状（即维度结构）直接影响模型的计算逻辑和数据流动，因此灵活操作张量形状是处理数据和搭建模型的基础能力。

7.1 `np.reshape`

reshape()是PyTorch中最常用的张量形状调整函数之一，其核心功能是在不改变张量元素数量和值的前提下，重新定义张量的维度结构。这一操作类似于将相同数量的元素重新摆放到不同形状的容器中，元素本身不会发生变化，只是观察它们的维度视角改变了。

在深度学习中，reshape()常用于数据预处理和中间结果调整。例如，将卷积层输出的四维张量[batch, channel, height, width]重塑为全连接层需要的二维张量[batch, channel*height*width]，此时只需使用reshape(batch_size, -1)即可自动计算展开后的维度，非常便捷。

7.1.1 函数定义

reshape(array, shape, order='C')

功能：改变数组的维度结构（形状），而不改变其元素值和总元素个数。
参数：
- array：输入数组或可转换为数组的对象；
- shape：指定重塑后的新形状。若使用-1表示自动推断该维度的大小（必须保证其他维度能唯一确定-1的值）；
- order：指定元素读取和排列的顺序，取值包括：
  - 'C'（默认）：C风格顺序，行优先（最后一个维度变化最快）；
  - 'F'：Fortran风格顺序，列优先（第一个维度变化最快）；
  - 'A'：若原数组在内存中是Fortran连续的，则使用'F'顺序，否则使用'C'顺序；
  - 'K'：尽可能按照元素在内存中的出现顺序进行重塑。
返回值：一个形状为shape的新数组，其元素与原数组相同。若可能，返回的是原数组的视图（共享数据）；否则返回副本。总元素数量必须与原数组一致，否则抛出ValueError。

7.1.2 代码示例

data1 = torch.tensor([[10, 20, 30], [40, 50, 60]])
print(f"data1：{data1}")print(f"data1.shape：{data1.shape}")
print(f"data1.shape[0]：{data1.shape[0]}")
print(f"data1.shape[1]：{data1.shape[1]}")
print(f"data1.size：{data1.size()}")data1_new = data1.reshape(3, 2)
print(f"data1_new：{data1_new}")
data1_new_1 = data1.reshape(-1)
print(f"data1_new_1：{data1_new_1}")

代码输出：

data1：tensor([[10, 20, 30],[40, 50, 60]])
data1.shape：torch.Size([2, 3])
data1.shape[0]：2
data1.shape[1]：3
data1.size：torch.Size([2, 3])
data1_new：tensor([[10, 20],[30, 40],[50, 60]])
data1_new_1：tensor([10, 20, 30, 40, 50, 60])

7.2 `tensor.squeeze`和`tensor.unsqueeze`

squeeze()和unsqueeze()是一对功能互补的函数，专门用于处理张量中大小为1的维度（即单元素维度）。在深度学习中，这类维度常见于批量处理（如单样本的批量维度）、特征扩展等场景，合理使用这两个函数可以简化维度操作，避免冗余维度对计算的干扰。

7.2.1 函数定义

函数	函数签名	功能	参数说明	返回值
`squeeze()`	`tensor.squeeze(dim=None)`	移除张量中大小为1的维度。若指定`dim`，则仅压缩该维度；否则压缩所有可压缩维度。	- `dim`：要压缩的维度索引，必须大小为1。支持负索引，范围`[-ndim, ndim-1]`	新张量，形状为压缩后的结果，与原张量共享数据。
`unsqueeze()`	`tensor.unsqueeze(dim)`	在指定位置插入一个大小为1的新维度，维度总数加1。	- `dim`：插入新维度的位置。取值范围`[-ndim-1, ndim]`，支持负索引	新张量，形状为插入维度后的结果，与原张量共享数据。

7.3.2 代码示例

torch.random.manual_seed(42)
data2 = torch.randint(0, 10, [3, 4, 5])
print(f"data2：{data2}")data2_0 = data2.unsqueeze(dim=0)
print(f"data2_0：{data2_0}")
print(f"data2_0.shape：{data2_0.shape}")
data2_1 = data2.unsqueeze(dim=1)
print(f"data2_1：{data2_1}")
print(f"data2_1.shape：{data2_1.shape}")
data2_2 = data2.unsqueeze(dim=-1)
print(f"data2_2：{data2_2}")
print(f"data2_2.shape：{data2_2.shape}")data2_2_ = data2_2.squeeze()
print(f"data2_2_：{data2_2_}")
print(f"data2_2_.shape：{data2_2_.shape}")

代码输出：

data2：tensor([[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]],[[9, 6, 3, 1, 9],[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0]],[[6, 2, 7, 9, 7],[3, 3, 4, 3, 7],[0, 9, 0, 9, 6],[9, 5, 4, 8, 8]]])
data2_0：tensor([[[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]],[[9, 6, 3, 1, 9],[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0]],[[6, 2, 7, 9, 7],[3, 3, 4, 3, 7],[0, 9, 0, 9, 6],[9, 5, 4, 8, 8]]]])
data2_0.shape：torch.Size([1, 3, 4, 5])
data2_1：tensor([[[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]]],[[[9, 6, 3, 1, 9],[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0]]],[[[6, 2, 7, 9, 7],[3, 3, 4, 3, 7],[0, 9, 0, 9, 6],[9, 5, 4, 8, 8]]]])
data2_1.shape：torch.Size([3, 1, 4, 5])
data2_2：tensor([[[[2],[7],[6],[4],[6]],[[5],[0],[4],[0],[3]],[[8],[4],[0],[4],[1]],[[2],[5],[5],[7],[6]]],[[[9],[6],[3],[1],[9]],[[3],[1],[9],[7],[9]],[[2],[0],[5],[9],[3]],[[4],[9],[6],[2],[0]]],[[[6],[2],[7],[9],[7]],[[3],[3],[4],[3],[7]],[[0],[9],[0],[9],[6]],[[9],[5],[4],[8],[8]]]])
data2_2.shape：torch.Size([3, 4, 5, 1])
data2_2_：tensor([[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6]],[[9, 6, 3, 1, 9],[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0]],[[6, 2, 7, 9, 7],[3, 3, 4, 3, 7],[0, 9, 0, 9, 6],[9, 5, 4, 8, 8]]])
data2_2_.shape：torch.Size([3, 4, 5])

7.3 `torch.transpose`和`torch.permute`

在处理高维张量时，经常需要调整维度的顺序（如交换图像的通道和高度维度），torch.transpose和torch.permute是实现这一功能的核心函数。两者都用于维度重排，但适用场景不同：transpose()专注于交换两个维度，permute()则支持一次性重排所有维度。

两者的核心区别在于灵活性：transpose()一次只能交换两个维度，适合简单的维度调整（如矩阵转置，即交换二维张量的0维和1维）；permute()则可一次性重排所有维度，适合复杂的高维张量操作（如将图像张量的[batch, height, width, channel]转换为[batch, channel, height, width]）。

7.3.1 函数签名

（1）`torch.transpose`

torch.transpose(input, dim0, dim1)

功能：交换张量中指定的两个维度（轴），常用于矩阵转置或调整数据布局。该操作不修改原张量，仅返回一个视图。
参数说明：
- input：输入张量；
- dim0：第一个要交换的维度索引；
- dim1：第二个要交换的维度索引。支持负索引，dim0和dim1必须在有效范围内且不相等。
返回值：一个新的张量，其形状为dim0和dim1交换后的结果，与原张量共享数据。

（2）`torch.permute`

torch.permute(input, dims)

功能：对张量的维度进行任意顺序的重排（置换），支持多维张量的灵活轴变换。常用于将通道维度移到特定位置。
参数说明：
- input：输入张量；
- dims：指定输出张量各维度对应原张量的哪个维度，必须是原维度索引的一个排列。长度必须等于输入张量的维度数ndim。支持负索引，但通常使用非负索引更清晰。
返回值：一个新张量，其维度按dims指定的顺序重排，与原张量共享数据。

7.3.2 代码示例

torch.random.manual_seed(43)
data3 = torch.tensor(np.random.randint(0, 10, [4, 2, 3, 5]))
print(f"data3：{data3}")
print(f"data3.shape：{data3.shape}")
## 3.1 transpose
data3_t1 = torch.transpose(data3, 0, 2)
print(f"data3_t：{data3_t1}")
print(f"data3_t.shape：{data3_t1.shape}")
data3_t2 = data3_t1.transpose(1, 2)
data3_t3 = data3_t2.transpose(2, 3)
print(f"data3_t3：{data3_t3}")
print(f"data3_t3.shape：{data3_t3.shape}")
## 3.2 permute
data3_p1 = data3.permute(2, 0, 3, 1)
print(f"data3_p1：{data3_p1}")
print(f"data3_p1.shape：{data3_p1.shape}")

代码输出：

data3：tensor([[[[7, 4, 3, 0, 7],[6, 0, 7, 5, 0],[2, 4, 8, 6, 1]],[[9, 9, 7, 6, 7],[5, 4, 4, 2, 2],[0, 5, 6, 5, 4]]],[[[7, 4, 2, 4, 5],[4, 2, 8, 3, 5],[0, 4, 8, 2, 4]],[[1, 6, 6, 1, 9],[8, 6, 2, 7, 0],[1, 1, 9, 6, 4]]],[[[0, 9, 2, 4, 9],[7, 6, 2, 1, 6],[1, 4, 9, 1, 1]],[[0, 3, 7, 7, 1],[8, 0, 0, 8, 0],[1, 7, 6, 3, 8]]],[[[9, 6, 6, 5, 1],[4, 0, 2, 6, 1],[9, 5, 3, 9, 4]],[[9, 7, 8, 8, 7],[2, 7, 8, 9, 0],[1, 6, 1, 8, 4]]]], dtype=torch.int32)
data3.shape：torch.Size([4, 2, 3, 5])
data3_t：tensor([[[[7, 4, 3, 0, 7],[7, 4, 2, 4, 5],[0, 9, 2, 4, 9],[9, 6, 6, 5, 1]],[[9, 9, 7, 6, 7],[1, 6, 6, 1, 9],[0, 3, 7, 7, 1],[9, 7, 8, 8, 7]]],[[[6, 0, 7, 5, 0],[4, 2, 8, 3, 5],[7, 6, 2, 1, 6],[4, 0, 2, 6, 1]],[[5, 4, 4, 2, 2],[8, 6, 2, 7, 0],[8, 0, 0, 8, 0],[2, 7, 8, 9, 0]]],[[[2, 4, 8, 6, 1],[0, 4, 8, 2, 4],[1, 4, 9, 1, 1],[9, 5, 3, 9, 4]],[[0, 5, 6, 5, 4],[1, 1, 9, 6, 4],[1, 7, 6, 3, 8],[1, 6, 1, 8, 4]]]], dtype=torch.int32)
data3_t.shape：torch.Size([3, 2, 4, 5])
data3_t3：tensor([[[[7, 9],[4, 9],[3, 7],[0, 6],[7, 7]],[[7, 1],[4, 6],[2, 6],[4, 1],[5, 9]],[[0, 0],[9, 3],[2, 7],[4, 7],[9, 1]],[[9, 9],[6, 7],[6, 8],[5, 8],[1, 7]]],[[[6, 5],[0, 4],[7, 4],[5, 2],[0, 2]],[[4, 8],[2, 6],[8, 2],[3, 7],[5, 0]],[[7, 8],[6, 0],[2, 0],[1, 8],[6, 0]],[[4, 2],[0, 7],[2, 8],[6, 9],[1, 0]]],[[[2, 0],[4, 5],[8, 6],[6, 5],[1, 4]],[[0, 1],[4, 1],[8, 9],[2, 6],[4, 4]],[[1, 1],[4, 7],[9, 6],[1, 3],[1, 8]],[[9, 1],[5, 6],[3, 1],[9, 8],[4, 4]]]], dtype=torch.int32)
data3_t3.shape：torch.Size([3, 4, 5, 2])
data3_p1：tensor([[[[7, 9],[4, 9],[3, 7],[0, 6],[7, 7]],[[7, 1],[4, 6],[2, 6],[4, 1],[5, 9]],[[0, 0],[9, 3],[2, 7],[4, 7],[9, 1]],[[9, 9],[6, 7],[6, 8],[5, 8],[1, 7]]],[[[6, 5],[0, 4],[7, 4],[5, 2],[0, 2]],[[4, 8],[2, 6],[8, 2],[3, 7],[5, 0]],[[7, 8],[6, 0],[2, 0],[1, 8],[6, 0]],[[4, 2],[0, 7],[2, 8],[6, 9],[1, 0]]],[[[2, 0],[4, 5],[8, 6],[6, 5],[1, 4]],[[0, 1],[4, 1],[8, 9],[2, 6],[4, 4]],[[1, 1],[4, 7],[9, 6],[1, 3],[1, 8]],[[9, 1],[5, 6],[3, 1],[9, 8],[4, 4]]]], dtype=torch.int32)
data3_p1.shape：torch.Size([3, 4, 5, 2])

7.4 `tensor.view`和`tensor.contiguous`

view()和contiguous()是与张量内存布局密切相关的两个函数。view()用于重塑张量形状，但其功能受限于张量的连续性；contiguous()则用于确保张量在内存中连续存储，为view()等操作提供支持。理解这两个函数需要先明确张量连续性的概念。

7.4.1 函数定义

（1）`tensor.view`

tensor.view(*shape)

功能：用于改变张量的形状，但不改变其底层数据。它返回一个与原张量共享数据的新张量，形状由shape指定。该操作要求张量在内存中是连续的，否则会抛出错误。
参数说明：
- *shape：指定新形状的维度大小。支持使用-1表示自动推断该维度的大小（只能出现一次）。新形状的总元素数量必须与原张量一致。
返回值：一个形状为指定shape的新张量，与原张量共享数据。若原张量非连续，则调用view()会失败并抛出RuntimeError。

（2）`tensor.contiguous`

tensor.contiguous(memory_format=torch.contiguous_format)

功能：返回一个在内存中连续存储的张量副本。如果原张量已经是连续的，则返回其本身（不复制数据）；否则，会复制数据以确保内存布局连续。该方法常用于在调用view()前确保张量连续。
参数说明：
- memory_format：指定输出张量的内存格式：
  - torch.contiguous_format（默认）：行优先（C-style）连续；
  - torch.channels_last：用于图像数据的通道最后格式。
返回值：一个内存连续的张量。若原张量已连续，则返回原张量的视图；否则返回一个新的连续副本。

7.4.2 代码示例

torch.random.manual_seed(44)
data4 = torch.randint(0, 10, [2, 3])
print(f"data4：{data4}")
print(f"判断data4是否连续：{data4.is_contiguous()}")
print(f"修改data4的形状为(-1)：{data4.view(-1)}")data4_t1 = data4.transpose(0, 1)
print(f"判断data4_t1是否连续：{data4_t1.is_contiguous()}")
data4_t1_c = data4_t1.contiguous()
print(f"判断data4_t1_c是否连续：{data4_t1_c.is_contiguous()}")
print(f"修改data4_t1_c的形状为(-1)：{data4_t1_c.view(-1)}")

代码输出：

data4：tensor([[2, 3, 7],[5, 3, 9]])
判断data4是否连续：True
修改data4的形状为(-1)：tensor([2, 3, 7, 5, 3, 9])
判断data4_t1是否连续：False
判断data4_t1_c是否连续：True
修改data4_t1_c的形状为(-1)：tensor([2, 5, 3, 3, 7, 9])

八、张量的拼接操作

在深度学习中，我们经常需要将多个张量组合成一个更大的张量来进行后续计算。例如，在处理批量数据时，可能需要将不同批次的样本拼接在一起；在特征融合时，可能需要将不同来源的特征张量合并为一个完整的特征矩阵。张量的拼接操作正是为了解决这类问题而设计的，它能够在不改变张量内部数据的前提下，按照指定维度将多个结构兼容的张量粘在一起。PyTorch中提供了cat()函数来实现这一功能，掌握它的使用方法对于高效处理张量数据至关重要。

8.1 函数定义

torch.cat(tensors, dim=0, *, out=None)

功能：沿指定维度将一个张量序列进行连接操作。输入张量在除拼接维度外的所有维度上必须具有相同的形状。拼接后，该维度的大小为所有输入张量在该维度上大小的总和。
参数：
- tensors：要拼接的张量序列（如list或tuple）。所有张量必须具有相同的形状，除了在dim指定的维度上；
- dim：指定拼接操作所沿的维度。默认为0（第一个维度）。支持负索引，取值范围为[-ndim, ndim-1]，其中ndim是输入张量的维度数；
- out：可选的输出张量，用于存储结果。其形状必须与预期输出完全匹配。
返回值：一个新的张量，其形状与输入张量相同，除了dim维度的大小为所有输入张量在该维度上的大小之和。该张量不共享输入张量的数据（是独立的副本）。

8.2 代码示例

import torchtorch.random.manual_seed(41)
data1 = torch.randint(0, 10, [4, 5, 3])
print(f"data1：{data1}")torch.random.manual_seed(42)
data2 = torch.randint(0, 10, [4, 5, 5])
print(f"data2：{data2}")print(f"dim=2：{torch.cat([data1, data2], dim=2)}")# 1×. 除拼接维度外，其余维度必须相同
# print(f"dim=1：{torch.cat([data1, data2], dim=1)}")
# # RuntimeError: Sizes of tensors must match except in dimension 1. Expected size 3 but got size 5 for tensor number 1 in the list.

代码输出：

data1：tensor([[[6, 3, 4],[0, 2, 7],[9, 5, 1],[5, 6, 5],[0, 2, 3]],[[9, 8, 4],[8, 0, 6],[7, 1, 5],[2, 8, 3],[2, 0, 9]],[[0, 5, 9],[6, 8, 9],[6, 9, 1],[1, 5, 8],[9, 6, 6]],[[8, 7, 1],[4, 4, 6],[3, 2, 1],[2, 1, 3],[3, 2, 6]]])
data2：tensor([[[2, 7, 6, 4, 6],[5, 0, 4, 0, 3],[8, 4, 0, 4, 1],[2, 5, 5, 7, 6],[9, 6, 3, 1, 9]],[[3, 1, 9, 7, 9],[2, 0, 5, 9, 3],[4, 9, 6, 2, 0],[6, 2, 7, 9, 7],[3, 3, 4, 3, 7]],[[0, 9, 0, 9, 6],[9, 5, 4, 8, 8],[6, 0, 0, 0, 0],[1, 3, 0, 1, 1],[7, 9, 4, 3, 8]],[[9, 3, 7, 8, 1],[4, 1, 6, 3, 2],[0, 9, 8, 5, 3],[7, 7, 5, 9, 1],[5, 1, 9, 1, 4]]])
dim=2：tensor([[[6, 3, 4, 2, 7, 6, 4, 6],[0, 2, 7, 5, 0, 4, 0, 3],[9, 5, 1, 8, 4, 0, 4, 1],[5, 6, 5, 2, 5, 5, 7, 6],[0, 2, 3, 9, 6, 3, 1, 9]],[[9, 8, 4, 3, 1, 9, 7, 9],[8, 0, 6, 2, 0, 5, 9, 3],[7, 1, 5, 4, 9, 6, 2, 0],[2, 8, 3, 6, 2, 7, 9, 7],[2, 0, 9, 3, 3, 4, 3, 7]],[[0, 5, 9, 0, 9, 0, 9, 6],[6, 8, 9, 9, 5, 4, 8, 8],[6, 9, 1, 6, 0, 0, 0, 0],[1, 5, 8, 1, 3, 0, 1, 1],[9, 6, 6, 7, 9, 4, 3, 8]],[[8, 7, 1, 9, 3, 7, 8, 1],[4, 4, 6, 4, 1, 6, 3, 2],[3, 2, 1, 0, 9, 8, 5, 3],[2, 1, 3, 7, 7, 5, 9, 1],[3, 2, 6, 5, 1, 9, 1, 4]]])

九、自动微分模块

在深度学习中，模型训练的核心是通过反向传播算法不断调整参数以最小化损失函数，而这一过程的关键在于高效计算损失函数对各个参数的梯度。手动推导和计算梯度不仅繁琐易错，还难以应对复杂模型（如深度神经网络）的需求。PyTorch的自动微分（Automatic Differentiation）模块正是为解决这一问题而设计的，它能够自动追踪张量的计算过程，并在需要时高效计算梯度，极大简化了模型训练的实现流程。自动微分是PyTorch等深度学习框架的核心功能之一，理解其原理和使用方法是掌握模型训练的基础。

9.1 含义

自动微分是一种介于数值微分（通过有限差分近似）和符号微分（通过数学公式推导）之间的梯度计算方法，它结合了两者的优点：既能够处理复杂的非线性函数，又能保证计算效率和精度。其核心思想是将复杂函数分解为一系列简单的基本运算（如加减乘除、三角函数、指数函数等），并记录这些运算的执行顺序（形成计算图），然后根据链式法则从输出反向推导出每个输入的梯度。
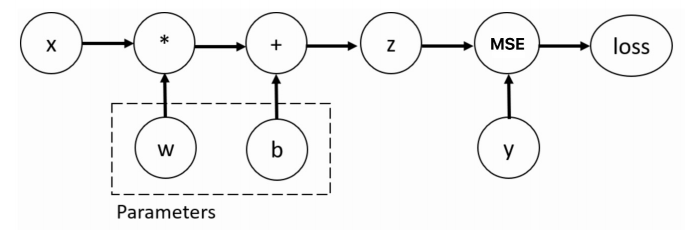
在这里插入图片描述

在深度学习中，自动微分的流程可分为两个阶段：

前向传播（Forward Pass）：在这一阶段，PyTorch会追踪所有涉及张量的运算，并构建一个计算图。计算图中的节点代表张量，边代表运算操作。只有当张量的requires_grad属性被设置为True时，PyTorch才会追踪其相关运算（默认值为False），这些张量通常是模型的可学习参数（如权重w和偏置b）。
反向传播（Backward Pass）：当我们对损失函数调用backward()方法时，PyTorch会从计算图的输出节点（损失值）出发，根据链式法则反向遍历计算图，自动计算损失函数对所有requires_grad=True的张量的梯度，并将结果存储在这些张量的grad属性中。

与其他梯度计算方法相比，自动微分的优势显著：

相比数值微分，它避免了截断误差（有限差分近似带来的误差），计算精度更高。
相比符号微分，它不会产生冗余的中间表达式，计算效率更高，且能自然支持控制流（如循环、条件判断）
对于深度学习中的复杂模型（如包含数百万参数的神经网络），自动微分能在毫秒级时间内完成梯度计算，这是手动计算无法实现的。

9.2 代码示例

import torch# 1. 初始化数据--特征+目标
X = torch.tensor(5)
Y = torch.tensor(0.)
# 2. 初始化参数--权重+偏置
w = torch.tensor(1, requires_grad=True, dtype=torch.float32)
b = torch.tensor(3, requires_grad=True, dtype=torch.float32)
# 3. 预测
z = w*X + b
# 4. 损失
loss = torch.nn.MSELoss()
loss = loss(z, Y)
# 5. 微分
loss.backward()
# 6. 梯度
print(f"w.grad：{w.grad}")
print(f"b.grad：{b.grad}")print('--'*50)
# 1. 初始化数据--特征+目标
x = torch.ones(2, 5)
y = torch.ones(2, 3)
# 2. 初始化参数--权重+偏置
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
# 3. 预测
z = torch.matmul(x, w) + b
# 4. 损失
loss = torch.nn.MSELoss()
loss = loss(z, y)
# 5. 微分
loss.backward()
# 6. 梯度
print(f"w.grad：{w.grad}")
print(f"b.grad：{b.grad}")

代码输出：

w.grad：80.0
b.grad：16.0
----------------------------------------------------------------------------------------------------
w.grad：tensor([[ 1.5318,  1.4443, -1.1252],[ 1.5318,  1.4443, -1.1252],[ 1.5318,  1.4443, -1.1252],[ 1.5318,  1.4443, -1.1252],[ 1.5318,  1.4443, -1.1252]])
b.grad：tensor([ 1.5318,  1.4443, -1.1252])

代码解析：

单变量线性模型的梯度计算：
参数定义：w和b的requires_grad=True是自动微分的核心开关。这一设置告诉PyTorch：请追踪所有涉及这两个张量的运算，以便后续计算梯度。而输入X和目标Y未设置该属性，因此它们的运算不会被追踪，也无需计算梯度；
前向传播与计算图构建：执行 $z = w * X + b$ 时，PyTorch会暗中构建计算图：节点包括w、X、b、z，边包括乘法 $w * X$ 和加法 $+ b$ 。此时计算图仅记录运算顺序，不计算梯度；
损失计算： $loss = (z - Y)^2$ 是一个标量（单个数值），它是计算图的最终输出节点。在深度学习中，损失函数的输出必须是标量才能调用backward()；
反向传播与梯度计算：loss.backward()会触发从损失节点到w和b的反向遍历。根据链式法则：
损失对z的梯度为 $d l oss / d z = 2 * (z - Y) = 2 * (8 - 0) = 16$ ；
损失对w的梯度为 $d l oss / d w = d l oss / d z * d z / d w = 16 * X = 16 * 5 = 80$ ，对应输出w.grad：80.0；
损失对b的梯度为 $d l oss / d b = d l oss / d z * d z / d b = 16 * 1 = 16$ ，对应输出b.grad：16.0。

梯度存储：计算得到的梯度会自动存入w.grad和b.grad中，这些梯度将用于后续的参数更新。

多变量矩阵运算的梯度计算：
高维张量支持：与1的标量运算不同，该示例使用矩阵运算模拟实际深度学习场景（批量样本输入）。x是[2,5]的特征矩阵（2个样本），w是[5,3]的权重矩阵（将5维特征映射到3维输出），通过torch.matmul(x, w)得到[2,3]的预测值z，再加上[3]的偏置b（自动广播为[2,3]）；
损失计算的批量处理：MSELoss默认会对批量样本的损失取平均值，最终得到标量损失，确保backward()可正常调用；
梯度的形状一致性：输出的w.grad形状与w相同[5,3]，b.grad形状与b相同[3]。这是因为梯度的形状必须与参数一致，才能用于参数更新。观察输出可发现，w.grad的每一行都相同，这是因为x是全1矩阵，批量样本的梯度叠加后呈现规律性；
自动广播的梯度处理：偏置b在计算中被广播为[2,3]，但反向传播时PyTorch会自动处理广播带来的维度扩展，确保b.grad的形状正确，无需手动调整。

十、综合实战——线性回归

线性回归是机器学习和深度学习中的基础模型，它通过拟合线性函数来描述输入特征与目标值之间的关系。在深度学习框架中，线性回归不仅是入门级实战案例，更能帮助理解数据准备→模型构建→训练优化→结果评估的完整流程。

10.1 基本流程

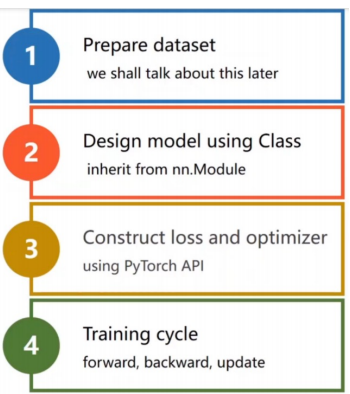
在这里插入图片描述

线性回归的实战流程可概括为数据→模型→训练→评估四大环节，每个环节紧密衔接，共同构成模型从构建到应用的完整生命周期。具体步骤如下：

数据准备：包括数据集创建（或加载）、数据预处理（如格式转换、归一化）、数据集划分（训练集/测试集）。对于线性回归，通常需要特征数据（输入x）和对应的目标值（输出y），且两者需满足近似线性关系。
数据加载：使用数据加载工具（如PyTorch的DataLoader）将数据按批次batch加载，同时支持数据打乱shuffle，以避免模型学习到数据的顺序规律，提高泛化能力。
模型定义：构建线性回归模型，即定义线性函数 $y = w x + b$ 。在PyTorch中，可直接使用nn.Linear层实现，该层会自动初始化权重w和偏置b，并支持自动微分。
损失函数与优化器：选择合适的损失函数（线性回归常用均方误差MSE）衡量预测值与真实值的差异；选择优化器（如随机梯度下降SGD）根据损失的梯度更新模型参数w和b。
模型训练：通过多轮迭代epoch完成训练：
- 前向传播：将输入数据传入模型，得到预测值；
- 损失计算：用损失函数计算预测值与真实值的差异；
- 反向传播：调用backward()计算损失对参数的梯度；
- 参数更新：优化器根据梯度调整参数（如 $\times w.grad$ ），同时清零本轮梯度，避免累积。
模型评估与可视化：训练结束后，通过损失变化曲线判断模型是否收敛；绘制拟合直线与原始数据的对比图，直观展示模型效果。

10.2 代码实战

10.2.1 导入工具包

import torch
from torch.utils.data import TensorDataset # 构造数据集对象
from torch.utils.data import DataLoader # 数据加载器
from torch import nn # nn模块中有平方损失函数和假设函数
from torch import optim # optim模块中有优化器函数
from sklearn.datasets import make_regression # 创建线性回归模型数据集
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

10.2.2 构建数据集

x, y, coef = make_regression(n_samples=100, # 样本数量n_features=1, # 特征数量noise=10, # 噪声bias=1.5, # 截距coef=True # 是否返回系数
)plt.scatter(x, y)
plt.show()

代码输出：
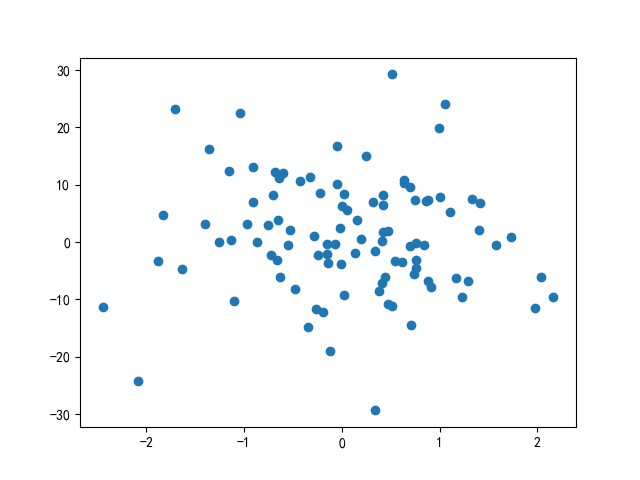
代码解析：

参数说明：
n_samples=100：生成100个样本，样本数量需适中（过少可能导致过拟合，过多会增加计算成本）；
n_features=1：每个样本包含1个特征，即单变量线性回归（便于二维可视化）；
noise=10：添加噪声（服从正态分布的随机值），模拟真实数据中的干扰因素，使数据点不完全落在直线上，更贴近实际场景；
bias=1.5：真实模型的截距，即b=1.5，生成的目标值满足 $\times x + bias + noise$ ；
coef=True：返回真实的权重系数w，用于后续与模型训练结果对比。

数据可视化：plt.scatter(x, y)绘制散点图，横轴为特征x，纵轴为目标值y。从输出图像可观察到：数据点大致沿某条直线分布，但因噪声存在而略有偏离，这符合线性回归的适用场景（输入与输出存在线性趋势）。

10.2.3 构建数据集加载器

## 3.1 数据转换
x = torch.tensor(x)
y = torch.tensor(y)
## 3.2 构建torch数据集
dataset = TensorDataset(x, y)
## 3.3 构建batch数据
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)

代码解析：

3.1 数据转换：torch.tensor(x)将NumPy数组转换为PyTorch张量。PyTorch的模型运算依赖张量（支持自动微分、GPU加速等），因此这一步是必要的。转换后，x和y的类型从numpy.ndarray变为torch.Tensor；
3.2 构建数据集对象：TensorDataset(x, y)将特征x和目标值y按样本绑定为数据集对象；
3.3 构建数据加载器：
dataset：传入上述构建的数据集对象；
batch_size=2：每次加载2个样本进行训练（批量训练可提高计算效率，同时利用梯度下降的随机性避免局部最优）；
shuffle=True：每个epoch训练前打乱数据顺序，避免模型学习到样本的排列规律。

10.2.4 构建模型

model = torch.nn.Linear(in_features=1, # 输入特征数量out_features=1 # 输出特征数量
)

10.2.5 训练模型

## 5.1 定义损失函数
mse = torch.nn.MSELoss()
## 5.2 定义优化器
optimizer = torch.optim.SGD(params=model.parameters(), lr=0.01)
## 5.3 模型训练
loss_sum = []
for epoch in range(100):sum = 0sample = 0for x, y in dataloader:# 模型预测y_pred = model(x.type(torch.float32))# 计算损失loss = mse(y_pred, y.reshape(-1, 1).type(torch.float32))sum += loss.item()sample += len(y)# 梯度清零optimizer.zero_grad()# 反向传播loss.backward()# 优化器更新参数optimizer.step()loss_sum.append(sum / sample)

代码解析：

5.1 损失函数：nn.MSELoss()定义均方误差损失函数，计算公式为： $loss=1n∑i=1n(y^i−yi)2\text{loss} = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2$ ，其中 $y^\hat{y}$ 是预测值， $y$ 是真实值。MSELoss对误差进行平方惩罚，对较大误差更敏感，适合线性回归场景。
5.2 优化器：optim.SGD是随机梯度下降优化器，参数包括：
params=model.parameters()：指定需要优化的参数（模型的w和b）；
lr=0.01：学习率（步长），控制参数更新的幅度（过大会导致不收敛，过小会导致训练缓慢）。

5.3 训练循环：
外层循环（epoch）：共执行100轮训练，每轮遍历整个数据集一次。loss_sum记录每轮的平均损失，用于后续绘制收敛曲线；
内层循环（batch）：通过dataloader按批次加载数据，每次处理batch_size=2个样本：
模型预测：model(x.type(torch.float32))将输入张量转换为float32类型（与模型参数类型一致），得到预测值y_pred；
损失计算：y.reshape(-1, 1)将目标值调整为与y_pred相同的形状[batch_size, 1]，避免维度不匹配错误；loss.item()将损失张量转换为Python数值，便于累加；
梯度清零：optimizer.zero_grad()清空上一轮的梯度（PyTorch默认累积梯度，若不清零会导致梯度叠加，影响参数更新）；
反向传播：loss.backward()自动计算损失对w和b的梯度，并存储在w.grad和b.grad中；
参数更新：optimizer.step()根据梯度和学习率更新参数（如 $\times w.grad$ ）。

10.2.6 预测模型

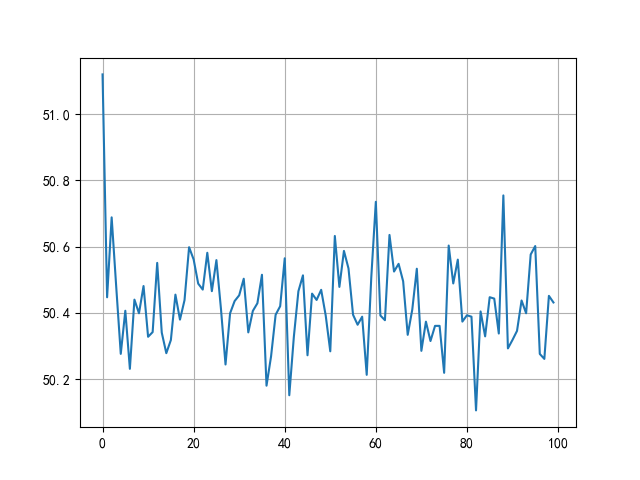
## 6.1 绘制损失变化曲线
plt.plot(range(100), loss_sum)
plt.grid()
plt.show()
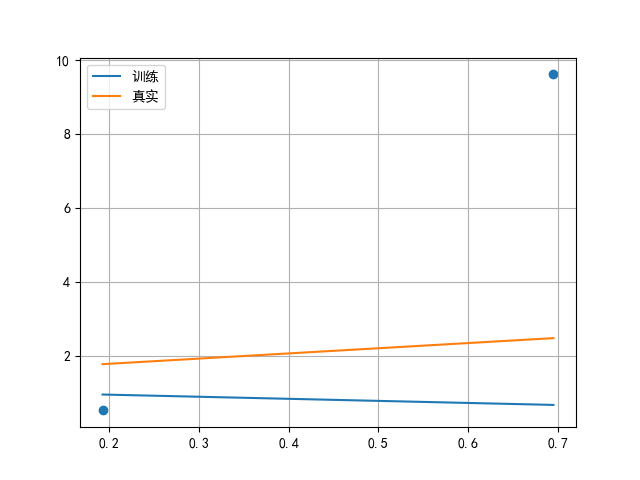
## 6.2 绘制拟合直线
plt.scatter(x, y)
x = torch.linspace(x.min(), x.max(), 1000)
y1 = torch.tensor([v * model.weight + model.bias for v in x])
y2 = torch.tensor([v * coef + 1.5 for v in x])
plt.plot(x, y1, label='训练')
plt.plot(x, y2, label='真实')
plt.grid()
plt.legend()
plt.show()

代码输出：
代码解析：

6.1 损失变化曲线：plt.plot(range(100), loss_sum)绘制100轮训练的平均损失曲线。从输出图像可见：损失随epoch增加逐渐下降并趋于稳定，说明模型在不断优化，最终收敛到较低的损失值（曲线趋于平缓）。若曲线未收敛（持续下降或波动），可能需要增加epoch数量或调整学习率；
6.2 拟合直线对比：
plt.scatter(x, y)再次绘制原始数据点，作为参考；
torch.linspace(x.min(), x.max(), 1000)生成从特征最小值到最大值的1000个均匀点，用于绘制连续的拟合直线；
y1是模型的预测直线：通过训练后的model.weight（优化后的w）和model.bias（优化后的b）计算，即 $w_{\text{训练}} \times x + b_{\text{训练}}$ ；
y2是真实直线：使用make_regression返回的coef（真实w）和bias=1.5（真实b）计算，即 $w_{\text{真实}} \times x + b_{\text{真实}}$ ；
两条直线的对比直观展示模型的拟合效果：训练直线与真实直线越接近，说明模型效果越好。