【LeetCode热题100道笔记+动画】乘积最大子数组
题目描述
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续 子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
- 1<=nums.length<=2∗1041 <= nums.length <= 2 * 10^41<=nums.length<=2∗104
- −10<=nums[i]<=10-10 <= nums[i] <= 10−10<=nums[i]<=10
- nums 的任何子数组的乘积都 保证 是一个 32-位 整数
思考
针对含负数的数组,最大乘积子数组需同时追踪“最大乘积”和“最小乘积”:
- 负数特性导致:最小乘积(可能为负)× 负数 可能变为最大乘积
- 用动态规划维护两个状态数组,分别记录以每个位置结尾的最大/最小乘积
算法过程
-
初始化:
dpMax[i]:以第i个元素结尾的子数组的最大乘积dpMin[i]:以第i个元素结尾的子数组的最小乘积- 初始值:
dpMax[0] = dpMin[0] = nums[0](首个元素自身构成子数组) - 结果变量
result初始化为nums[0]
-
遍历更新(i从1到n-1):
- 计算当前位置的最大乘积:
dpMax[i] = max(dpMax[i-1]×nums[i], dpMin[i-1]×nums[i], nums[i]) - 计算当前位置的最小乘积:
dpMin[i] = min(dpMin[i-1]×nums[i], dpMax[i-1]×nums[i], nums[i]) - 更新全局结果:
result = max(result, dpMax[i])
- 计算当前位置的最大乘积:
-
返回结果:最终
result即为最大乘积子数组的乘积
时间复杂度
- 时间复杂度:O(n),仅遍历数组一次(n为数组长度)
- 空间复杂度:O(n),使用两个长度为n的状态数组(可优化为O(1),只需保留前一位置的最大/最小值)
该方法通过同时追踪最大和最小乘积,完整覆盖了负数带来的乘积反转情况,确保找到全局最大乘积。
代码一
/*** @param {number[]} nums* @return {number}*/
var maxProduct = function(nums) {const n = nums.length;const dpMax = Array(n).fill(-Infinity);const dpMin = Array(n).fill(-Infinity);dpMax[0] = nums[0];dpMin[0] = nums[0];let result = nums[0]; for (let i = 1; i < n; i++) {dpMax[i] = Math.max(dpMax[i-1] * nums[i], dpMin[i-1] * nums[i], nums[i]);dpMin[i] = Math.min(dpMin[i-1] * nums[i], dpMax[i-1] * nums[i], nums[i]);result = Math.max(dpMax[i], dpMin[i], result);}return result;
};
代码二:优化O(1)空间
/*** @param {number[]} nums* @return {number}*/
var maxProduct = function(nums) {const n = nums.length;let preMax = nums[0], preMin = nums[0], result = nums[0]; for (let i = 1; i < n; i++) {let curMax = Math.max(preMax * nums[i], preMin * nums[i], nums[i]);let curMin = Math.min(preMax * nums[i], preMin * nums[i], nums[i]);result = Math.max(curMax, curMin, result);preMax = curMax;preMin = curMin;}return result;
};
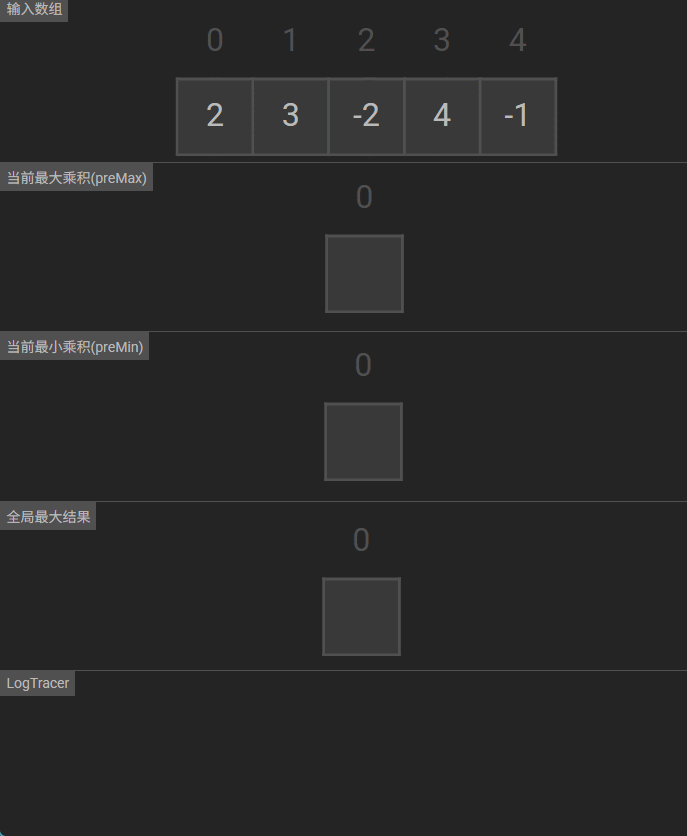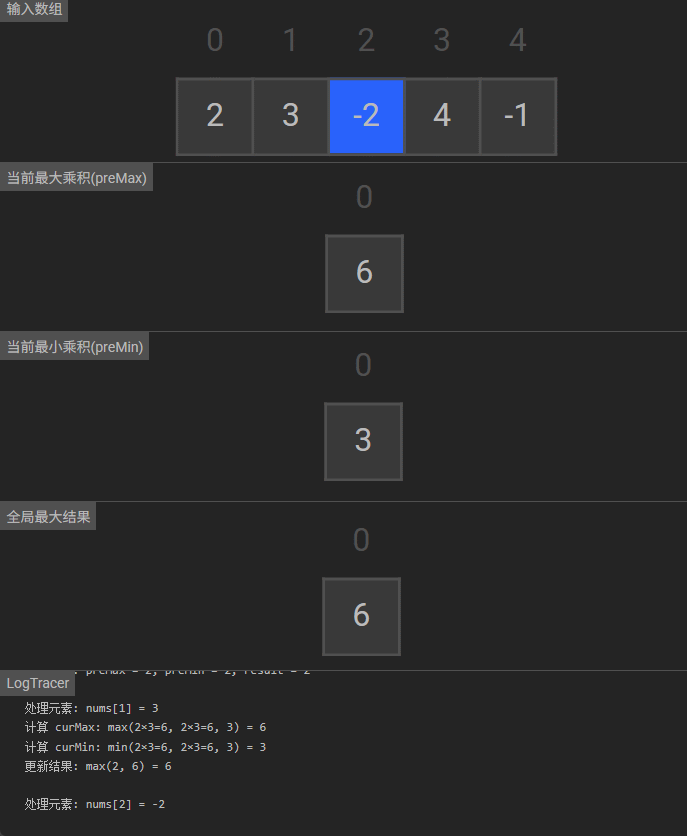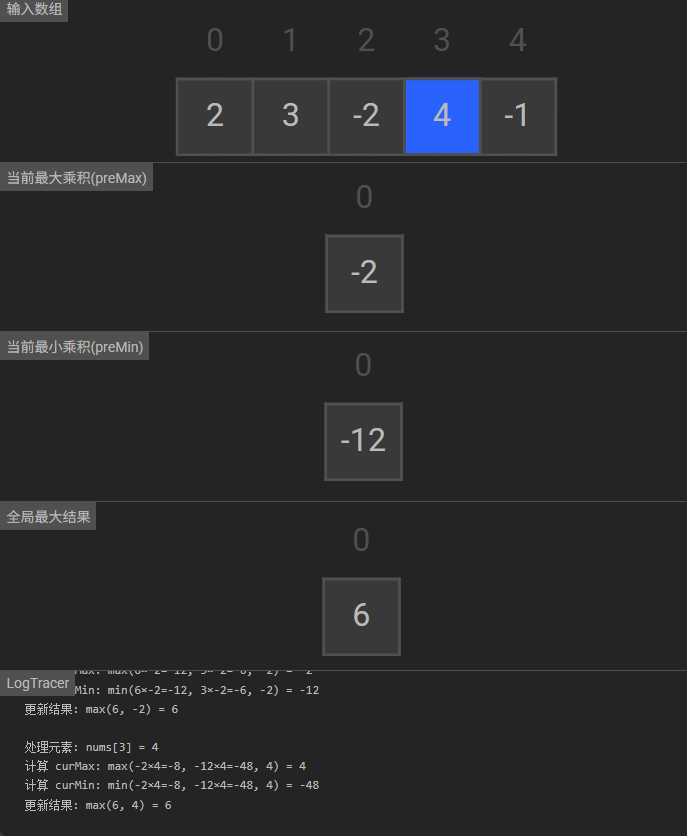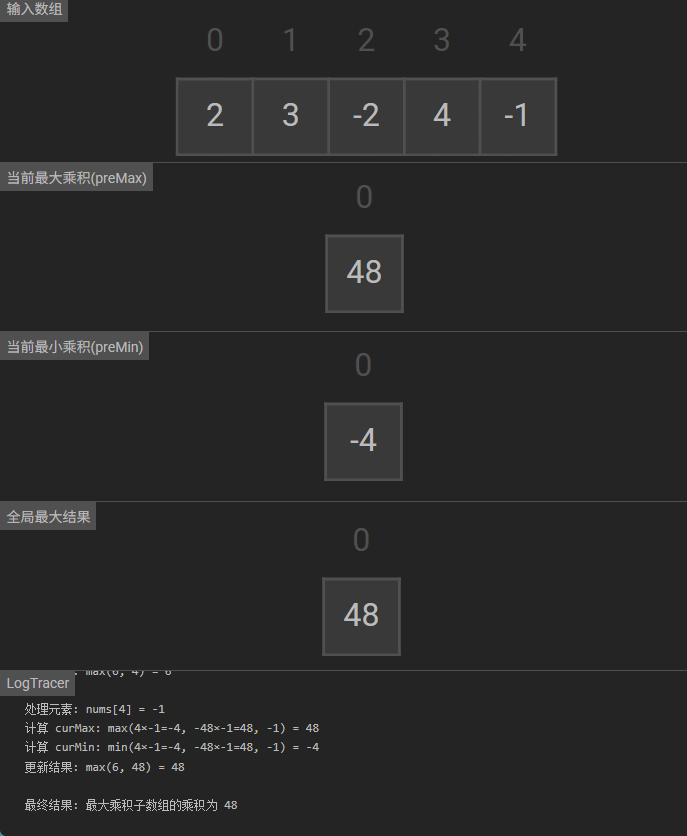
可视化