Swin Transformer基本原理与传统Transformer对比图解
目录
一 Swin Transformer 核心创新
二 窗口注意力 (Window Attention)
2.1.1为什么需要窗口注意力?
2.1.2 窗口注意力的核心原理
2.1.3 优势
2.1.4示例理解
2.1.5 传统注意力 vs 窗口注意力
2.1.1.6 计算复杂度对比
三 移位窗口 (Shifted Window)
3.1.1原始窗口(蓝色) vs 移位窗口(紫色)
3.1.2 Swin Transformer 层级结构
四 性能对比
一 Swin Transformer 核心创新
Swin Transformer 是一种基于Transformer的视觉识别模型,其核心创新在于引入了窗口注意力(Window Attention)和移位窗口(Shifted Window)机制,解决了传统Transformer在处理高分辨率图像时计算复杂度高的问题。

二 窗口注意力 (Window Attention)
2.1.1为什么需要窗口注意力?
传统 Transformer 的自注意力机制需要计算所有像素(或图像补丁)之间的依赖关系,计算复杂度为 O(N²)(N 为像素 / 补丁总数)。当处理高分辨率图像(如 224×224 甚至更大)时,N 会非常大(例如 224×224 图像分割为 16×16 补丁后,N=196),此时 O (N²) 的计算量会急剧增加,导致模型效率极低,难以应用于实际视觉任务。
2.1.2 窗口注意力的核心原理
窗口注意力通过以下方式优化计算:
-
图像分窗:将输入图像(或特征图)分割为若干个不重叠的局部窗口(例如 7×7 大小的窗口)。
假设图像被分割为 H×W 个补丁,窗口大小为 W×W,则整个图像会被划分为 (H/W)×(W/W) 个独立窗口。 -
局部注意力计算:仅在每个窗口内部计算自注意力,而不考虑窗口外的像素 / 补丁。
此时,每个窗口内的注意力计算复杂度为 O (W²)(窗口内补丁数量为 W²),而全局总计算复杂度变为 O ((H×W/W²) × W²) = O (H×W × W²) = O (N×W²)(N=H×W 为总补丁数)。
2.1.3 优势
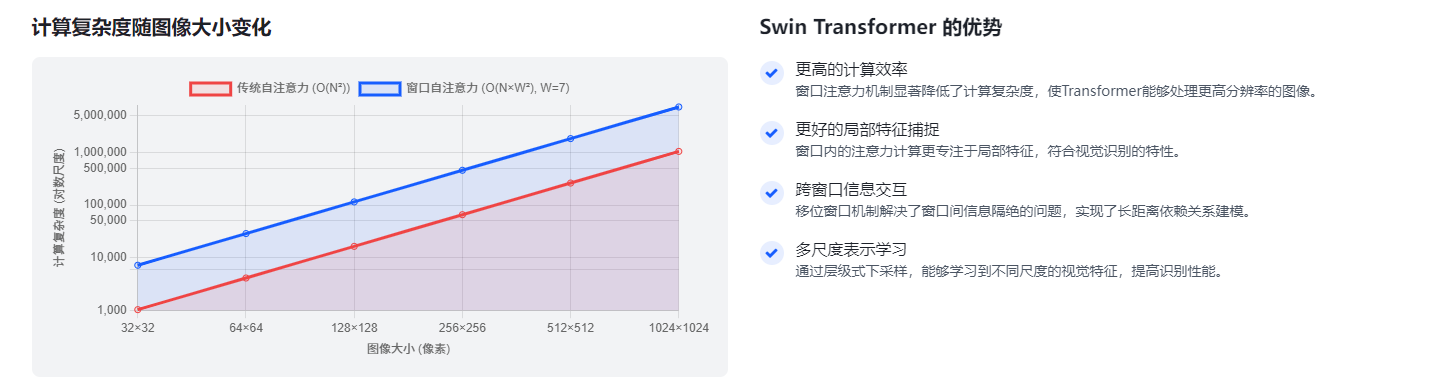
- 效率大幅提升:计算复杂度从 O (N²) 降至 O (N×W²),当窗口大小 W 固定(如 7)时,复杂度随图像尺寸呈线性增长(而非平方级),使模型能处理更高分辨率的图像。
- 符合视觉特性:视觉任务中,物体的局部特征(如纹理、边缘)往往比全局特征更重要,窗口内的局部注意力更符合视觉信号的局部相关性。
2.1.4示例理解
假设一幅图像被分割为 28×28 个补丁(共 784 个,即 N=784),使用 7×7 的窗口:
- 传统自注意力:需计算 784×784≈61.5 万对依赖关系;
- 窗口注意力:图像被分为 4×4=16 个窗口(每个窗口 7×7=49 个补丁),总计算量为 16×49×49≈3.8 万对,仅为传统方式的 6%。
传统Transformer在处理图像时,需要计算所有像素之间的注意力,计算复杂度为O(N²),其中N是图像的像素数量。当图像分辨率较高时,这种计算方式变得非常低效。
Swin Transformer提出了窗口注意力机制,将图像分割成多个不重叠的窗口,仅在每个窗口内计算注意力。这种方式将计算复
2.1.5 传统注意力 vs 窗口注意力
传统注意力:所有像素间计算注意力
窗口注意力:仅在窗口内计算注意力
杂度降至O(NW²),其中W是窗口大小,显著提高了计算效率。

2.1.1.6 计算复杂度对比
假设图像被分割为H×W的补丁(patches),则:
三 移位窗口 (Shifted Window)
窗口注意力虽然提高了计算效率,但也带来了新的问题:窗口之间的信息无法交互。为了解决这个问题,Swin Transformer引入了移位窗口机制,通过在下一层将窗口偏移一定距离,让相邻窗口产生重叠,从而实现跨窗口的信息交互。
3.1.1原始窗口(蓝色) vs 移位窗口(紫色)
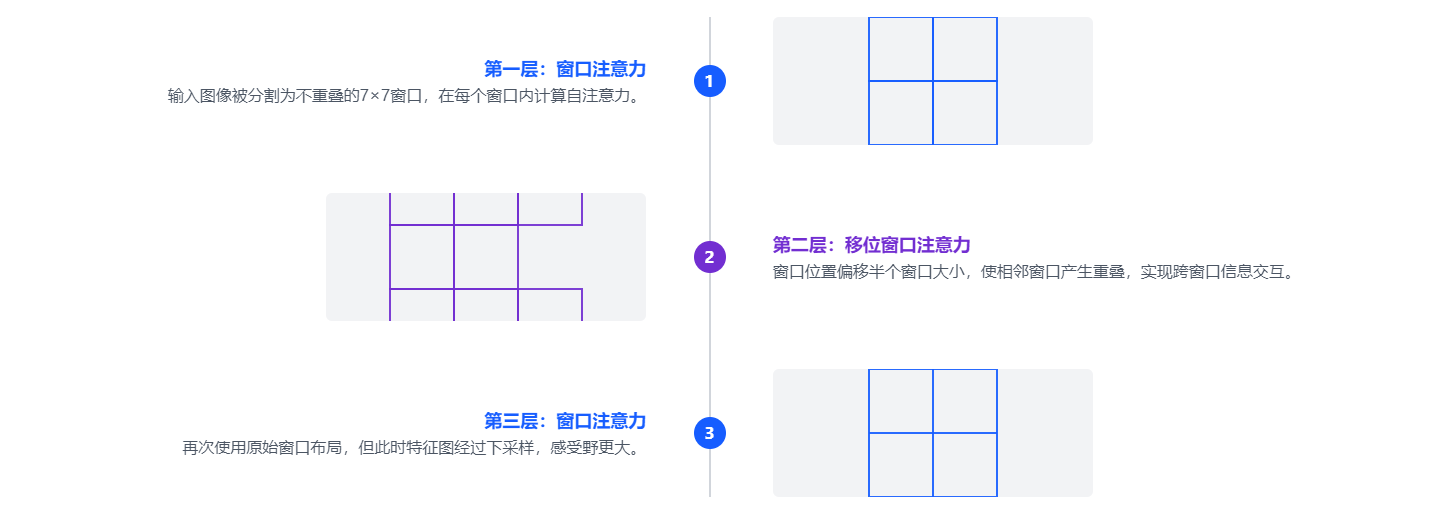
移位窗口机制通过将窗口位置偏移半个窗口大小,使得原本分离的窗口产生重叠,从而允许跨窗口的信息流动。

3.1.2 Swin Transformer 层级结构
四 性能对比