LeetCode54螺旋矩阵算法详解

螺旋矩阵算法详解

题目描述

给你一个 m 行 n 列的矩阵 matrix，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]可视化：
1 → 2 → 3↓
4 → 5   6
↑       ↓
7 ← 8 ← 9

算法核心思想

关键概念：四边界控制

通过维护四个边界来控制遍历范围：

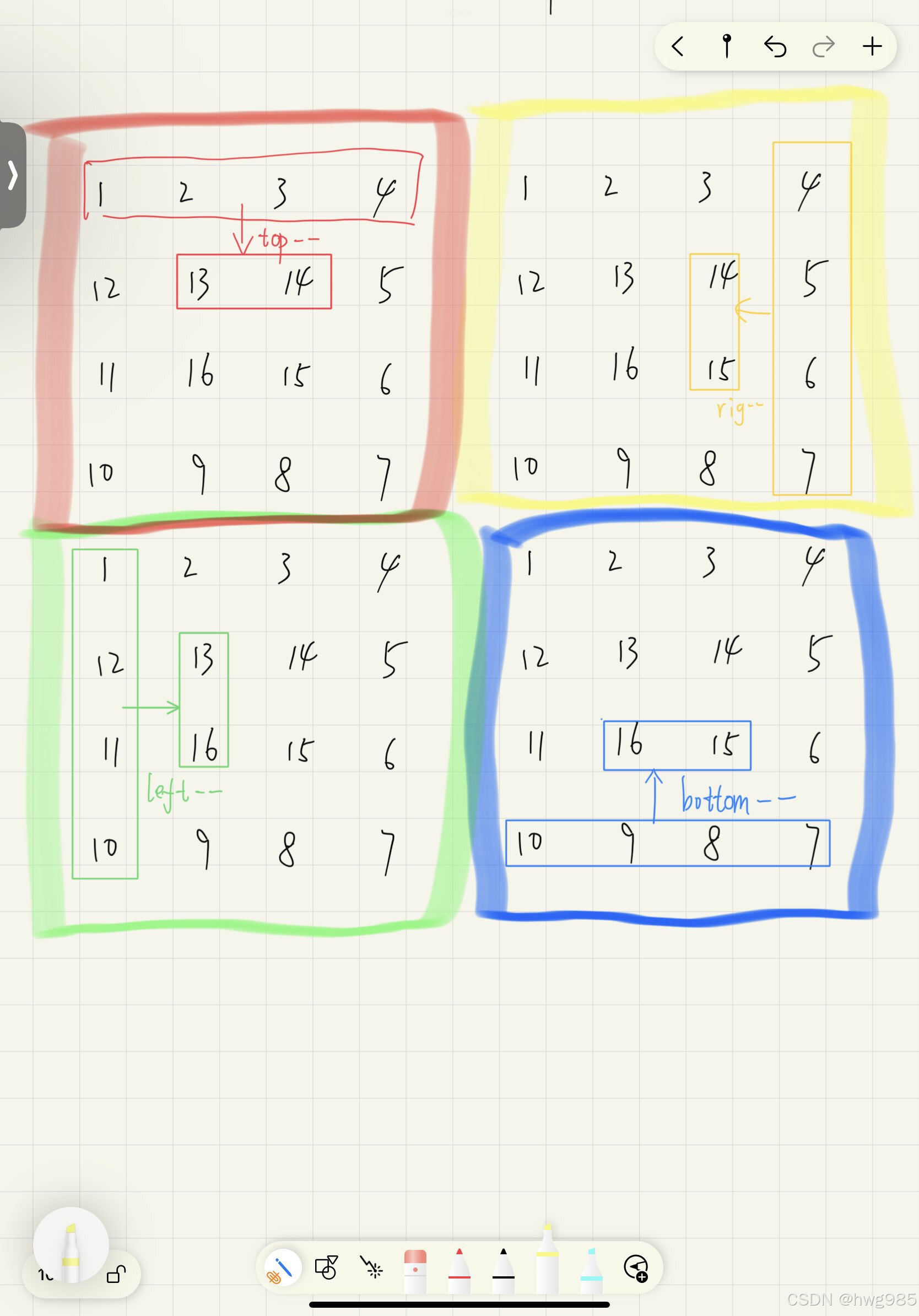
• top：上边界
• bottom：下边界
• left：左边界
• right：右边界

遍历顺序

按照顺时针方向，循环执行四个步骤：

1. 从左到右 遍历上边界
2. 从上到下 遍历右边界
3. 从右到左 遍历下边界
4. 从下到上 遍历左边界

每完成一个方向的遍历，就收缩对应的边界。

算法实现

public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix.length == 0) return result;// 定义四个边界int top = 0;                    // 上边界int bottom = matrix.length - 1; // 下边界  int left = 0;                   // 左边界int right = matrix[0].length - 1; // 右边界while (top <= bottom && left <= right) {// 1. 从左到右遍历上边界for (int col = left; col <= right; col++) {result.add(matrix[top][col]);}top++; // 上边界下移// 2. 从上到下遍历右边界for (int row = top; row <= bottom; row++) {result.add(matrix[row][right]);}right--; // 右边界左移// 3. 从右到左遍历下边界（需要检查是否还有行）if (top <= bottom) {for (int col = right; col >= left; col--) {result.add(matrix[bottom][col]);}bottom--; // 下边界上移}// 4. 从下到上遍历左边界（需要检查是否还有列）if (left <= right) {for (int row = bottom; row >= top; row--) {result.add(matrix[row][left]);}left++; // 左边界右移}}return result;
}

算法步骤详解

示例：3x3矩阵 [[1,2,3],[4,5,6],[7,8,9]]

步骤	操作	遍历元素	边界变化	边界状态
初始	-	-	-	top=0, bottom=2, left=0, right=2
1	左→右(上边界)	1,2,3	top++	top=1, bottom=2, left=0, right=2
2	上→下(右边界)	6,9	right–	top=1, bottom=2, left=0, right=1
3	右→左(下边界)	8,7	bottom–	top=1, bottom=1, left=0, right=1
4	下→上(左边界)	4	left++	top=1, bottom=1, left=1, right=1
5	左→右(上边界)	5	top++	top=2, bottom=1, left=1, right=1
结束	top > bottom	-	-	循环结束

最终结果：[1,2,3,6,9,8,7,4,5]

边界处理的关键点

1. 为什么步骤3和4需要额外判断？

// 步骤3：从右到左遍历下边界
if (top <= bottom) {  // 检查是否还有行for (int col = right; col >= left; col--) {result.add(matrix[bottom][col]);}bottom--;
}// 步骤4：从下到上遍历左边界  
if (left <= right) {  // 检查是否还有列for (int row = bottom; row >= top; row--) {result.add(matrix[row][left]);}left++;
}

原因：避免重复遍历

2. 边界情况分析

单行矩阵：[[1,2,3,4,5]]

步骤1：1,2,3,4,5 (left→right)
步骤2：无元素 (top=1, bottom=0, 不满足top<=bottom)
结果：[1,2,3,4,5] ✅

单列矩阵：[[1],[2],[3]]

步骤1：1 (left→right)
步骤2：2,3 (top→bottom)  
步骤3：跳过 (top>bottom)
步骤4：跳过 (left>right)
结果：[1,2,3] ✅

2x2矩阵：[[1,2],[3,4]]

步骤1：1,2 (top=0→1)
步骤2：4 (right=1→0)
步骤3：3 (bottom=1→0, 满足top<=bottom)
步骤4：跳过 (left>right)
结果：[1,2,4,3] ✅

可视化理解

边界收缩过程

初始状态：
top=0    ┌─────────┐
left=0 → │ 1  2  3 │ ← right=2│ 4  5  6 ││ 7  8  9 │└─────────┘bottom=2第1步后：
top=1    ┌─────────┐
left=0 → │ █  █  █ ││ 4  5  6 │ ← right=2│ 7  8  9 │└─────────┘bottom=2第2步后：
top=1    ┌─────────┐
left=0 → │ █  █  █ ││ 4  5  █ │ ← right=1│ 7  8  █ │└─────────┘bottom=2第3步后：
top=1    ┌─────────┐
left=0 → │ █  █  █ ││ 4  5  █ │ ← right=1│ █  █  █ │└─────────┘bottom=1第4步后：
top=1    ┌─────────┐
left=1 → │ █  █  █ ││ █  5  █ │ ← right=1│ █  █  █ │└─────────┘bottom=1

复杂度分析

• 时间复杂度：O(m×n)
  • 每个元素恰好被访问一次
• 空间复杂度：O(1)
  • 只使用了常数个变量，不考虑结果数组

常见错误

1. 忘记边界检查

// 错误：可能重复遍历
for (int col = right; col >= left; col--) {result.add(matrix[bottom][col]);
}// 正确：需要检查
if (top <= bottom) {for (int col = right; col >= left; col--) {result.add(matrix[bottom][col]);}
}

2. 边界更新顺序错误

// 错误：先更新边界再遍历
top++;
for (int col = left; col <= right; col++) {result.add(matrix[top][col]);
}// 正确：先遍历再更新边界
for (int col = left; col <= right; col++) {result.add(matrix[top][col]);
}
top++;

总结

螺旋矩阵算法的核心是：

1. 四边界控制：top、bottom、left、right
2. 顺时针遍历：右→下→左→上
3. 边界收缩：每完成一个方向就收缩对应边界
4. 重复检查：避免在单行/单列情况下重复遍历

这是一个非常经典的模拟算法，考察边界处理和循环控制能力！