机器学习入门，从线性规划开始

作为工程开发出身的我，之前被几个数学概念迷惑了很久，再讲具体代码之前，先抛几个概念及计算说明方便大家理解

专业术语

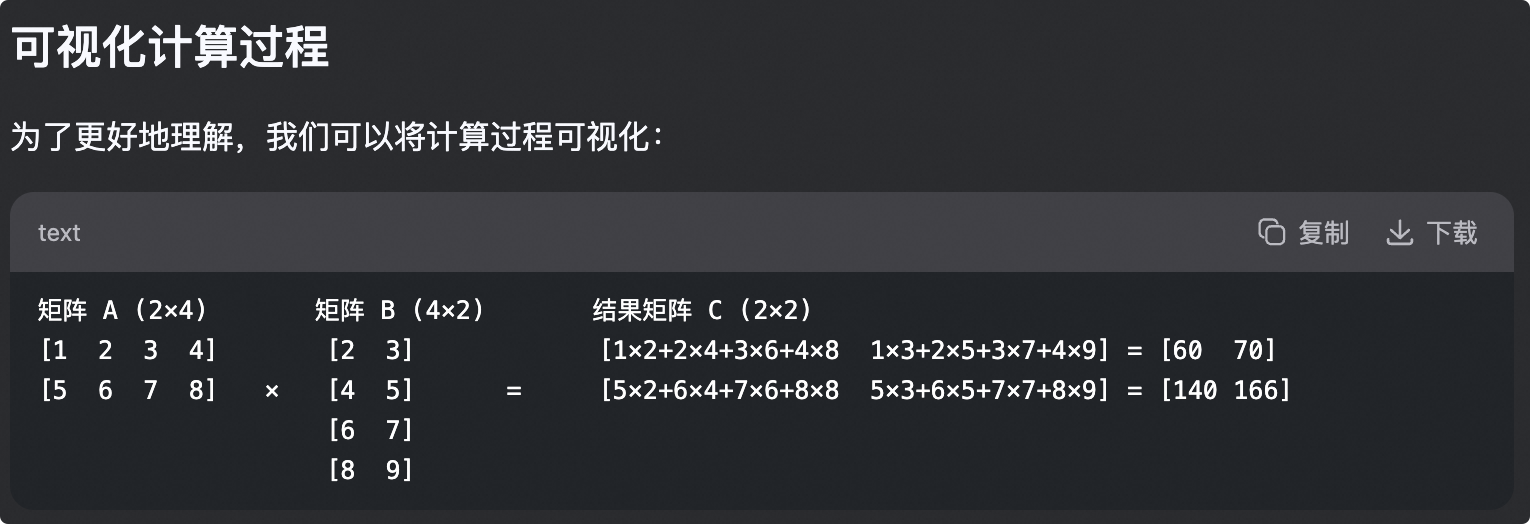
点积

点积计算的结果是一个新的矩阵 ，其中每个元素的计算公式为：
Cᵢⱼ = Σₖ₌₁⁴ Aᵢₖ × Bₖⱼ

2行4列与4行1列的点积示例

2行4列与4行2列的点积示例

偏置项

什么是偏置项？

偏置项（Bias Term）是线性模型中的一个常数项，它代表了当所有输入特征都为0时的预测值。在线性回归中，它通常表示为模型方程中的截距。

数学表示

没有偏置项的线性模型：y = w₁x₁ + w₂x₂ + … + wₙxₙ
有偏置项的线性模型：y = w₀ + w₁x₁ + w₂x₂ + … + wₙxₙ
其中：
● w₀ 是偏置项（截距）
● w₁, w₂, …, wₙ 是特征权重

代码中的实现

def add_bias_term(X):"""在特征矩阵前添加一列1作为偏置项"""return np.c_[np.ones((X.shape[0], 1)), X]

这个函数的作用是：

1. 创建一个全为1的列向量，长度与样本数相同
2. 将这个列向量添加到特征矩阵的前面
3. 这样，矩阵乘法中的第一个权重就会与这个全1列相乘，成为偏置项

示例说明

假设原始特征矩阵为：

X = [[2],  # 样本1的特征[4],  # 样本2的特征[6]]  # 样本3的特征

添加偏置项后：

X_b = [[1, 2],  # 样本1: 偏置项=1, 特征=2[1, 4],  # 样本2: 偏置项=1, 特征=4[1, 6]]  # 样本3: 偏置项=1, 特征=6

对，你没有看错，实际代码实现只是将原来的31矩阵变成了32矩阵，此处的X代表样本集，其中每一个值代表一个特征值，添加偏置项后其实就是为每一个特征值前面增加了一个偏置项，偏置项的值是固定值1

梯度下降

为了帮助您理解梯度下降的工作原理，我将通过一个具体的数值示例来详细解释为什么通过计算梯度和更新参数可以使模型逐渐收敛到最优解。

简单线性回归示例

让我们考虑一个最简单的线性回归问题：只有一个特征，没有偏置项（为了简化）。真实模型为：$y=2x$

1. 生成示例数据

2. 定义模型和损失函数
   我们的模型是：\hat{y} = \theta x损失函数（均方误差）：
   

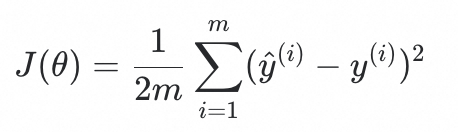
3. 梯度下降过程可视化
   让我们手动执行几次梯度下降迭代，观察参数如何变化：

4. 详细计算过程
   让我们一步步计算第一次迭代：
   

5. 完整迭代过程（下方有完整代码及运行结果）
   让我们继续几次迭代，观察参数如何接近真实值 (θ=2)：

6. 数学原理解释
   为什么梯度下降有效？关键在于梯度指向函数值增长最快的方向，因此负梯度指向函数值下降最快的方向。
   对于我们的损失函数 J(\theta)：
   计算梯度 \frac{\partial J}{\partial \theta}，这表示损失函数在当前点的变化率
   如果梯度为负，说明增加 \theta会减少损失
   如果梯度为正，说明减少 \theta会减少损失
   因此，我们总是沿着负梯度方向更新参数：\theta := \theta - \alpha \frac{\partial J}{\partial \theta}
   在我们的例子中：
   初始 \theta = 0.5，梯度为负 (-11.25)
   负梯度方向是正方向，所以增加 \theta
   更新后 \theta = 1.625，更接近真实值 2
   随着迭代进行，梯度绝对值变小，更新步长变小，逐渐收敛

7. 学习率的影响
   学习率 \alpha控制更新步长的大小：
   \alpha太小：收敛速度慢，需要更多迭代
   \alpha太大：可能跳过最优解，甚至发散

完整代码及运行结果如下

import numpy as np# 生成简单数据
np.random.seed(42)
X = np.array([[1], [2], [3], [4]])  # 特征
y = np.array([[2], [4], [6], [8]])  # 目标值 (y = 2x)print("特征 X:")
print(X)
print("目标值 y:")
print(y)def predict(X, theta):"""预测函数"""return X * thetadef compute_loss(X, y, theta):"""计算损失函数"""m = len(y)predictions = predict(X, theta)return (1/(2*m)) * np.sum((predictions - y) ** 2)def compute_gradient(X, y, theta):"""计算梯度"""m = len(y)predictions = predict(X, theta)errors = predictions - yreturn (1/m) * np.sum(X * errors)  # 对于简单线性回归# 初始参数（随机初始化）
theta = 0.5
alpha = 0.1  # 学习率
iterations = 5print(f"初始参数: theta = {theta}")
print(f"初始损失: {compute_loss(X, y, theta):.6f}")
print()# 执行梯度下降
for i in range(iterations):# 计算梯度grad = compute_gradient(X, y, theta)# 更新参数theta_old = thetatheta = theta - alpha * grad# 计算损失loss = compute_loss(X, y, theta)print(f"迭代 {i + 1}:")print(f"  当前参数: theta = {theta_old:.4f}")print(f"  梯度: {grad:.6f}")print(f"  更新后参数: theta = {theta:.4f}")print(f"  损失: {loss:.6f}")print()

特征 X:
[[1][2][3][4]]
目标值 y:
[[2][4][6][8]]
初始参数: theta = 0.5
初始损失: 8.437500迭代 1:当前参数: theta = 0.5000梯度: -11.250000更新后参数: theta = 1.6250损失: 0.527344迭代 2:当前参数: theta = 1.6250梯度: -2.812500更新后参数: theta = 1.9062损失: 0.032959迭代 3:当前参数: theta = 1.9062梯度: -0.703125更新后参数: theta = 1.9766损失: 0.002060迭代 4:当前参数: theta = 1.9766梯度: -0.175781更新后参数: theta = 1.9941损失: 0.000129迭代 5:当前参数: theta = 1.9941梯度: -0.043945更新后参数: theta = 1.9985损失: 0.000008

可以看到经过5次迭代之后，参数值theta=1.9985（theta 初始值 0.5，是一个随机分配的值），几乎接近正确值2

模型性能指标

回归模型中常用的四个重要性能指标。下面我将详细解释每个指标的含义、计算公式以及如何解读这些指标来评估模型的好坏。

均方误差 (MSE - Mean Squared Error)

计算公式
mse = np.mean((y_true - y_pred) ** 2)

数学公式

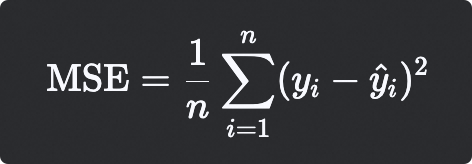
● 解释
MSE衡量的是预测值与真实值之间差异的平方的平均值
● 由于是平方项，MSE会对较大的误差给予更高的惩罚
● 值越小越好，理想值为0

如何判断好坏
● MSE值越小，表示模型的预测精度越高
● 但MSE的值域取决于目标变量的尺度，不同数据集的MSE不能直接比较

均方根误差 (RMSE - Root Mean Squared Error)

计算公式
rmse = np.sqrt(mse)

数学公式

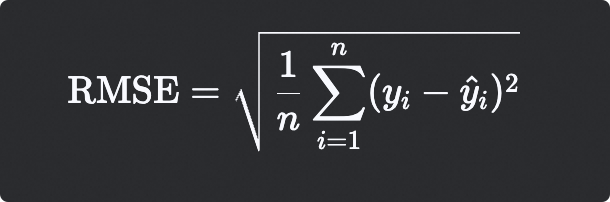
解释

● RMSE是MSE的平方根，与目标变量具有相同的量纲
● 这使得RMSE比MSE更易于解释，因为它与原始数据的单位一致
● 值越小越好，理想值为0

如何判断好坏

● RMSE值越小，表示模型的预测越准确
● 可以直观地理解为"平均预测误差有多大"

平均绝对误差 (MAE - Mean Absolute Error)

计算公式
mae = np.mean(np.abs(y_true - y_pred))

数学公式

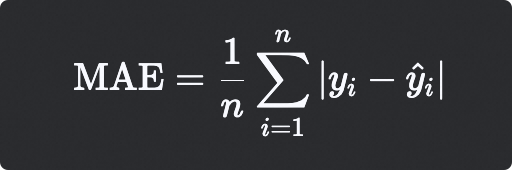
解释
● MAE衡量的是预测值与真实值之间绝对差异的平均值
● 与MSE不同，MAE对所有误差给予相同的权重，不会过分惩罚大误差
● 值越小越好，理想值为0

如何判断好坏
● MAE值越小，表示模型的预测越准确
● 当数据中有异常值时，MAE比MSE/RMSE更稳健

决定系数 (R² - R-Squared)

计算公式

ss_res = np.sum((y_true - y_pred) ** 2)  # 残差平方和
ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)  # 总平方和
r2 = 1 - (ss_res / ss_tot)  # R²

数学公式

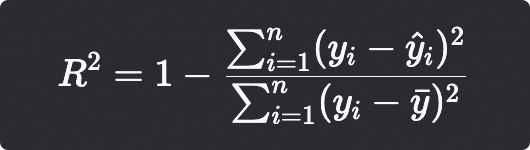
解释
● R²衡量的是模型能够解释的目标变量方差的比例
● 取值范围通常在0到1之间（有时可能为负值）
● 值越接近1越好，理想值为1

如何判断好坏
● R² = 1：模型完美拟合数据
● R² = 0：模型不优于简单使用均值进行预测
● R² < 0：模型表现比简单使用均值还要差
● 一般来说，R² > 0.7 被认为是不错的模型

综合评估模型好坏

● 单一指标评估

○ MSE/RMSE/MAE：值越小越好，但需要考虑目标变量的尺度
○ R²：值越接近1越好，通常认为：■ R² > 0.9：优秀■ 0.7 < R² < 0.9：良好■ 0.5 < R² < 0.7：一般■ R² < 0.5：较差

● 多指标综合评估
在实际应用中，应该综合考虑多个指标：
○ 首先看R²：了解模型解释方差的能力
○ 然后看RMSE/MAE：了解平均预测误差的大小
○ 比较MSE和MAE：
■ 如果MSE远大于MAE，说明存在一些预测误差很大的异常点
■ 如果MSE和MAE接近，说明误差分布相对均匀
● 与其他模型比较
这些指标的绝对值有时难以直接解释，更重要的是：
○ 与基线模型（如均值预测）比较
○ 与不同算法或参数的模型比较
○ 在测试集和验证集上的表现是否一致
● 领域知识考虑
最终判断模型好坏还需要考虑：
○ 业务需求：误差是否在可接受范围内
○ 数据特性：数据的噪声水平和可变性
○ 应用场景：某些应用可能对误差有特殊要求

示例解读
假设您得到以下结果：

MSE: 0.25
RMSE: 0.5
MAE: 0.4
R²: 0.85

您可以这样解读：
● R² = 0.85，说明模型解释了85%的方差，表现良好
● RMSE = 0.5，平均预测误差为0.5个单位
● MAE = 0.4，平均绝对误差为0.4个单位
● MSE(0.25)略大于MAE²(0.16)，说明存在一些稍大的误差，但不算严重

案例实战

在有了前面的数据基础后，我们上一个真实的Case：
已知一个数据集X（这个数据集就是原始样本，可以是M行1列，也可以是M行N列），在这一批数据中经过某个公式运算会得到另外一个数据集Y（M行1列），所谓的机器学习就是利用数据集X推导出一个公式，用于计算出Y来，所谓的公式Y=F(X)就是一个算法模型。

源代码

import numpy as np# 生成示例数据
def generate_sample_data(n_samples=100, noise=0.1):"""生成线性回归示例数据y = 3x + 2 + 噪声"""# 确保可重复性np.random.seed(42)# 生成100行*1列的矩阵X = 2 * np.random.rand(n_samples, 1)# 这里的 noise * np.random.randn(n_samples, 1) 就是噪声y = 3 * X + 2 + noise * np.random.randn(n_samples, 1)return X, y# 添加偏置项到特征矩阵
def add_bias_term(X):"""在特征矩阵前添加一列1作为偏置项"""return np.c_[np.ones((X.shape[0], 1)), X]# 计算带有L2正则化的损失函数
#  函数：compute_loss(X, y, theta, lambda_)
#  输入：
#    X: 特征矩阵，形状为 (m, n)，其中m是样本数量，n是特征数量（包括偏置项，即第一列为1）
#    y: 真实值向量，形状为 (m, 1)
#    theta: 参数向量，形状为 (n, 1)
#    lambda_: 正则化强度
#  输出：
#    损失值（标量）
def compute_loss(X, y, theta, lambda_):"""计算带有L2正则化的均方误差损失"""m = len(y)# predictions就是预测值，为什么 dot运算（dot就是点积运算 dot product）就是预测值呢？# 因为已知是线性回归，所以预测值就是X*theta（X: 特征矩阵，theta: 参数向量）predictions = X.dot(theta)# 均方误差是预测值与真实值之差的平方的平均值。注意这里除以2是为了后续梯度下降求导时方便（平方项求导会产生2，与1/2抵消）。mse = (1 / (2 * m)) * np.sum((predictions - y) ** 2)# L2正则化项是参数向量theta（不包括偏置项，即从第一个参数开始）的平方和乘以正则化强度lambda_除以(2*m)。# 注意：这里不对偏置项（theta[0]）进行正则化，因此使用theta[1:]（即从第一个参数往后）来计算。l2_penalty = (lambda_ / (2 * m)) * np.sum(theta[1:] ** 2)  # 不对偏置项正则化return mse + l2_penalty# 计算梯度
def compute_gradient(X, y, theta, lambda_):"""计算带有L2正则化的梯度"""m = len(y)# predictions就是预测值predictions = X.dot(theta)# 计算预测值与真实值之间的误差：errors = predictions - y# X.T 是X的转置矩阵,比如X是100*2矩阵，那么X.T就是2*100矩阵# errors 比如predictions是100*1矩阵，errors是100*1矩阵# X.T.dot(errors) 其实就是 2*100矩阵 dot 100*1矩阵 = 2*1矩阵# X.T.dot(errors) 运算的基础上乘以 1/m 是为了求平均值gradient = (1 / m) * X.T.dot(errors)# 对非偏置项添加L2正则化梯度gradient[1:] = gradient[1:] + (lambda_ / m) * theta[1:]return gradient# 梯度下降优化
def gradient_descent(X, y, theta, alpha, lambda_, iterations):"""执行带有L2正则化的梯度下降"""m = len(y)loss_history = []for i in range(iterations):# 计算梯度grad = compute_gradient(X, y, theta, lambda_)# 更新参数theta = theta - alpha * grad# 记录损失loss = compute_loss(X, y, theta, lambda_)loss_history.append(loss)# 每100次迭代打印进度if i % 100 == 0:print(f"迭代 {i}: 损失 = {loss:.6f}")return theta, loss_history# 使用模型进行预测
def predict(X, theta):"""使用训练好的模型进行预测"""X_b = add_bias_term(X)return X_b.dot(theta)# 计算模型性能指标
def evaluate_model(y_true, y_pred):"""计算模型性能指标"""mse = np.mean((y_true - y_pred) ** 2)rmse = np.sqrt(mse)mae = np.mean(np.abs(y_true - y_pred))# 计算R²ss_res = np.sum((y_true - y_pred) ** 2)ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)r2 = 1 - (ss_res / ss_tot)return {"MSE": mse,"RMSE": rmse,"MAE": mae,"R²": r2}# 主函数
def main():# 生成数据X, y = generate_sample_data(n_samples=100, noise=0.5)# 添加偏置项X_b = add_bias_term(X)# 初始化参数theta_init = np.random.randn(X_b.shape[1], 1)# 设置超参数alpha = 0.1  # 学习率lambda_ = 1  # 正则化强度iterations = 1000print("初始参数:", theta_init.ravel())print("初始损失:", compute_loss(X_b, y, theta_init, lambda_))print("\n开始训练...")# 训练模型theta_opt, loss_history = gradient_descent(X_b, y, theta_init, alpha, lambda_, iterations)print("\n训练完成!")print("优化后的参数:", theta_opt.ravel())print("优化后的损失:", compute_loss(X_b, y, theta_opt, lambda_))# 进行预测y_pred = predict(X, theta_opt)# 评估模型metrics = evaluate_model(y, y_pred)print("\n模型性能:")for metric, value in metrics.items():print(f"{metric}: {value:.4f}")# 可视化结果try:import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['Hiragino Sans GB']  # 指定默认字体为黑体plt.rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示为方块的问题# 绘制数据和拟合线plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)plt.scatter(X, y, alpha=0.7, label='实际数据')plt.plot(X, y_pred, color='red', label='预测线')plt.xlabel('X')plt.ylabel('y')plt.title('线性回归拟合')plt.legend()plt.grid(True)# 绘制损失下降曲线plt.subplot(1, 2, 2)plt.plot(loss_history)plt.xlabel('迭代次数')plt.ylabel('损失值')plt.title('损失函数下降曲线')plt.grid(True)plt.tight_layout()plt.show()except ImportError:print("未安装matplotlib，跳过可视化部分")return theta_opt, loss_history, metrics# 运行主函数
if __name__ == "__main__":theta_opt, loss_history, metrics = main()

代码解释

生成示例数据
def generate_sample_data(n_samples=100, noise=0.1):添加偏置项到特征矩阵
def add_bias_term(X):计算带有L2正则化的损失函数：
def compute_loss(X, y, theta, lambda_):# 计算梯度
def compute_gradient(X, y, theta, lambda_):# 梯度下降优化（即训练模型，得到优化后的参数theta）
def gradient_descent(X, y, theta, alpha, lambda_, iterations):# 使用模型进行预测
def predict(X, theta):# 计算模型性能指标
def evaluate_model(y_true, y_pred):

运行结果

初始参数: [0.01300189 1.45353408]
初始损失: 6.389668751718595开始训练...
迭代 0: 损失 = 4.085903
迭代 100: 损失 = 0.142653
迭代 200: 损失 = 0.141327
迭代 300: 损失 = 0.141287
迭代 400: 损失 = 0.141286
迭代 500: 损失 = 0.141286
迭代 600: 损失 = 0.141286
迭代 700: 损失 = 0.141286
迭代 800: 损失 = 0.141286
迭代 900: 损失 = 0.141286训练完成!
优化后的参数: [2.18281294 2.80501847]
优化后的损失: 0.14128625685541518模型性能:
MSE: 0.2039
RMSE: 0.4515
MAE: 0.3492
R²: 0.9346

运行结果如下所示，可以看到针对有噪音的一批样本，最终产拟合成y=ax+b的形式，达到预期

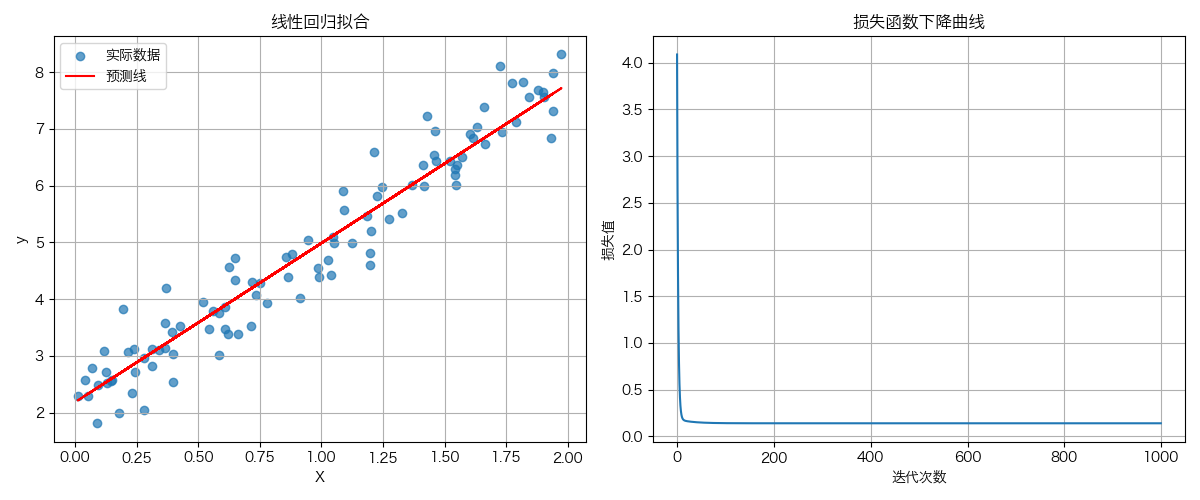
总结

偏置项是线性模型中的一个重要组成部分：

1. 作用：提供模型的基础输出水平，增加模型灵活性
2. 实现：通过在特征矩阵前添加一列1来实现
3. 几何意义：决定拟合线/面的截距
4. 正则化处理：通常不对偏置项进行正则化惩罚