微积分 | 积分代换

注：本文为 “微积分 | 积分代换法 ” 相关合辑。
英文引文，机翻未校，
中文引文，略作重排。
未去重，如有内容异常，请看原文。

---

Integration by Substitution

积分代换法

May 23, 2018 / By Dave Peterson

Last time, we looked at a method of integration, namely partial fractions, so it seems appropriate to find something about another method of integration (this one more specifically part of calculus rather than algebra).
上次，我们研究了一种积分方法，即部分分式积分法，因此现在探讨另一种积分方法（这种方法更属于微积分范畴而非代数）似乎很合适。

We will look at a question about integration by substitution; as a bonus, I will include a list of places to see further examples of substitution.
我们将研究一个关于代换积分法的问题；作为额外的补充，我还会列出一些可以找到更多代换例子的地方。

I have previously written about how and why we can treat differentials ( $dx$ , $dy$ ) as entities distinct from the derivative ( $\frac{dy}{dx}$ ), even though the latter is not really a fraction as it appears to be.
我之前曾写过关于如何以及为何可以将微分（$dx$、$dy$）视为与导数（$\frac{dy}{dx}$）不同的实体，尽管后者看起来并不像一个真正的分数。

One of the pages I referred to there deals more specifically with the idea of integration by substitution, and deserves special attention.
我提到的其中一个页面更具体地讨论了代换积分法的概念，值得特别关注。

What do differentials mean here?

微分在这里是什么意思？

Reuben asked, in 2006,
鲁本在 2006 年问道：

Why Does Integration by Substitution Work?
为什么代换积分法有效？
 
I just learned the process of integration by substitution. My textbook seems to explain it for the most part, but it says “imagine that you multiply $\frac{du}{dx}$ by the $dx$ in the derivative to get $du$ .” This seems to work, but I’ve found online that technically, you can’t treat differentials as numbers that can be “canceled out.”
我刚刚学了代换积分法。我的课本似乎在很大程度上解释了这个方法，但它说“想象一下，你将 $\frac{du}{dx}$ 乘以导数中的 $dx$ 以得到 $du$。”这看起来似乎可行，但我在网上发现，从技术上讲，你不能把微分当作可以“约掉”的数字。
 
A) Is this true? It seems to me that they’re just very very very small numbers. So why could you not cancel them out?
A) 这是真的吗？在我看来，它们只是非常非常非常小的数字。那为什么不能把它们约掉呢？
 
B) If that’s the case, how do you prove that substitution works and use integration by substitution WITHOUT treating differentials as numbers?
B) 如果是这样的话，你如何证明代换是有效的，并且在不把微分当作数字的情况下使用代换积分法呢？

The main question here is, why does treating them that way work here? Can we prove it, rather than just waving our hands and doing magic?
这里的主要问题是，为什么那样处理它们在这里会奏效？我们能否证明这一点，而不是仅仅靠挥挥手施展魔法？

Doctor Fenton first pointed out that the differentials can be thought of just as a way to organize our work, without having to think of them as real things:
芬顿博士首先指出，微分可以仅仅被看作是一种组织我们工作的方式，而无需将它们视为真实存在的东西：

Thanks for writing to Dr. Math. There are several ways to look at differentials, but probably the simplest is to view them as a formal bookkeeping device for keeping track of the constants when finding antiderivatives.
感谢你写信给数学博士。看待微分有几种方式，但可能最简单的是将它们视为一种形式化的簿记工具，用于在寻找原函数时跟踪常数。

This bypasses the question of what they really are, which is not needed for substitution; they are mere notation.
这避开了关于它们真正是什么的问题，而这个问题对于代换来说并不需要；它们只是符号而已。

Then he explained the basic concept of substitution as the counterpart of the chain rule in differentiation:
然后他解释了代换作为微分中链式法则的对应物的基本概念：

Many of the integration (or antidifferentiation) rules are actually counterparts of corresponding differentiation rules, and this is true of the substitution theorem, which is the integral version of the Chain Rule.
许多积分（或求原函数）规则实际上是相应微分规则的对应物，代换定理就是链式法则的积分版本，这一点也不例外。
 
The Chain Rule says that if we have a composite function $F(g(x))$, and if $f(x)=F^{\prime }(x)$ is the derivative of the outer function $F(x)$, then
链式法则指出，如果我们有一个复合函数 $F(g(x))$，并且如果 $f(x)=F^{\prime }(x)$ 是外函数 $F(x)$ 的导数，那么

$$[F(g(x)){]}^{\prime }=F^{\prime }(g(x))\cdot g^{\prime }(x)=f(g(x))\cdot g^{\prime }(x)$$

The antiderivative version of this says that if we want to find the antiderivative of $f(g(x))$ and we know the antiderivative $F$ of $f$, then the antiderivative of $f(g(x))$ is just $F(g(x))$, and we have reduced the problem of finding the antiderivative of the complicated expression $f(g(x))$ to that of finding the antiderivative of $f$, which we usually write with a different independent variable such as $u$.
这个法则的原函数版本指出，如果我们想要求 $f(g(x))$ 的原函数，并且我们知道 $f$ 的原函数 $F$，那么 $f(g(x))$ 的原函数就是 $F(g(x))$，我们已经将求复杂表达式 $f(g(x))$ 的原函数的问题简化为求 $f$ 的原函数的问题，而我们通常会用另一个独立变量，比如 $u$，来表示它。

That is, the Chain Rule says that
也就是说，链式法则表明

$$[F(g(x)){]}^{\prime }=f(g(x))\cdot g^{\prime }(x)\text{(remember that F′=f)}$$

so
所以

$$\int f(g(x))\cdot g^{\prime }(x)dx=F(g(x))+C$$

On the other hand, our definition of $F$ implies that it is an antiderivative (indefinite integral) of $f$, which lets us rewrite the result:
另一方面，我们对 $F$ 的定义表明，它是 $f$ 的一个原函数（不定积分），这使我们可以重新写出结果：

But since $F^{\prime }=f$,
但由于 $F^{\prime }=f$，

$$\int f(u)du=F(u)$$

(the letter used for the variable of integration is a dummy variable, so we can use any letter we wish). This lets us write
（积分变量的字母是一个虚设变量，因此我们可以使用任何我们想要的字母。）这使我们可以写出

$$\int f(g(x))\cdot g^{\prime }(x)dx=\int f(u)du$$

where we understand the right side to be $F(u)$ with $u$ replaced by the formula $g(x)$. So it appears that in the integral on the left side, we replaced $g(x)$ by $u$ and $g^{\prime }(x)dx$ by $du$ (similar to the way it “appears” that the sun rises and sets).
我们理解右边是将 $u$ 替换为公式 $g(x)$ 后的 $F(u)$。因此，在左边的积分中，我们似乎用 $u$ 替换了 $g(x)$，用 $du$ 替换了 $g^{\prime }(x)dx$（类似于“看起来”太阳升起和落下这种方式）。
 
This process doesn’t have to be considered meaningful in itself, but rather just a mnemonic or aid in determining the outer function $f(x)$ in the composition.
这个过程本身不需要被认为是有意义的，而只是一个助记符或帮助确定复合函数中外函数 $f(x)$ 的工具。
 
The differential part of this substitution can also be thought of as a mnemonic, since we can mix Leibnitz and function notation to write, if $u=g(x)$, that
由于我们可以混合使用莱布尼茨和函数符号来表示，如果 $u=g(x)$，那么这个代换的微分部分也可以被认为是一个助记符，

$$\frac{du}{dx}=g^{\prime }(x)$$

and “multiplying” by $dx$ gives $du=g^{\prime }(x)dx$. One can make this procedure logically rigorous by introducing the concept of differential forms, but that requires a lot of mathematical machinery, so that it is easier to just think of it as a formal computation.
并且“乘以” $dx$ 得到 $du=g^{\prime }(x)dx$。通过引入微分形式的概念，可以使这个过程在逻辑上更加严谨，但这需要大量的数学工具，因此更简单的方法是将其视为一种形式化的计算。
 
(There are books such as Bressoud’s Second Year Calculus, Edwards’ Advanced Calculus: A Differential Forms Approach, and Spivak’s Calculus on Manifolds which go over this in detail.)
（有一些书籍，如 Bressoud 的《第二年微积分》、Edwards 的《高级微积分：微分形式方法》和 Spivak 的《流形上的微积分》，详细地讨论了这个问题。）

An example of the process

一个过程的例子

Doctor Fenton then gave an example, showing first how we can recognize a complicated integral as having the form $\int f(g(x))\cdot g^{\prime }(x)dx$, and then how to do it with less insight, just making the substitution and letting the process fill in the details:
芬顿博士接着举了一个例子，首先展示了我们如何识别一个复杂的积分具有 $\int f(g(x))\cdot g^{\prime }(x)dx$ 的形式，然后展示了如何在没有太多洞察力的情况下进行操作，只需进行代换并让过程填补细节：

For example, to integrate
例如，要计算

$$\int [x^3+1{]}^{1/2}{x}^{2}dx$$

we can notice that the integrand has the form of the derivative of a composite function $f(g(x))\cdot g^{\prime }(x)$, with $f(x)=x^{1/2}$ and $g(x)=x^3+1$, but $g^{\prime }(x)=3x^2$, not just $x^2$, so the constant is not quite right.
我们可以注意到，被积函数具有复合函数 $f(g(x))\cdot g^{\prime }(x)$ 的导数形式，其中 $f(x)=x^{1/2}$，$g(x)=x^3+1$，但 $g^{\prime }(x)=3x^2$，而不是仅仅 $x^2$，因此常数并不完全正确。
 
However, if we multiply and divide by 3, we have
然而，如果我们乘以并除以 3，我们得到

$$\int [x^3+1{]}^{1/2}{x}^{2}dx=\frac{1}{3}\int [x^3+1{]}^{1/2}\cdot (3x^2)dx$$

and the integrand on the right is exactly a derivative now, of the composite function $\frac{2}{3}[x^3+1{]}^{3/2}$ (we can see this because the outer function $f(x)$ is $x^{1/2}$, whose antiderivative $F(x)$ is $\frac{2}{3}{x}^{3/2}$, so the antiderivative is $\frac{1}{3}F(g(x))$).
右边的被积函数现在正好是一个复合函数 $\frac{2}{3}[x^3+1{]}^{3/2}$ 的导数（我们可以看到这一点，因为外函数 $f(x)$ 是 $x^{1/2}$，其原函数 $F(x)$ 是 $\frac{2}{3}{x}^{3/2}$，因此原函数是 $\frac{1}{3}F(g(x))$）。
 
This argument has computed the integral or antiderivative without substitution.
这个论证在没有使用代换的情况下计算了积分或原函数。

To use substitution, we let $u=x^3+1$, and $du=3x^{2}dx$, so that $x^{2}dx=\frac{1}{3}du$, and
要使用代换，我们设 $u=x^3+1$，且 $du=3x^{2}dx$，因此 $x^{2}dx=\frac{1}{3}du$，于是

$$\begin{array}{rl}\int [x^3+1{]}^{1/2}{x}^{2}dx& =\int u^{1/2}\cdot \frac{1}{3}du\\ & =\frac{1}{3}\cdot \frac{2}{3}{u}^{3/2}+C\\ & =\frac{2}{9}[x^3+1{]}^{3/2}+C\end{array}$$

Substitution makes the process fairly mechanical so it doesn’t require much thought, once you see the appropriate substitution to use, and it also automatically keeps the constants straight.
代换使这个过程相当机械化，因此一旦你看到了合适的代换方法，就不需要太多思考，并且它还能自动地保持常数的正确性。

The important thing in integration is the end result:
积分中重要的是最终结果：

The objective of indefinite integration is to find an antiderivative, and exactly how you do that isn’t really important, at least in my opinion. If you can just look at a formula and “see” what the antiderivative is, you have solved the problem.
不定积分的目标是找到一个原函数，而你具体如何做到这一点并不真的重要，至少在我看来是这样。如果你能够仅仅通过查看一个公式就能“看出”原函数是什么，那么你就已经解决了问题。
 
Most of us can’t do that, and there are a number of procedures to help, such as the substitution rule, and integration by parts (the integral version of the Product Rule of differentiation).
大多数人做不到这一点，因此有一些程序可以帮助，比如代换规则和分部积分法（微分乘积法则的积分版本）。
 
The real theory behind substitution is the Chain Rule, and you can look at the details of substitution as a formal process for helping you see the important parts of the composite functions involved, without worrying about their intrinsic meaning.
代换背后的真正理论是链式法则，你可以将代换的细节视为一种形式化的程序，帮助你看到所涉及的复合函数的重要部分，而无需担心它们的内在含义。

More examples of substitution

更多代换的例子

One example doesn’t cover all the subtleties in using the method, so let’s look at more.
一个例子并不能涵盖使用这种方法的所有细微之处，因此我们再来看一些。

The following pages, arranged from straightforward to relatively complicated, show various Math Doctors’ different styles of substitution, and contexts in which it can be applied:
以下页面按从简单到相对复杂排列，展示了不同数学博士的代换风格以及可以应用的上下文：

• Integrate Cos $2a$
  对 Cos2a 积分

  [ $\int \cos (ax)dx$ , Doctor Peterson]

• Integral using Substitution
  代换积分

  [ $\int \frac{x}{\sqrt{x^2+1}}dx$ , Doctor Sydney]

• Integration
  求积分

  [ $\int (2-x^2{)}^{4}xdx$ , Doctor Jerry]

• A Change of Variables
  变量的变化

  [ $\int (\sin (2x){)}^5\cdot \cos (2x)dx$ , Doctor Luis]

• Substituting to Simplify the Integral
  代入化简积分

  [ $\int {\tan }^3(x)\sec xdx$ , Doctor Barrus]

• Integration of Trigonometric Function by Substitution
  三角函数的代换积分

  [ $\int \tan (2x)dx$ , Doctor Sam]

• A Trigonometry Integral Requiring Two Substitutions
  一个需要两次替换的三角积分

  [ $\int \sqrt{1+\sin (x)}dx$ , Doctor Sam]

In most of these, as usual, we just took the student through the hard part and let him finish. A couple, from early in the history of Ask Dr. Math, go all the way to the answer, where that seemed appropriate. But all demonstrate how to think through the details.
在大多数情况下，和往常一样，我们只是引导学生攻克了难题的核心部分，剩下的则让他们自行完成。其中有两例来自 “数学博士问答”（Ask Dr. Math）早期的案例，考虑到实际情况适宜，我们会全程引导至最终答案。但所有案例都体现了如何逐步梳理细节、推导思路的方法。

---

高等数学 第五章 定积分（4）定积分的换元法

gukedream 于 2019-01-08 21:31:58 发布

§5.4 定积分的换元法

一、换元公式

【定理】

若满足以下三个条件：

1. 函数 $f(x)$ 在区间 $[a,b]$ 上连续；
2. 函数 $x=\phi (t)$ 在区间 $[\alpha ,\beta ]$（或 $[\beta ,\alpha ]$）上单值，且具有连续导数；
3. 当 $t$ 在 $[\alpha ,\beta ]$（或 $[\beta ,\alpha ]$）上变化时，$x=\phi (t)$ 的值在 $[a,b]$ 上变化，且 $\phi (\alpha )=a$，$\phi (\beta )=b$；

则有定积分换元公式：
$${\int }_a^{b}f(x)\mathrm{d}x={\int }_{\alpha }^{\beta }f\left[\phi (t)\right]{\phi }^{\prime }(t)\mathrm{d}t\text{\hspace{1em}(1)}$$

【证明】

由于式（1）中两端的被积函数均在其对应积分区间上连续，因此两端的定积分均存在，且两端被积函数的原函数也均存在。

设 $F(x)$ 是 $f(x)$ 在 $[a,b]$ 上的一个原函数，根据牛顿 - 莱布尼兹公式，有：
$${\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a)$$

另一方面，考虑函数 $F\left[\phi (t)\right]$ 对 $t$ 的导数，由复合函数求导法则可得：
$$\frac{\mathrm{d}}{\mathrm{d}t}F\left[\phi (t)\right]=F^{\prime }\left[\phi (t)\right]\cdot {\phi }^{\prime }(t)=f\left[\phi (t)\right]\cdot {\phi }^{\prime }(t)$$

这表明 $F\left[\phi (t)\right]$ 是 $f\left[\phi (t)\right]{\phi }^{\prime }(t)$ 在 $[\alpha ,\beta ]$（或 $[\beta ,\alpha ]$）上的一个原函数。再根据牛顿 - 莱布尼兹公式，有：
$${\int }_{\alpha }^{\beta }f\left[\phi (t)\right]{\phi }^{\prime }(t)\mathrm{d}t=F\left[\phi (\beta )\right]-F\left[\phi (\alpha )\right]$$

又因为 $\phi (\alpha )=a$，$\phi (\beta )=b$，所以：
$$F\left[\phi (\beta )\right]-F\left[\phi (\alpha )\right]=F(b)-F(a)$$

综上，可得：
$${\int }_a^{b}f(x)\mathrm{d}x={\int }_{\alpha }^{\beta }f\left[\phi (t)\right]{\phi }^{\prime }(t)\mathrm{d}t$$

【对定理的注解】

1. 采用变量替换 $x=\phi (t)$ 将原变量 $x$ 代换为新变量 $t$ 时，原定积分的积分限必须同步替换为新变量 $t$ 的积分限；求出 $f\left[\phi (t)\right]{\phi }^{\prime }(t)$ 的原函数 $F\left[\phi (t)\right]$ 后，无需像不定积分那样将其还原为原变量 $x$ 的函数，只需将新变量 $t$ 的上下限代入原函数并计算差值即可。

2. 应用变量替换时需严格遵循换元条件，避免计算错误，具体条件如下：

   • 变换函数 $x=\phi (t)$ 在对应区间上单值，且其导数 ${\phi }^{\prime }(t)$ 连续；
   • 变换函数满足 $\phi (\alpha )=a$，$\phi (\beta )=b$。

3. 当 $\alpha >\beta$ 时，定积分换元公式（1）仍然成立。

例题 1 求 ${\int }_1^4\frac{dx}{1+\sqrt{x}}$

解法一

令 $\sqrt{x}=t$

当 $x=1$ 时，$t=1$；当 $x=4$ 时，$t=2$。

又当 $t\in [1,2]$ 时，有 $x=t^2\in [1,4]$，且变换函数 $x=t^2$ 在 $[1,2]$ 上单值，$\frac{dx}{dt}=2t$ 在 $[1,2]$ 上连续，

由换元公式有

$$\begin{array}{rl}{\int }_1^4\frac{dx}{1+\sqrt{x}}& ={\int }_1^2\frac{2tdt}{1+t}\\ & =2{\int }_1^2\left[1-\frac{1}{1+t}\right]dt\\ & =2{\left[t-\ln (1+t)\right]}_1^2\\ & =2(1-\ln 3+\ln 2)\end{array}$$

解法二

令 $-\sqrt{x}=t$

当 $x=1$ 时，$t=-1$；当 $x=4$ 时，$t=-2$。

又当 $t\in [-2,-1]$ 时，$x=t^2\in [1,4]$，且变换函数 $x=t^2$ 在 $[-2,-1]$ 上单值，$\frac{dx}{dt}=2t$ 在 $[-2,-1]$ 上连续，

由换元公式有

$$\begin{array}{rl}{\int }_1^4\frac{dx}{1+\sqrt{x}}& ={\int }_{-2}^{-1}\frac{2tdt}{1-t}\\ & =2{\int }_{-1}^{-2}\left[\frac{1}{1-t}-1\right]dt\\ & =2{\left[-\ln (1-t)-t\right]}_{-1}^{-2}\\ & =2(-\ln 3+2+\ln 2-1)\\ & =2(1-\ln 3+\ln 2)\end{array}$$

注意：
在 解法二 中，经过换元，定积分的下限较上限大。

换元公式也可以反过来，即
$${\int }_a^{b}f(\phi (x)){\phi }^{\prime }(x)dx\iff {\int }_{\phi (a)}^{\phi (b)}f(t)dt(a=\phi (\alpha ),b=\phi (\beta ))$$

【例 2】计算定积分 ${\int }_0^{\frac{\pi }{2}}{\cos }^{5}x\sin xdx$

解：设 $u=\cos x$，则 $\mathrm{d}u=-\sin x\mathrm{d}x$，即 $-\mathrm{d}u=\sin x\mathrm{d}x$。

确定积分限：当 $x=0$ 时，$u=1$；当 $x=\frac{\pi }{2}$ 时，$u=0$。

代入原定积分得：
$$\begin{array}{rl}{\int }_0^{\frac{\pi }{2}}{\cos }^{5}x\sin x\mathrm{d}x& =-{\int }_1^0{u}^5\mathrm{d}u\\ & ={\int }_0^1{u}^5\mathrm{d}u\\ & =\frac{u^6}{6}{|}_0^1\\ & =\frac{1}{6}-0\\ & =\frac{1}{6}\end{array}$$

一般而言，此类换元可不必明确写出新变量（如本例中的 $u$），相应地也无需改变定积分的上下限，直接通过 “凑微分” 计算即可，过程如下：
$$\begin{array}{rl}{\int }_0^{\frac{\pi }{2}}{\cos }^{5}x\sin x\mathrm{d}x& =-{\int }_0^{\frac{\pi }{2}}{\cos }^{5}x\mathrm{d}(\cos x)\\ & =-\frac{{\cos }^{6}x}{6}{|}_0^{\frac{\pi }{2}}\\ & =-\left(0-\frac{1}{6}\right)\\ & =\frac{1}{6}\end{array}$$

二、常用的变量替换技术与几个常用结论

【例 3】证明：若函数 $f(x)$ 在区间 $[-a,a]$ 上连续，则

1. 若 $f(x)$ 为偶函数，则 ${\int }_{-a}^{a}f(x)\mathrm{d}x=2{\int }_0^{a}f(x)\mathrm{d}x$；
2. 若 $f(x)$ 为奇函数，则 ${\int }_{-a}^{a}f(x)\mathrm{d}x=0$。

证明：
根据定积分对积分区间的可加性，将积分拆分为两部分：
$${\int }_{-a}^{a}f(x)\mathrm{d}x={\int }_{-a}^{0}f(x)\mathrm{d}x+{\int }_0^{a}f(x)\mathrm{d}x\text{\hspace{1em}(2)}$$

对式（2）中的 ${\int }_{-a}^{0}f(x)\mathrm{d}x$ 作变量替换：令 $x=-t$，则 $\mathrm{d}x=-\mathrm{d}t$。
确定积分限：当 $x=-a$ 时，$t=a$；当 $x=0$ 时，$t=0$。

代入得：
$$\begin{array}{rl}{\int }_{-a}^{0}f(x)\mathrm{d}x& ={\int }_a^{0}f(-t)\cdot (-\mathrm{d}t)\\ & ={\int }_0^{a}f(-t)\mathrm{d}t\end{array}$$

由于定积分的值与积分变量的符号无关，故 ${\int }_0^{a}f(-t)\mathrm{d}t={\int }_0^{a}f(-x)\mathrm{d}x$，因此：
$${\int }_{-a}^{0}f(x)\mathrm{d}x={\int }_0^{a}f(-x)\mathrm{d}x\text{\hspace{1em}(3)}$$

将式（3）代入式（2），得：
$$\begin{array}{rl}{\int }_{-a}^{a}f(x)\mathrm{d}x& ={\int }_0^{a}f(-x)\mathrm{d}x+{\int }_0^{a}f(x)\mathrm{d}x\\ & ={\int }_0^a\left[f(-x)+f(x)\right]\mathrm{d}x\end{array}\text{\hspace{1em}(4)}$$

1. 若 $f(x)$ 为偶函数，则 $f(-x)=f(x)$，代入式（4）得：
   $$\begin{array}{rl}{\int }_{-a}^{a}f(x)\mathrm{d}x& ={\int }_0^a\left[f(x)+f(x)\right]\mathrm{d}x\\ & =2{\int }_0^{a}f(x)\mathrm{d}x\end{array}$$

2. 若 $f(x)$ 为奇函数，则 $f(-x)=-f(x)$，代入式（4）得：
   $$\begin{array}{rl}{\int }_{-a}^{a}f(x)\mathrm{d}x& ={\int }_0^a\left[-f(x)+f(x)\right]\mathrm{d}x\\ & ={\int }_0^{a}0\mathrm{d}x\\ & =0\end{array}$$

【结论说明】

1. 该结论可用于简化定义在关于原点对称的区间 $[-a,a]$ 上的偶函数与奇函数的定积分计算，避免复杂的积分运算；

2. 计算 ${\int }_{-a}^{a}f(x)\mathrm{d}x$ 时所用的变量替换 $x=-t$ 虽形式简单，但在对称区间积分的简化中应用广泛。

【例 4】若函数 $f(x)$ 在区间 $[0,1]$ 上连续，证明：

1. ${\int }_0^{\frac{\pi }{2}}f(\sin x)\mathrm{d}x={\int }_0^{\frac{\pi }{2}}f(\cos x)\mathrm{d}x$；

2. ${\int }_0^{\pi }xf(\sin x)\mathrm{d}x=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)\mathrm{d}x$。

并利用上述结论计算定积分 ${\int }_0^{\pi }\frac{x\sin x}{1+{\cos }^{2}x}\mathrm{d}x$。

1. 证明 ${\int }_0^{\frac{\pi }{2}}f(\sin x)\mathrm{d}x={\int }_0^{\frac{\pi }{2}}f(\cos x)\mathrm{d}x$：

设 $x=\frac{\pi }{2}-t$，则 $\mathrm{d}x=-\mathrm{d}t$。

确定积分限：当 $x=0$ 时，$t=\frac{\pi }{2}$；当 $x=\frac{\pi }{2}$ 时，$t=0$。

代入原定积分得：
$$\begin{array}{rl}{\int }_0^{\frac{\pi }{2}}f(\sin x)\mathrm{d}x& ={\int }_{\frac{\pi }{2}}^{0}f\left[\sin \left(\frac{\pi }{2}-t\right)\right]\cdot (-\mathrm{d}t)\\ & ={\int }_{\frac{\pi }{2}}^{0}f(\cos t)\cdot (-\mathrm{d}t)\\ & ={\int }_0^{\frac{\pi }{2}}f(\cos t)\mathrm{d}t\end{array}$$

由于定积分与积分变量符号无关，故 ${\int }_0^{\frac{\pi }{2}}f(\cos t)\mathrm{d}t={\int }_0^{\frac{\pi }{2}}f(\cos x)\mathrm{d}x$，因此：
$${\int }_0^{\frac{\pi }{2}}f(\sin x)\mathrm{d}x={\int }_0^{\frac{\pi }{2}}f(\cos x)\mathrm{d}x$$

2. 证明 ${\int }_0^{\pi }xf(\sin x)\mathrm{d}x=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)\mathrm{d}x$：

设 $x=\pi -t$，则 $\mathrm{d}x=-\mathrm{d}t$。

确定积分限：当 $x=0$ 时，$t=\pi$；当 $x=\pi$ 时，$t=0$。

代入原定积分得：
$$\begin{array}{rl}{\int }_0^{\pi }xf(\sin x)\mathrm{d}x& ={\int }_{\pi }^0(\pi -t)f\left[\sin (\pi -t)\right]\cdot (-\mathrm{d}t)\\ & ={\int }_{\pi }^0(\pi -t)f(\sin t)\cdot (-\mathrm{d}t)\\ & ={\int }_0^{\pi }(\pi -t)f(\sin t)\mathrm{d}t\\ & =\pi {\int }_0^{\pi }f(\sin t)\mathrm{d}t-{\int }_0^{\pi }tf(\sin t)\mathrm{d}t\end{array}$$

由于定积分与积分变量符号无关，故

$$\begin{array}{rl}\pi {\int }_0^{\pi }f(\sin t)\text{d}t& =\pi {\int }_0^{\pi }f(\sin x)\text{d}x\\ {\int }_0^{\pi }tf(\sin t)\text{d}t& ={\int }_0^{\pi }xf(\sin x)\text{d}x\end{array}$$

因此：
$${\int }_0^{\pi }xf(\sin x)\mathrm{d}x=\pi {\int }_0^{\pi }f(\sin x)\mathrm{d}x-{\int }_0^{\pi }xf(\sin x)\mathrm{d}x$$

将含 ${\int }_0^{\pi }xf(\sin x)\mathrm{d}x$ 的项移至等式左侧，得：
$$2{\int }_0^{\pi }xf(\sin x)\mathrm{d}x=\pi {\int }_0^{\pi }f(\sin x)\mathrm{d}x$$

两边同时除以 2，即：
$${\int }_0^{\pi }xf(\sin x)\mathrm{d}x=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)\mathrm{d}x$$

利用结论计算 ${\int }_0^{\pi }\frac{x\sin x}{1+{\cos }^{2}x}\mathrm{d}x$：

观察被积函数 $\frac{x\sin x}{1+{\cos }^{2}x}$，可令 $f(\sin x)=\frac{\sin x}{1+{\cos }^{2}x}$，

即 $f(u)=\frac{u}{1+(1-u^2)}$（其中 $u=\sin x$，${\cos }^{2}x=1-{\sin }^{2}x=1-u^2$），满足例 4 中结论 2 的条件。

根据结论 2，有：
$${\int }_0^{\pi }\frac{x\sin x}{1+{\cos }^{2}x}\mathrm{d}x=\frac{\pi }{2}{\int }_0^{\pi }\frac{\sin x}{1+{\cos }^{2}x}\mathrm{d}x$$

计算 ${\int }_0^{\pi }\frac{\sin x}{1+{\cos }^{2}x}\mathrm{d}x$：

设 $u=\cos x$，则 $\mathrm{d}u=-\sin x\mathrm{d}x$，即 $-\mathrm{d}u=\sin x\mathrm{d}x$。

确定积分限：当 $x=0$ 时，$u=1$；当 $x=\pi$ 时，$u=-1$。

代入得：
$$\begin{array}{rl}{\int }_0^{\pi }\frac{\sin x}{1+{\cos }^{2}x}\mathrm{d}x& =-{\int }_1^{-1}\frac{\mathrm{d}u}{1+u^2}\\ & ={\int }_{-1}^1\frac{\mathrm{d}u}{1+u^2}\\ & =\arctan u{|}_{-1}^1\\ & =\arctan 1-\arctan (-1)\\ & =\frac{\pi }{4}-\left(-\frac{\pi }{4}\right)\\ & =\frac{\pi }{2}\end{array}$$

因此：
$${\int }_0^{\pi }\frac{x\sin x}{1+{\cos }^{2}x}\mathrm{d}x=\frac{\pi }{2}\times \frac{\pi }{2}=\frac{{\pi }^2}{4}$$

【结论启示】

1. 计算定积分并非仅能使用牛顿 - 莱布尼兹公式（即先求原函数，再代入上下限计算）；

2. 可通过变量替换的方法直接计算定积分，或利用变量替换简化定积分的计算过程。

   如例 4 中通过替换将复杂积分转化为易计算的形式。

【例 5】计算定积分 ${\int }_0^{\frac{\pi }{2}}\frac{\sin x}{\sin x+\cos x}\mathrm{d}x$

解：设 $I={\int }_0^{\frac{\pi }{2}}\frac{\sin x}{\sin x+\cos x}\mathrm{d}x$。

根据例 4 中结论 1（${\int }_0^{\frac{\pi }{2}}f(\sin x)\mathrm{d}x={\int }_0^{\frac{\pi }{2}}f(\cos x)\mathrm{d}x$），对 $I$ 作变量替换 $x=\frac{\pi }{2}-t$，则 $\mathrm{d}x=-\mathrm{d}t$，当 $x=0$ 时 $t=\frac{\pi }{2}$，当 $x=\frac{\pi }{2}$ 时 $t=0$，代入得：

$$\begin{array}{rl}I& ={\int }_{\frac{\pi }{2}}^0\frac{\sin \left(\frac{\pi }{2}-t\right)}{\sin \left(\frac{\pi }{2}-t\right)+\cos \left(\frac{\pi }{2}-t\right)}\cdot (-\text{d}t)\\ & ={\int }_0^{\frac{\pi }{2}}\frac{\cos t}{\cos t+\sin t}\text{d}t\\ & ={\int }_0^{\frac{\pi }{2}}\frac{\cos x}{\sin x+\cos x}\text{d}x\end{array}$$

将 $I$ 与上式相加，得：
$$I+I={\int }_0^{\frac{\pi }{2}}\frac{\sin x}{\sin x+\cos x}\mathrm{d}x+{\int }_0^{\frac{\pi }{2}}\frac{\cos x}{\sin x+\cos x}\mathrm{d}x$$

即：
$$2I={\int }_0^{\frac{\pi }{2}}\frac{\sin x+\cos x}{\sin x+\cos x}\mathrm{d}x={\int }_0^{\frac{\pi }{2}}\mathrm{d}x=t{|}_0^{\frac{\pi }{2}}=\frac{\pi }{2}$$

两边同时除以 2，得：
$$I=\frac{\pi }{4}$$

故 ${\int }_0^{\frac{\pi }{2}}\frac{\sin x}{\sin x+\cos x}\mathrm{d}x=\frac{\pi }{4}$。

评注：该定积分的计算未通过求被积函数的原函数，仅利用了变量替换与定积分的基本性质（积分区间可加性、积分变量符号无关性），这种 “利用对称性与变量替换简化计算” 的思路具有重要参考价值，值得学习与掌握。

---

高等数学学习笔记——积分的变量替换法

预见未来to50于 2020-01-16 22:41:15 发布

1. 问题引入（牛顿-莱布尼茨公式；基本公式——导数公式与积分公式）

2. 不定积分的第一类换元积分公式（配元法，凑微分法）

3. 不定积分的第二类换元法

4. 定积分的换元公式（口诀：换元先换限；配元不换限）

---

换元积分法

菜瓜变菜鸟于 2020-08-19 12:38:48 发布

一、补充：不定积分的线性运算法则

在正式展开换元积分法之前，首先介绍不定积分的线性运算法则，其表达式如下：

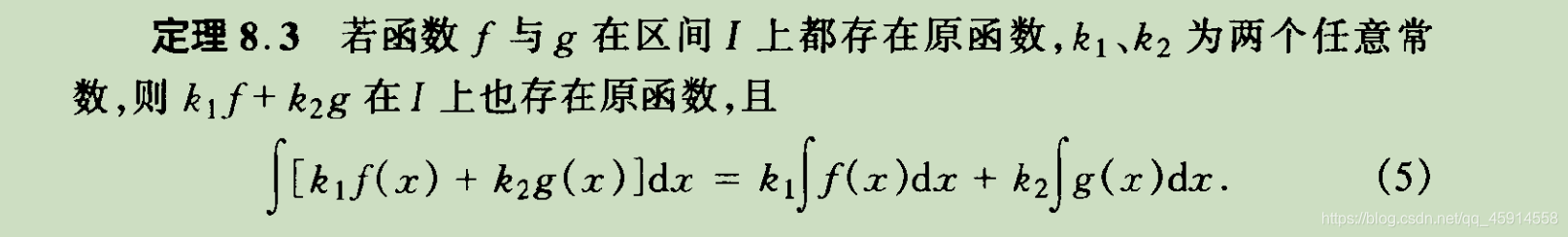
二、换元积分法的定理表达

换元积分法由复合函数求导法则推导得出，其核心定理表达式如下：

上图中公式 (1) 与公式 (2) 分别对应两种逆向的换元逻辑：

• 将公式 (1) 对应的积分还原方式定义为第一换元积分法；

• 将公式 (2) 对应的积分还原方式定义为第二换元积分法。

三、第一换元积分法

3.1 公式表达

第一换元积分法的标准公式形式如下：

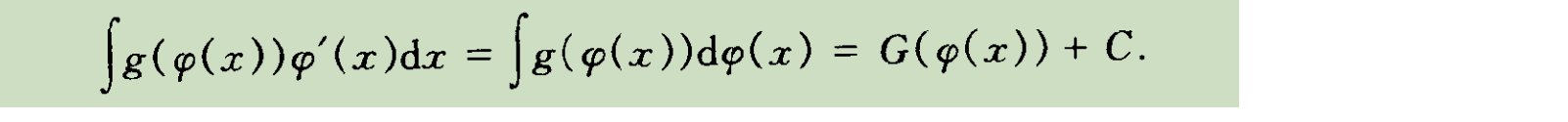
3.2 例题解析

通过具体例题说明第一换元积分法的应用过程：

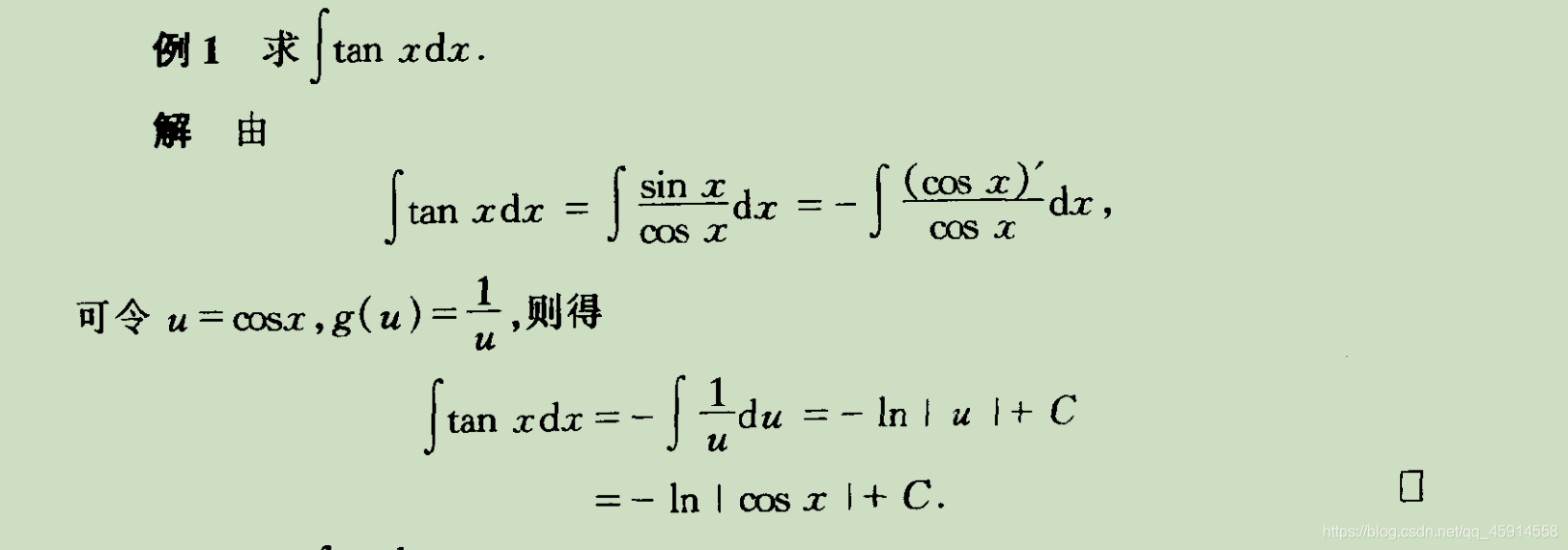
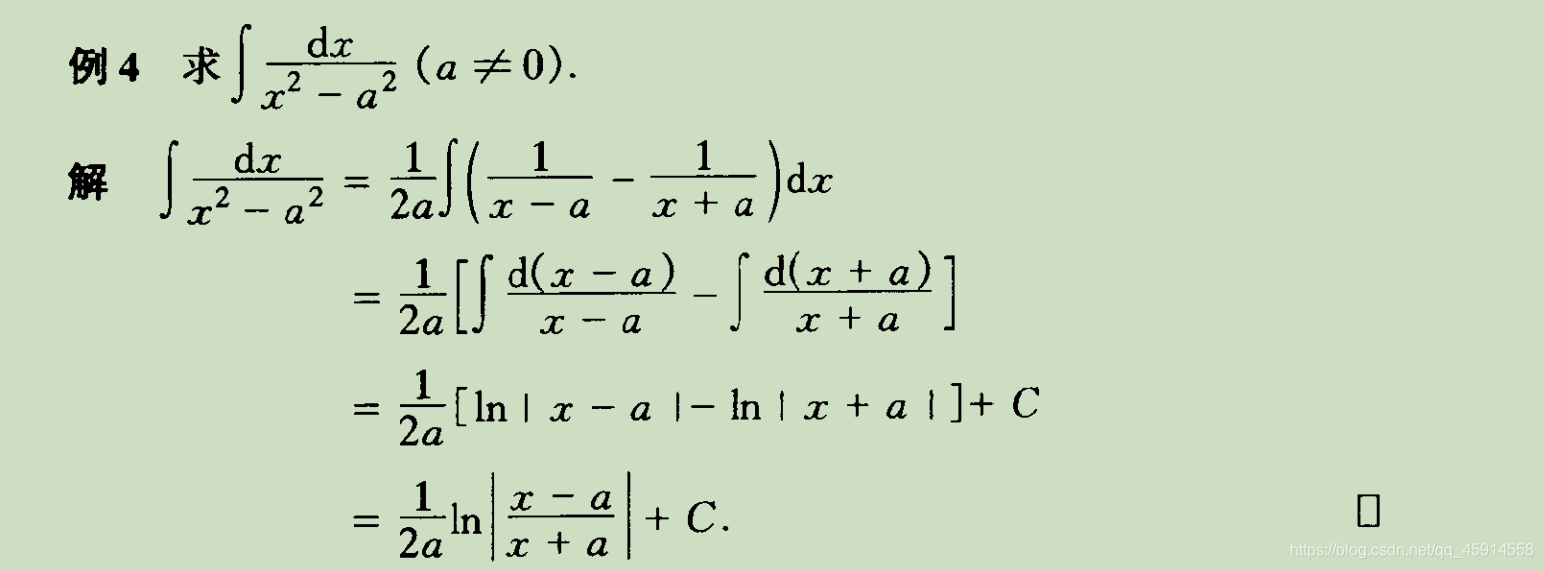
3.3 方法总结

第一换元积分法的核心思路与步骤总结如下：

四、第二换元积分法

4.1 公式与原理

第二换元积分法的核心公式及应用原理如下：

4.2 例题解析

通过具体例题说明第二换元积分法的应用过程：

4.3 两种换元法的交叉应用

部分不定积分问题可同时通过第一换元积分法与第二换元积分法求解，示例如下：

---

via：

• Integration by Substitution
  https://www.themathdoctors.org/integration-by-substitution/

• 高等数学：第五章 定积分（4） 定积分的换元法_定积分换元法-CSDN博客
  https://blog.csdn.net/gukedream/article/details/86100474

• 高等数学学习笔记——第四十一讲——积分的变量替换法_积分变量替换的原则-CSDN博客
  https://blog.csdn.net/hpdlzu80100/article/details/104012117

• 换元积分法详解-CSDN博客
  https://blog.csdn.net/qq_45914558/article/details/108095970

• 第二换元积分法(别称变量代换法) - Preparing - 博客园
  https://www.cnblogs.com/Preparing/p/18190307