【数学·三角函数】两角和差公式 二倍角公式
上一篇:【数学·三角函数】弧度制与诱导公式 (前置知识)
上期习题答案:(1).35(1).\dfrac{3}{5}(1).53;(2).245(2).\dfrac{24}{5}(2).524。
两角和差公式
上期已经讲过诱导公式,但是,对于一些奇怪的角度,比如 sin15∘\sin 15^{\circ}sin15∘,应该怎么求呢?可以想到转化为 sin(45∘−30∘)\sin (45^{\circ}-30^{\circ})sin(45∘−30∘),此处,我们引入两角和差公式 来解决这个问题。
如图,在矩形 ABCDABCDABCD 中,点 EEE 在 BCBCBC 上,连接 AEAEAE 并作 EF⊥AEEF\perp AEEF⊥AE 交 CDCDCD 于点 FFF,连接AFAFAF。
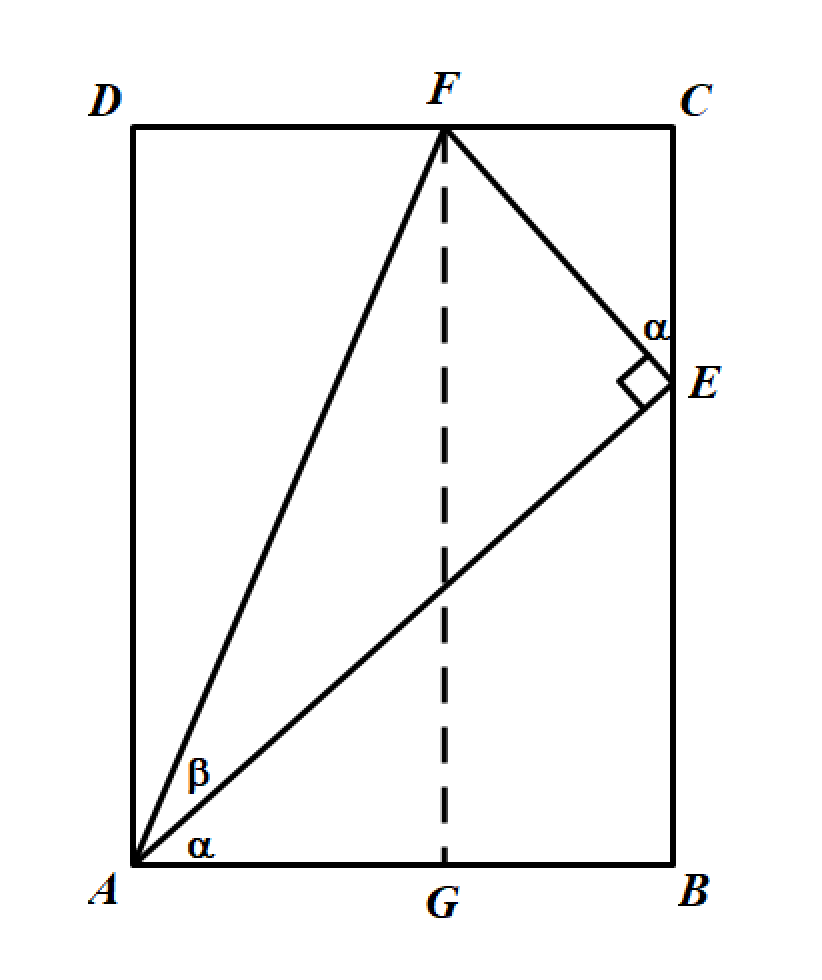
根据一线三等角模型,∠CEF=∠BAE\angle CEF=\angle BAE∠CEF=∠BAE,设 ∠CEF=∠BAE=α\angle CEF=\angle BAE=\alpha∠CEF=∠BAE=α,∠EAF=β\angle EAF=\beta∠EAF=β。则 ∠BAF=α+β\angle BAF=\alpha+\beta∠BAF=α+β。设 AF=xAF=xAF=x,则:
在△AEF中:{cosβ=AEAF=AEx⇒AE=xcosβsinβ=EFAF=EFx⇒EF=xsinβ在 \triangle AEF中: \begin{cases} \cos \beta = \dfrac{AE}{AF}=\dfrac{AE}{x} \Rightarrow AE=x\cos\beta\\ \sin \beta =\dfrac{EF}{AF}=\dfrac{EF}{x} \Rightarrow EF=x\sin \beta \end{cases} 在△AEF中:⎩⎨⎧cosβ=AFAE=xAE⇒AE=xcosβsinβ=AFEF=xEF⇒EF=xsinβ
类似地:
在△CEF中:{cosα=CEEF=CExsinβ⇒CE=xcosαsinβsinα=CFEF=CFxsinβ⇒CF=xsinαsinβ在 \triangle CEF中: \begin{cases} \cos \alpha=\dfrac{CE}{EF}=\dfrac{CE}{x\sin \beta}\Rightarrow CE=x\cos\alpha\sin\beta \\ \sin \alpha=\dfrac{CF}{EF}=\dfrac{CF}{x\sin \beta}\Rightarrow CF=x\sin\alpha\sin\beta \end{cases} \\ 在△CEF中:⎩⎨⎧cosα=EFCE=xsinβCE⇒CE=xcosαsinβsinα=EFCF=xsinβCF⇒CF=xsinαsinβ
同理:
在△ABE中:{cosα=ABAE=ABxcosβ⇒AB=xcosαcosβsinα=BEAE=BExcosβ⇒BE=xsinαcosβ在 \triangle ABE中: \begin{cases} \cos \alpha=\dfrac{AB}{AE}=\dfrac{AB}{x\cos \beta}\Rightarrow AB=x\cos\alpha\cos\beta \\ \sin \alpha=\dfrac{BE}{AE}=\dfrac{BE}{x\cos \beta}\Rightarrow BE=x\sin\alpha\cos\beta \end{cases} 在△ABE中:⎩⎨⎧cosα=AEAB=xcosβAB⇒AB=xcosαcosβsinα=AEBE=xcosβBE⇒BE=xsinαcosβ
因此,
在△AGF中:{sin(α+β)=GFAF=BCAF=BE+CEAF=xsinαcosβ+xcosαsinβx=sinαcosβ+cosαsinβcos(α+β)=AGAF=AB−GBAF=AB−CFAF=xcosαcosβ−xsinαsinβx=cosαcosβ−sinαsinβ在\triangle AGF中: \begin{cases} \sin(\alpha+\beta)&=\dfrac{GF}{AF}\\&=\dfrac{BC}{AF}\\&=\dfrac{BE+CE}{AF}\\&=\dfrac{x\sin\alpha\cos\beta +x\cos\alpha\sin\beta}{x}\\&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \cos(\alpha+\beta)&=\dfrac{AG}{AF}\\&=\dfrac{AB-GB}{AF}\\&=\dfrac{AB-CF}{AF}\\&=\dfrac{x\cos\alpha\cos\beta-x\sin\alpha\sin\beta}{x}\\&=\cos\alpha\cos\beta-\sin\alpha\sin\beta \end{cases} 在△AGF中:⎩⎨⎧sin(α+β)cos(α+β)=AFGF=AFBC=AFBE+CE=xxsinαcosβ+xcosαsinβ=sinαcosβ+cosαsinβ=AFAG=AFAB−GB=AFAB−CF=xxcosαcosβ−xsinαsinβ=cosαcosβ−sinαsinβ
至此,我们已经推出了两角和公式,两角差怎么推呢?根据上一期的诱导公式,cos(−β)=cosβ\cos (-\beta)=\cos \betacos(−β)=cosβ,sin(−β)=−sinβ\sin(-\beta)=-\sin \betasin(−β)=−sinβ。可以推得:
{sin(α−β)=sin(α+(−β))=sinαcos(−β)+cosαsin(−β)=sinαcosβ−cosαsinβcos(α−β)=cos(α+(−β))=cosαcos(−β)−sinαsin(−β)=cosαcosβ+sinαsinβ\begin{cases} \sin(\alpha-\beta)&=\sin(\alpha+(-\beta))\\&=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta)\\ &=\sin\alpha\cos\beta-\cos\alpha\sin\beta \\ \cos(\alpha-\beta)&=\cos(\alpha+(-\beta))\\&=\cos\alpha\cos(-\beta)-\sin\alpha\sin(-\beta)\\&=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{cases} ⎩⎨⎧sin(α−β)cos(α−β)=sin(α+(−β))=sinαcos(−β)+cosαsin(−β)=sinαcosβ−cosαsinβ=cos(α+(−β))=cosαcos(−β)−sinαsin(−β)=cosαcosβ+sinαsinβ
整理一下上面所有内容:
{sin(α±β)=sinαcosβ±cosαsinβcos(α±β)=cosαcosβ∓sinαsinβ\begin{cases} \sin(\alpha \pm \beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta \\ \cos(\alpha \pm \beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta \end{cases} {sin(α±β)=sinαcosβ±cosαsinβcos(α±β)=cosαcosβ∓sinαsinβ
这就是初中数学第二纯粹的力量:两角和差公式。
至此你已经可以算出 sin(15∘)=sin(45∘−30∘)=22×32−22×12=6−24\sin(15^{\circ})=\sin(45^{\circ}-30^\circ)=\dfrac{\sqrt 2}{2}\times\dfrac{\sqrt 3}{2}-\dfrac{\sqrt 2}{2}\times \dfrac{1}{2}=\dfrac{\sqrt 6-\sqrt 2}{4}sin(15∘)=sin(45∘−30∘)=22×23−22×21=46−2,以及其它如 105∘105^{\circ}105∘ 等角度的三角函数值。
二倍角公式
根据上述公式,我们可以对两倍角推出一个特殊的公式(直接把两个 α\alphaα 代入两角和公式即可,过程略):
{sin2α=2sinαcosαcos2α=cos2α−sin2α=2cos2α−1=1−2sin2α\begin{cases} \sin 2\alpha=2\sin\alpha\cos\alpha \\ \cos 2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha \end{cases} {sin2α=2sinαcosαcos2α=cos2α−sin2α=2cos2α−1=1−2sin2α
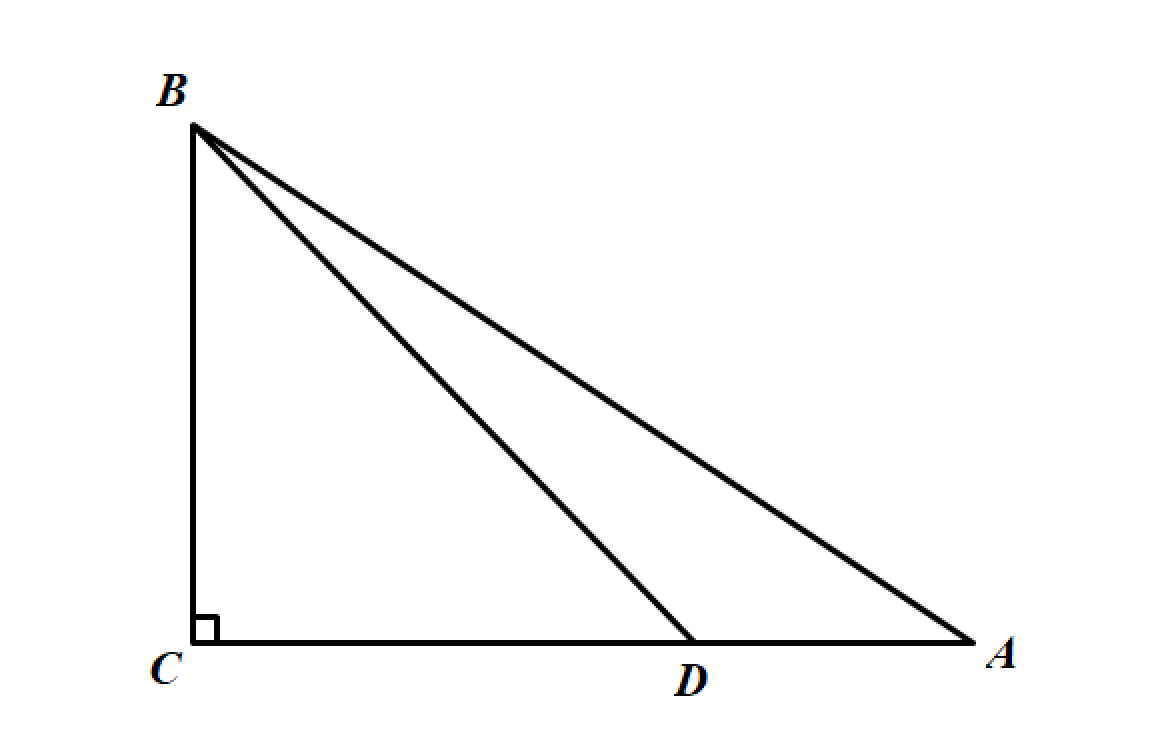
【例】如图,在 Rt△ABC\text{Rt} \triangle ABCRt△ABC 中,∠C=90∘\angle C=90^{\circ}∠C=90∘,AB=10AB=10AB=10,AC=8AC=8AC=8,∠CBD=2∠A\angle CBD=2\angle A∠CBD=2∠A,求 BDBDBD 的长。
解:
- 根据勾股定理,BC=6BC=6BC=6;
- 设 ∠A=α\angle A=\alpha∠A=α,则 ∠CBD=2α\angle CBD=2\alpha∠CBD=2α。cosα=ACAB=810=45\cos \alpha =\dfrac{AC}{AB}=\dfrac{8}{10}=\dfrac{4}{5}cosα=ABAC=108=54;
- 则 cos2α=2cos2α−1=2×1625−1=725\cos 2\alpha=2\cos^2\alpha-1=2\times\dfrac{16}{25}-1=\dfrac{7}{25}cos2α=2cos2α−1=2×2516−1=257;
- 所以,BCBD=725\dfrac{BC}{BD}=\dfrac{7}{25}BDBC=257,又因为 BC=6BC=6BC=6,所以 BD=25×67=1507BD=\dfrac{25\times 6}{7}=\dfrac{150}{7}BD=725×6=7150。
