线段树相关算法题(2)
hello 大家好,今天是2025年8月24日,我来继续给大家分享两道线段树相关的算法题。题目难度递增,学过线段树的朋友们可以来挑战一下。
前言(预备知识)
在解决线段树相关题目时,可以根据下面几个方面来记忆以及修改模板:
a. 根据查询以及修改操作,决定结构体中维护什么信息;
b. pushup:根据左右孩子维护的信息,更新当前结点维护的信息;
c. pushdown:当前结点的懒信息往下发一层,让左右孩子接收懒信息,并清空当前节点的懒信息
d. lazy:当前区间收到修改操作之后,更新当前结点维护的信息并且把修改信息“懒”下来;
e. build:遇到叶子结点返回,否则递归处理左右孩子,然后整合左右孩子的信息;
f. modify:遇到完全覆盖的区间,直接修改;否则有懒信息就先分给左右孩子懒信息,然后递归处 理左右区间;最后整合左右孩子的区间;
g. query:遇到完全覆盖的区间,直接返回节点维护的信息;否则有懒信息就先分给左右孩子懒信 息,然后整合左右区间的查询信息。
实现时候易错的细节问题:
a. lazy 函数只把懒信息存了下来,没有修改区间维护的信息;
b. query 以及 modify 操作,没有分配懒信息;
c. pushdown 之后,没有清空当前结点的懒标记。
线段树如果想要做到单次区间修改操作的时间复杂度为 log(n),那么在一段范围上执行修改 操作之后,需要能够在 O(1)时间内得到需要维护的信息。
题目一:贪婪大陆
题目链接:贪婪大陆
1:题目描述
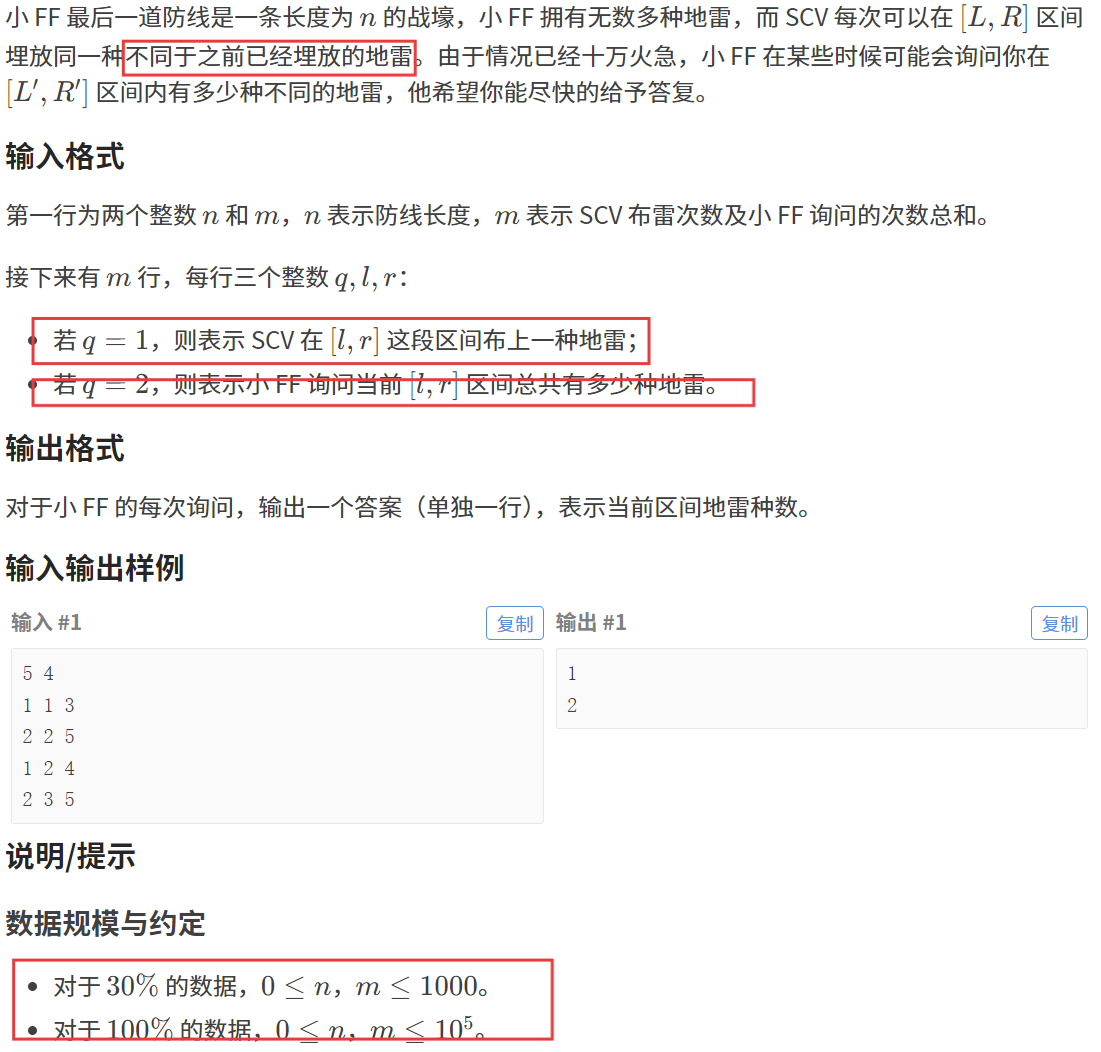
2:提炼经验(很重要)
如何快速求出【L,R】区间内的地雷的种类数???
我们可以利用求区间和时前缀和的思想:
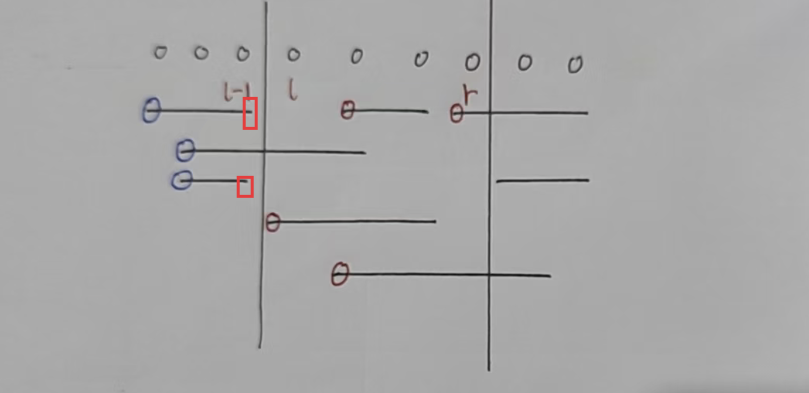
先求出【1,R】区间内,一共有多少种地雷。(起点数)(起点在 R 之前的都算)
再求出【1,L - 1】区间内,一共有多少种地雷。(终点数)(终点在 L 之前的都算)
最后做差,就可以求出【L,R】区间内,一共有多少种地雷。
3:算法原理
每增加一个地雷【L,R】,在 L 处加一个起点,在 R 处加一个终点。

那么,我们的问题就变成了:单点修改和区间查询了。
就可以使用线段树来解决:
step1. 结构体 node 中存储什么信息???
根据题目中的查询要求和我们的问题转化,显然我们需要维护一个区间的区间和。
区间中起点的个数和 & 区间中终点的个数和。
因此 node 当中维护的信息为:区间左端点、区间右端点、地雷起点个数和、地雷终点个数和
struct node
{int l, r, cnt1, cnt2;//cnt1表示:起点个数//cnt2表示:终点个数
}tr[N << 2];但是如果这样写的话,那么区间修改操作和区间查询操作就要实现两套代码:
关于起点的一套 & 关于终点的一套

优化:只用实现一套代码
struct node
{int l, r, cnt[2];//cnt[0]表示:起点个数//cnt[1]表示:终点个数
}tr[N << 2];这样写的话,在 modify 和 query 时,只需要多传入一个参数 k 就可以实现是修改查询 cnt[0] 还是cnt[1]。
step2. pushup 根据左右孩子维护的信息,更新当前结点维护的信息
已知左孩子的起点和终点个数和右孩子的起点和终点个数,就可以整合出当前区间的起点和终点个数。
void pushup(int p)
{tr[p].cnt[0] = tr[lc].cnt[0] + tr[rc].cnt[0];tr[p].cnt[1] = tr[lc].cnt[1] + tr[rc].cnt[1];
}step3. pushdown & lazy.(本题不需要)
因为这道题目并不涉及区间修改操作,因此不需要懒标记。
step4. build query……基本上都是模板,不再过多赘述了。
分析好上述问题之后,就可以尝试也代码了~~
4:代码实现
#include <iostream>using namespace std;#define lc p << 1
#define rc p << 1 | 1
const int N = 1e5 + 10;int n, m;struct node
{int l, r, cnt[2];//cnt[0]表示:起点个数//cnt[1]表示:终点个数
}tr[N << 2];void pushup(int p)
{tr[p].cnt[0] = tr[lc].cnt[0] + tr[rc].cnt[0];tr[p].cnt[1] = tr[lc].cnt[1] + tr[rc].cnt[1];
}void build(int p, int l, int r)
{tr[p] = {l, r, {0, 0}};if(l == r) return;int mid = (l + r) >> 1;build(lc, l, mid); build(rc, mid + 1, r);pushup(p);
}void modify(int p, int x, int k)
{int l = tr[p].l, r = tr[p].r;if(l == x && r == x){tr[p].cnt[k] += 1;return;}int mid = (l + r) >> 1;if(x <= mid) modify(lc, x, k);else modify(rc, x, k);pushup(p);
}int query(int p, int x, int y, int k)
{int l = tr[p].l, r = tr[p].r;if(x <= l && r <= y) return tr[p].cnt[k];int mid = (l + r) >> 1;int ret = 0;if(x <= mid) ret += query(lc, x, y, k);if(y > mid) ret += query(rc, x, y, k);return ret;
}int main()
{cin >> n >> m;build(1, 1, n);for(int i = 1; i <= m; i++){int op, x, y; cin >> op >> x >> y;if(op == 1){modify(1, x, 0); // 起点 modify(1, y, 1); // 终点 }else{cout << query(1, 1, y, 0) - query(1, 1, x - 1, 1) << endl;} }return 0;
}
题目二:无聊的数列
题目二:无聊的数列
1:题目描述

