OpenCV 图像边缘检测
目录
一、准备工作
二、Sobel 算子
1.Sobel 算子的使用方法
2.关键参数说明
三、Scharr 算子
1.Scharr 算子的使用方法
四、Laplacian 算子
1.Laplacian 算子的使用方法
2.cv2.Laplacian()函数参数说明:
五、Canny 边缘检测
1.Canny 边缘检测的使用方法
2.cv2.Canny()函数关键参数:
六、四种算子的对比分析
边缘检测是计算机视觉中的基础任务,它通过识别图像中灰度变化剧烈的区域来提取物体轮廓。本文将介绍 OpenCV 中四种常用的边缘检测算子:Sobel、Scharr、Laplacian 和 Canny,并通过实战代码展示它们的使用方法和效果差异。
一、准备工作
在开始之前,我们需要导入必要的库:
import cv2
import numpy as np
本文将使用一张老虎图像(tiger.jpg)作为示例,所有算子都将基于这张图像进行边缘检测实验。


二、Sobel 算子
Sobel 算子是一种常用的边缘检测算子,它通过计算图像在 x 和 y 方向的梯度来检测边缘。其原理是使用两个 3x3 的卷积核分别对图像进行卷积运算,得到 x 和 y 方向的边缘信息。
1.Sobel 算子的使用方法
# 以灰度模式读取图像
tiger = cv2.imread('tiger.jpg', 0)# Sobel计算x方向梯度,使用float64保存负数信息
tiger_x_64 = cv2.Sobel(tiger, cv2.CV_64F, dx=1, dy=0)
# 转换为绝对值,使负数边缘可见
tiger_x_full = cv2.convertScaleAbs(tiger_x_64)# Sobel计算y方向梯度
tiger_y_64 = cv2.Sobel(tiger, cv2.CV_64F, dx=0, dy=1)
tiger_y_full = cv2.convertScaleAbs(tiger_y_64)# 融合x、y方向梯度结果
tiger_xy_sobel_full = cv2.addWeighted(tiger_x_full, 1, tiger_y_full, 1, 0)# 显示结果
cv2.imshow('tiger_xy_sobel_full', tiger_xy_sobel_full)
cv2.waitKey(0)

2.关键参数说明
-
cv2.Sobel(src, ddepth, dx, dy):Sobel 算子的核心函数src:输入图像ddepth:输出图像深度,使用cv2.CV_64F可以保存负数信息dx:x 方向导数阶数(1 表示计算 x 方向梯度)dy:y 方向导数阶数(1 表示计算 y 方向梯度)
-
cv2.convertScaleAbs():将梯度结果转换为绝对值,确保负数边缘信息可见 -
cv2.addWeighted():加权融合 x 和 y 方向的边缘信息
三、Scharr 算子
Scharr 算子是 Sobel 算子的改进版本,当 Sobel 算子的卷积核大小为 3 时,Scharr 算子可以提供更精确的梯度计算结果。
1.Scharr 算子的使用方法
# 以灰度模式读取图像
tiger = cv2.imread('tiger.jpg', cv2.IMREAD_GRAYSCALE)# Scharr计算x方向梯度
tiger_x_64 = cv2.Scharr(tiger, cv2.CV_64F, dx=1, dy=0)
tiger_x_full = cv2.convertScaleAbs(tiger_x_64)# Scharr计算y方向梯度
tiger_y_64 = cv2.Scharr(tiger, cv2.CV_64F, dx=0, dy=1)
tiger_y_full = cv2.convertScaleAbs(tiger_y_64)# 融合x、y方向梯度结果
tiger_xy_Scharr_full = cv2.addWeighted(tiger_x_full, 1, tiger_y_full, 1, 0)# 显示结果
cv2.imshow('tiger_xy_Scharr_full', tiger_xy_Scharr_full)
cv2.waitKey(0)

Scharr 算子的使用方法与 Sobel 非常相似,只是将cv2.Sobel()替换为cv2.Scharr()。在边缘检测效果上,Scharr 算子通常比 Sobel 算子(3x3 核)更敏锐,能检测到更多细节。
四、Laplacian 算子
Laplacian 算子通过计算图像的二阶导数来检测边缘,它对噪声比较敏感,但能很好地检测出图像中的快速变化区域。
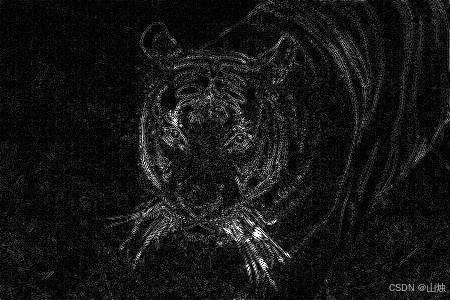
1.Laplacian 算子的使用方法
# 以灰度模式读取图像
tiger = cv2.imread('tiger.jpg', cv2.IMREAD_GRAYSCALE)# Laplacian算子处理
tiger_lap = cv2.Laplacian(tiger, cv2.CV_64F)
# 转换为绝对值
tiger_lap_full = cv2.convertScaleAbs(tiger_lap)# 显示结果
cv2.imshow('tiger_lap_full', tiger_lap_full)
cv2.waitKey(0)
2.cv2.Laplacian()函数参数说明:
src:输入图像depth:输出图像深度- 可选参数
ksize:滤波器孔径大小,必须为正奇数
Laplacian 算子不需要分别计算 x 和 y 方向的梯度,直接得到整体边缘信息,但实际应用中常与高斯模糊结合使用以减少噪声影响。
五、Canny 边缘检测
Canny 边缘检测是一种多阶段的边缘检测算法,具有良好的边缘检测效果和抗噪声能力,是实际应用中最常用的边缘检测方法之一。
1.Canny 边缘检测的使用方法
# 以灰度模式读取图像
tiger = cv2.imread('tiger.jpg', cv2.IMREAD_GRAYSCALE)# 显示原始灰度图像
cv2.imshow('tiger', tiger)
cv2.waitKey(0)# Canny边缘检测,设置阈值
tiger_canny = cv2.Canny(tiger, 150, 230)# 显示结果
cv2.imshow('tiger_canny', tiger_canny)
cv2.waitKey(0)

2.cv2.Canny()函数关键参数:
image:输入图像threshold1:低阈值,用于边缘连接threshold2:高阈值,用于检测强边缘
Canny 算法会自动处理梯度计算、非极大值抑制和边缘连接等步骤,通常能得到更清晰、连续的边缘结果。
六、四种算子的对比分析
- Sobel 算子:计算简单,速度快,对噪声有一定抑制能力,适合实时应用
- Scharr 算子:比 Sobel 算子(3x3)检测更精确,细节更丰富
- Laplacian 算子:对边缘响应更强烈,但对噪声敏感,边缘可能较粗
- Canny 算子:边缘检测效果最佳,边缘连续且定位准确,但计算复杂度较高
在实际应用中,可根据具体需求选择合适的边缘检测算子。对于大多数场景,Canny 边缘检测通常能提供最好的结果;而在实时性要求较高的场景,Sobel 算子可能是更好的选择。
