数据结构之深入探索归并排序
之前我们已经讲过了归并排序的递归实现,如果还没有学习的小伙伴们可以参考:数据结构之排序大全(4)-CSDN博客
外排序之文件归并排序的实现
外排序介绍
外排序(External sorting)是指能够处理极大量数据的排序算法。通常来说,外排序处理的数据不能一次装入内存,只能放在读写较慢的外存储器 (通常是硬盘) 上。外排序通常采用的是一种 “排序 - 归并” 的策略。在排序阶段,先读入能放在内存中的数据量,将其排序输出到一个临时文件,依此进行,将待排序数据组织为多个有序的临时文件。然后在归并阶段将这些临时文件组合为一个大的有序文件,也即排序结果。
跟外排序对应的就是内排序,我们之前讲的常见的排序,都是内排序,他们排序思想适应的是数据在内存中,支持随机访问。归并排序的思想不需要随机访问数据,只需要依次按序列读取数据,所以归并排序既是一个内排序,也是一个外排序。
文件归并排序思路分析
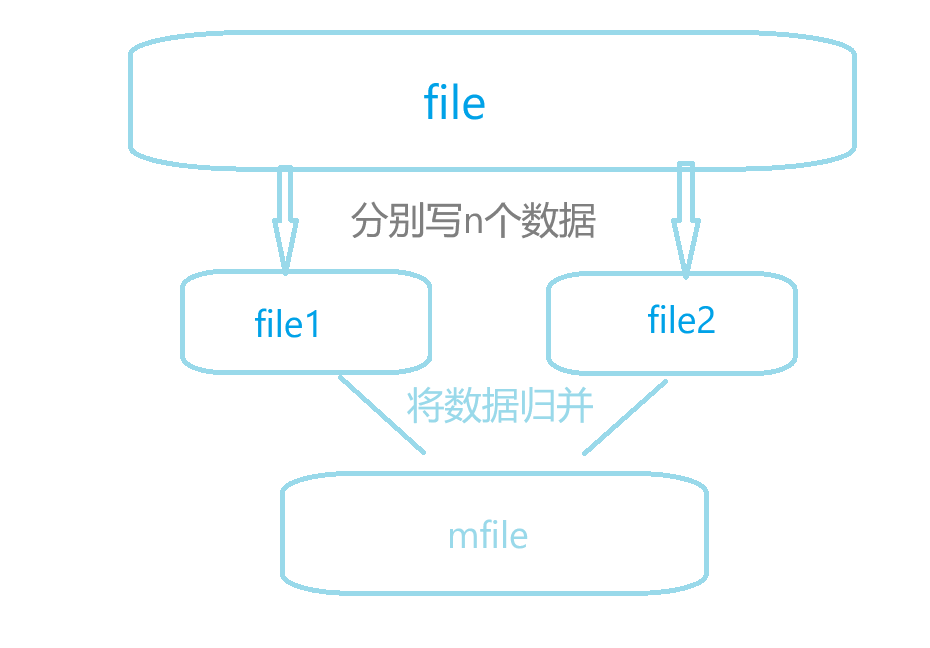
- 读取n个值排序后写到file1,再读取n个值排序后写到file2
- file1和file2利用归并排序的思想,依次读取比较,取小的尾插到mfile,mfile归并为一个有序文件
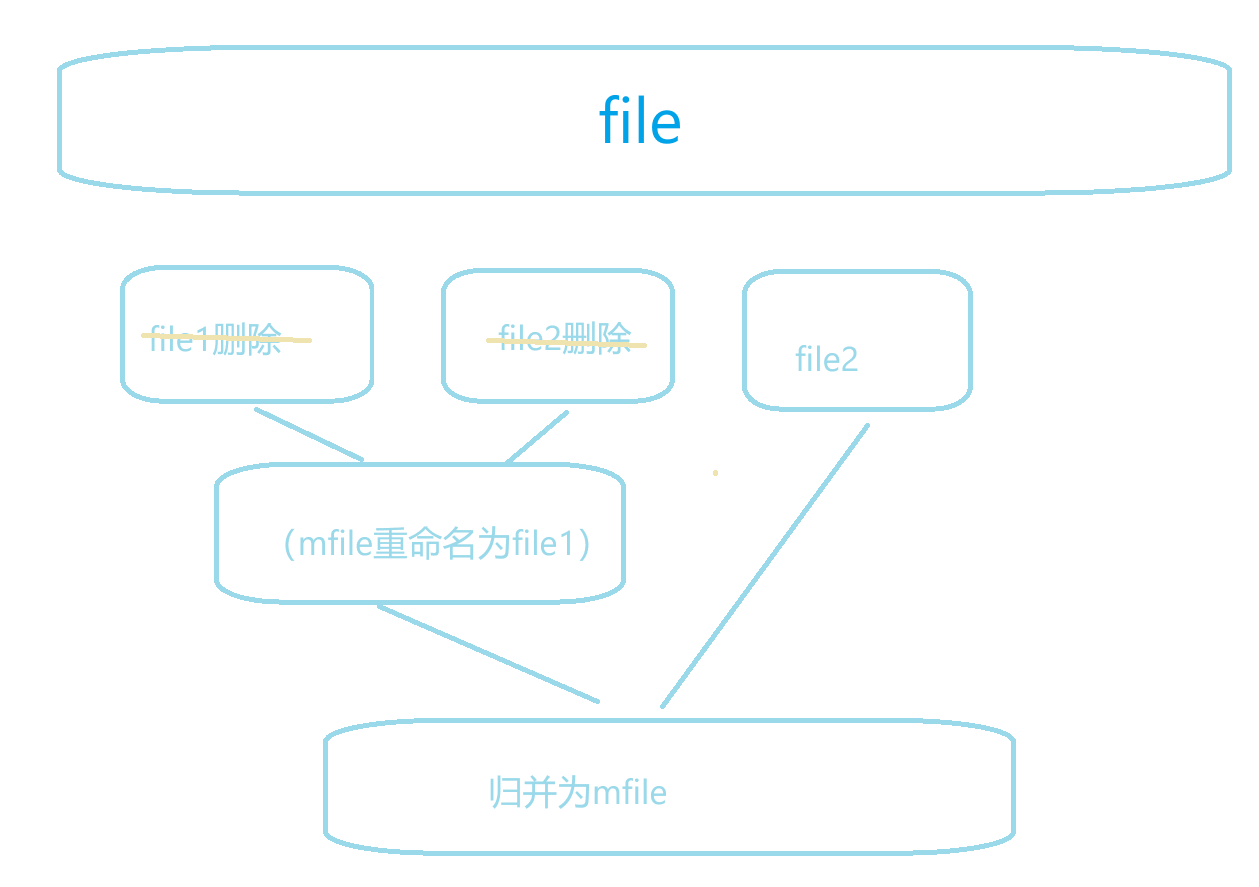
- 将file1和file2删掉,mfile重命名为file1
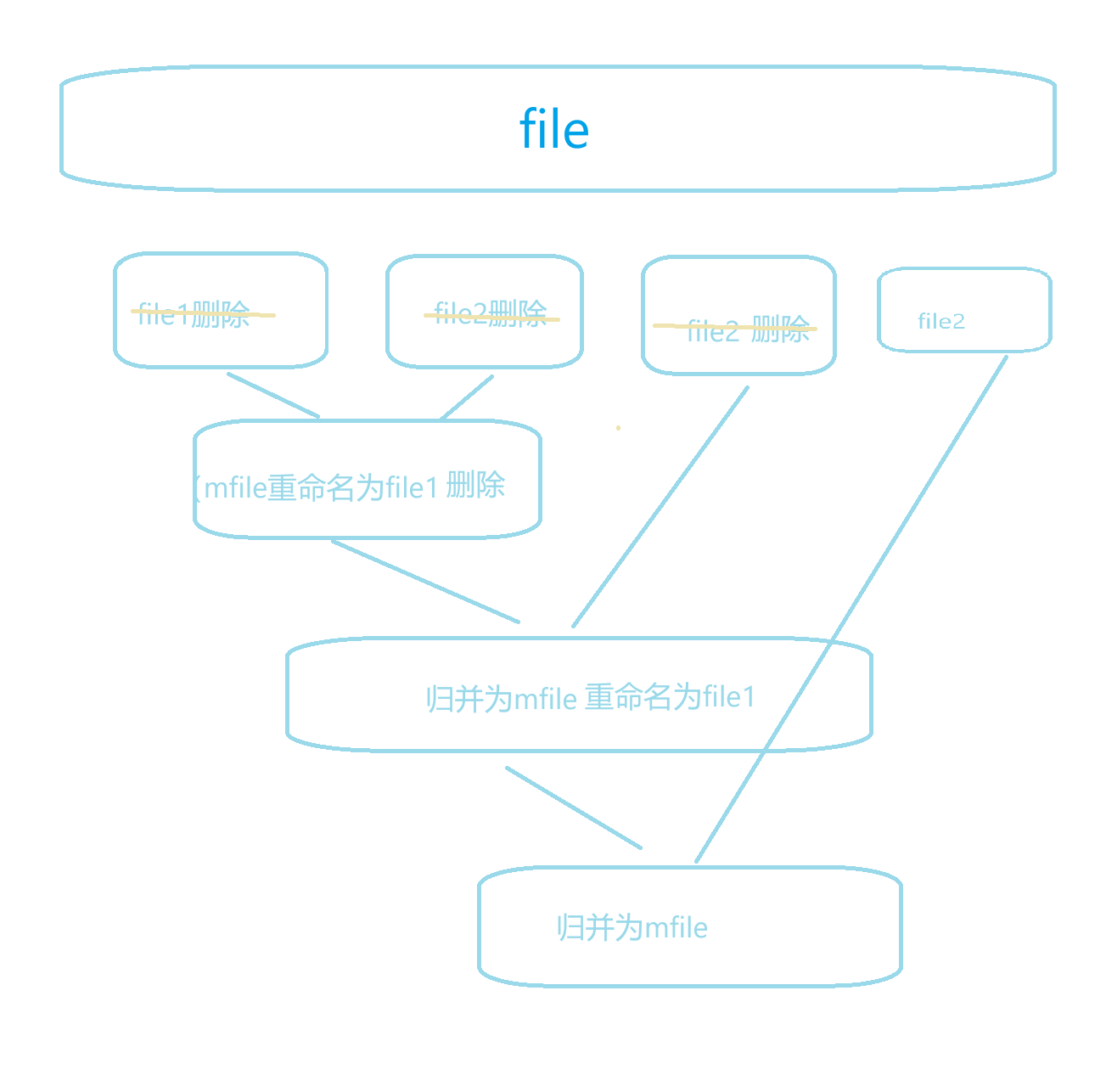
- 再次读取n个数据排序后写到file2
- 继续走file1和file2归并,重复步骤 2,直到文件中无法读出数据。最后归并出的有序数据放到了file1中
已经理解了文件归并排序的思想,那我们就来实现以下文件归并排序的代码吧:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>//造数据,将数据写入文件
void CreatData()
{//随机数种子srand((unsigned int)time(NULL));const char* filename = "data.txt";//打开文件——以写的方式打开FILE* pf = fopen(filename, "w");if (pf == NULL){perror("fopen fail");exit(1);}//可以向文件中写数据了int n = 1000;//表示数据个数int x;for (int i = 0; i < n; i++){x = rand() + i;fprintf(pf, "%d\n", x);}//关闭文件fclose(pf);pf = NULL;
}int cmp(const void* px, const void* py)
{return (*((int*)px) - *((int*)py));
}//从存放数据的文件中读取n个数据,并对所有读取到的数据进行排序
//从fout指向的文件中读取n个数据到file指向的文件中
//返回实际读取到的数据个数
int ReadNdataToFile(FILE* fout, int n, const char* file)
{//先读取n个数据到数组中,并对数组中的数据进行排序//创建数组int* arr = (int*)malloc(sizeof(int) * n);if (arr == NULL){perror("malloc fail");exit(2);}//读取数据//最多能读取的数据个数为nint num = 0;//表示数组中实际读到的数据个数int x;for (int i = 0; i < n; i++){if (fscanf(fout, "%d", &x) != EOF)//表示读取成功arr[num++] = x;}if (num == 0){free(arr);return 0;//表示没有读到数据}//对数组中的元素进行排序,这里我们使用库中的qsort函数qsort(arr, num, sizeof(int), cmp);//将排好序的数组中的元素写入file所指向的文件中//打开文件——以写的方式打开文件FILE* pf = fopen(file, "w");if (pf == NULL){free(arr);perror("fopen fail");exit(1);}for (int i = 0; i < num; i++){fprintf(pf, "%d\n", arr[i]);}free(arr);fclose(pf);pf = NULL;return num;
}void MergeFile(const char* file1, const char* file2, const char* mfile)
{//把三个文件打开FILE* fout1 = fopen(file1, "r");if (fout1 == NULL){perror("fopen fail");exit(3);}FILE* fout2 = fopen(file2, "r");if (fout2 == NULL){fclose(fout1);perror("fopen fail");exit(3);}FILE* fin = fopen(mfile, "w");if (fin == NULL){fclose(fout1);fclose(fout2);perror("fopen fail");exit(3);}//从file1和file2中读取数据并进行比较,哪个数据小就将哪个数据写到mfile文件中int x, y;int ret1 = fscanf(fout1, "%d", &x);int ret2 = fscanf(fout2, "%d", &y);while (ret1 != EOF && ret2 != EOF){if (x < y){fprintf(fin, "%d\n", x);ret1 = fscanf(fout1, "%d", &x);}else{fprintf(fin, "%d\n", y);ret2 = fscanf(fout2, "%d", &y);}}while (ret1 != EOF){fprintf(fin, "%d\n", x);ret1 = fscanf(fout1, "%d", &x);}while (ret2 != EOF){fprintf(fin, "%d\n", y);ret2 = fscanf(fout2, "%d", &y);}fclose(fout1);fclose(fout2);fclose(fin);
}int main()
{//创建文件,写数据//CreatData();const char* file1 = "file1.txt";const char* file2 = "file2.txt";const char* mfile = "mfile.txt";//打开总文件FILE* datapf = fopen("data.txt", "r");if (datapf == NULL){perror("fopen fail");exit(1);}//将排好序的数据分别写入file,file2int m = 100;ReadNdataToFile(datapf, m, file1);ReadNdataToFile(datapf, m, file2);//循环读取数据,直到读完所有数据while (1){//对file1和file2中的数据进行归并排序,归并后的数据写到mfile中MergeFile(file1, file2, mfile);//经过排序以后,mfile中的数据就是有序的了//删除file1,file2文件remove(file1);remove(file2);//将mfile重命名为file1rename(mfile, file1);//继续将data.txt中的数据读取到file2中,直到数据读取完毕int n = ReadNdataToFile(datapf, m, file2);if (n == 0)//表示数据已经读取完了{break;}}//结合上述过程,归并结果放在file1中return 0;
}代码看起来很长,但是整个代码的思路结合注释还是比较容易理解的,要是还有不清楚的地方欢迎在评论区提出哦。
归并排序的非递归版本
非递归版本的归并排序(迭代归并排序)是一种自底向上的排序方法,它避免了递归调用带来的开销。
核心思想
从最小单元开始,逐步合并相邻的有序序列:
-
初始状态:将每个元素视为一个长度为1的有序序列
-
逐步合并:每次将相邻的两个有序序列合并成一个更大的有序序列
-
翻倍增长:每次合并后,有序序列的长度翻倍(1→2→4→8→...)
-
最终合并:直到整个数组成为一个有序序列
看图理解非递归版本的思想:
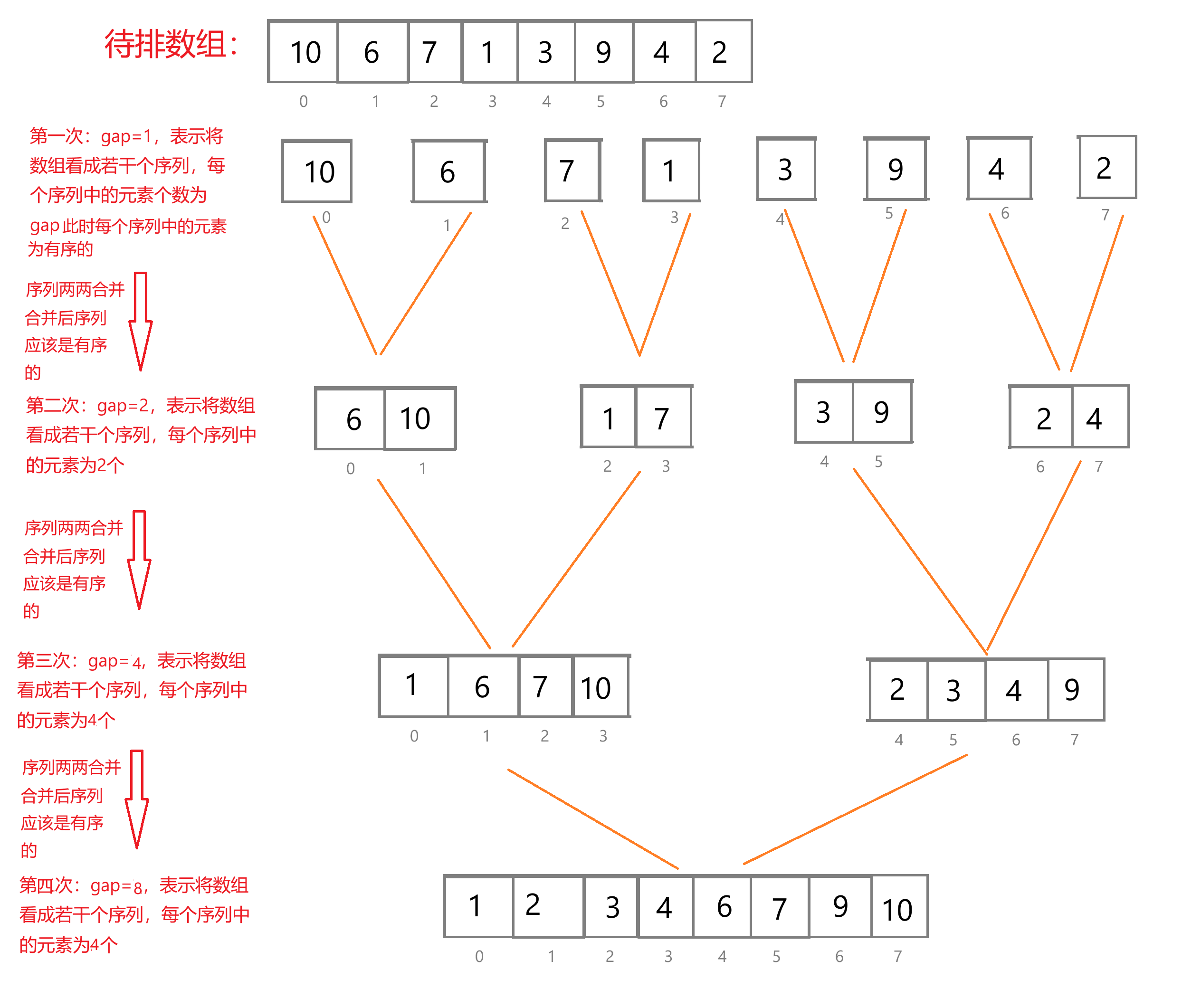
我们一起来写一下代码:
#include<stdlib.h>
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//初始子数组长度为1int gap = 1;while (gap < n){//i 就是当前某一对要合并的第一个子序列的起始位置,i初始为0,表示每一次都要先从数组arr的第一个位置开始合并//i+=gap表示对某一对序列完成合并后,要跳过合并后的整个序列,才能来到下一对要合并序列的起始位置for (int i = 0; i < n; i += (2 * gap)){//找到两个要合并序列各自的起始位置和终点位置,将这两个序列的值按顺序放到tmp数组中// 定义第一个子数组的边界 [begin1, end1]int begin1 = i, end1 = begin1 + gap - 1;// 定义第二个子数组的边界 [begin2, end2] int begin2 = begin1 + gap, end2 = begin2 + gap - 1;// 临时数组的索引,从当前归并段的开始位置int index = begin1;//合并两个子序列while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else {tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}// 将归并好的数据从临时数组拷贝回原数组for (int j = i; j <= end2; j++){arr[j] = tmp[j];}}// 子数组大小翻倍,进行下一轮归并gap *= 2;}free(tmp);
}我们用以下示例来测试一下代码:
#include<stdio.h>
int main()
{int arr1[] = { 10,6,7,1,3,9,4,2 };int sz1 = sizeof(arr1) / sizeof(arr1[0]);MergeSort(arr1, sz1);for (int i = 0; i < sz1; i++){printf("%d ", arr1[i]);}printf("\n");return 0;
}运行结果:
看上去代码好像没啥问题了,我们再来测试一组:
#include<stdio.h>
int main()
{int arr1[] = { 10,6,7,1,3,9,4,2 };int sz1 = sizeof(arr1) / sizeof(arr1[0]);int arr2[] = { 10,6,7,1,3,9,4 };int sz2 = sizeof(arr2) / sizeof(arr1[0]);MergeSort(arr2, sz2);for (int i = 0; i < sz2; i++){printf("%d ", arr2[i]);}printf("\n");return 0;
}运行结果:
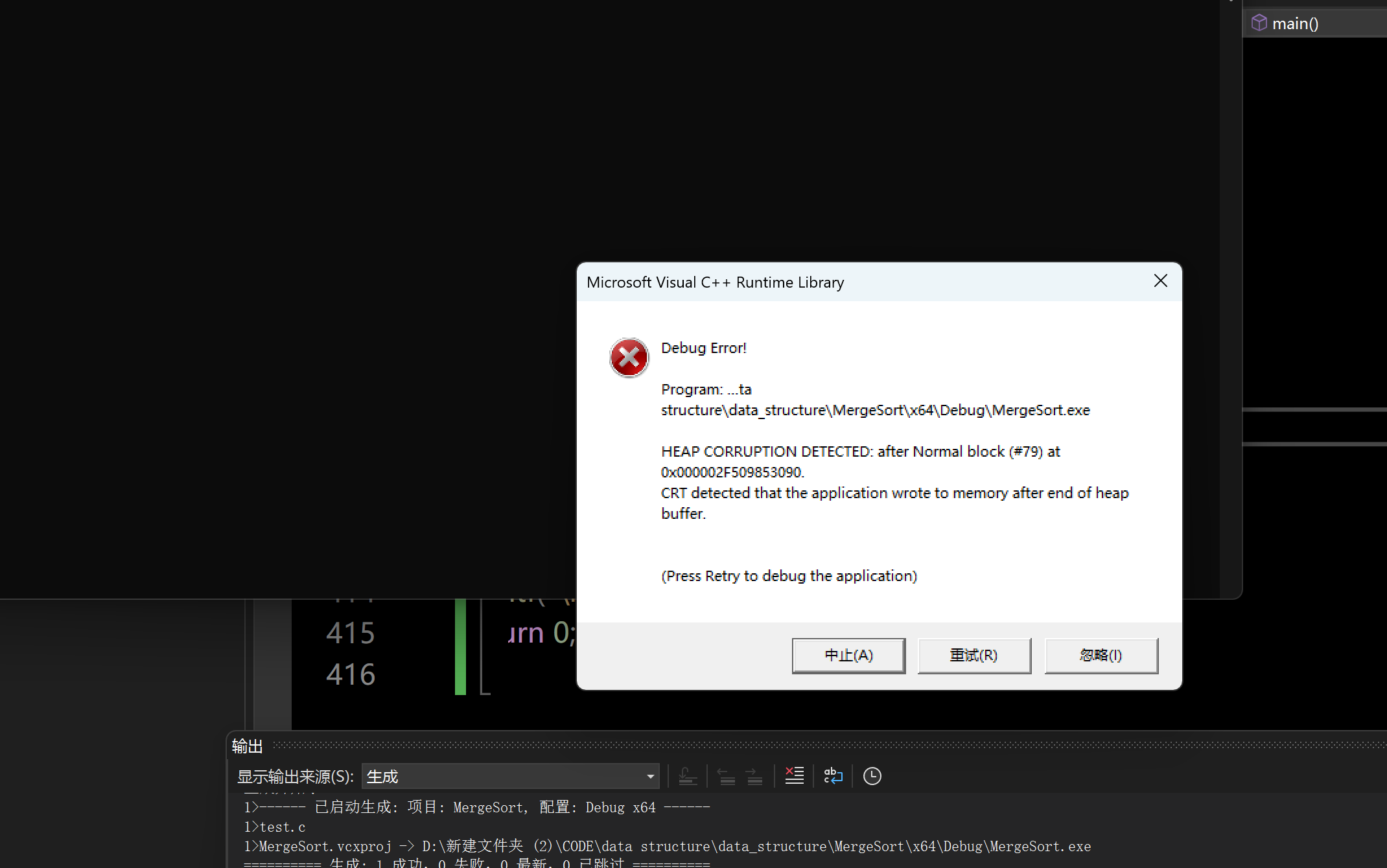
可以看到,运行时出错了,看上去应该是数组越界了,我们来分析一下问题:
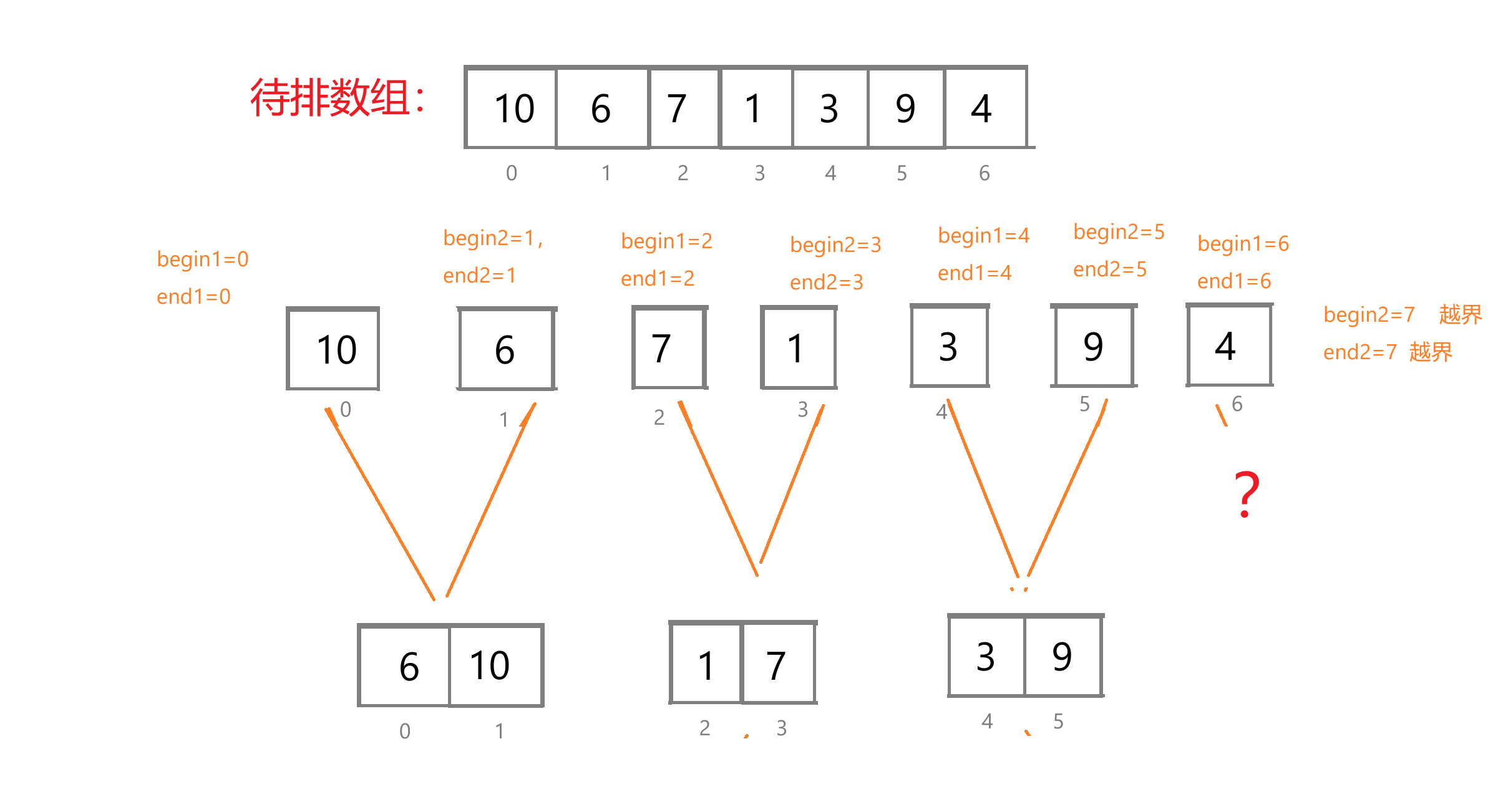
我们发现,当数组不能实现平均两两分组(必有一个序列落单时),就会出现下标越界的情况,上面就是begin2发生越界,也就说明在本轮合并过程中,不存在与4所对应的那个序列进行合并的序列(不存在成对的序列进行合并),那此时我们就不合并好了,直接增加一个判断条件:如果begin2越界,那就直接跳出循环。
解决了这个问题,我们看看往下演示是否还有其它问题:
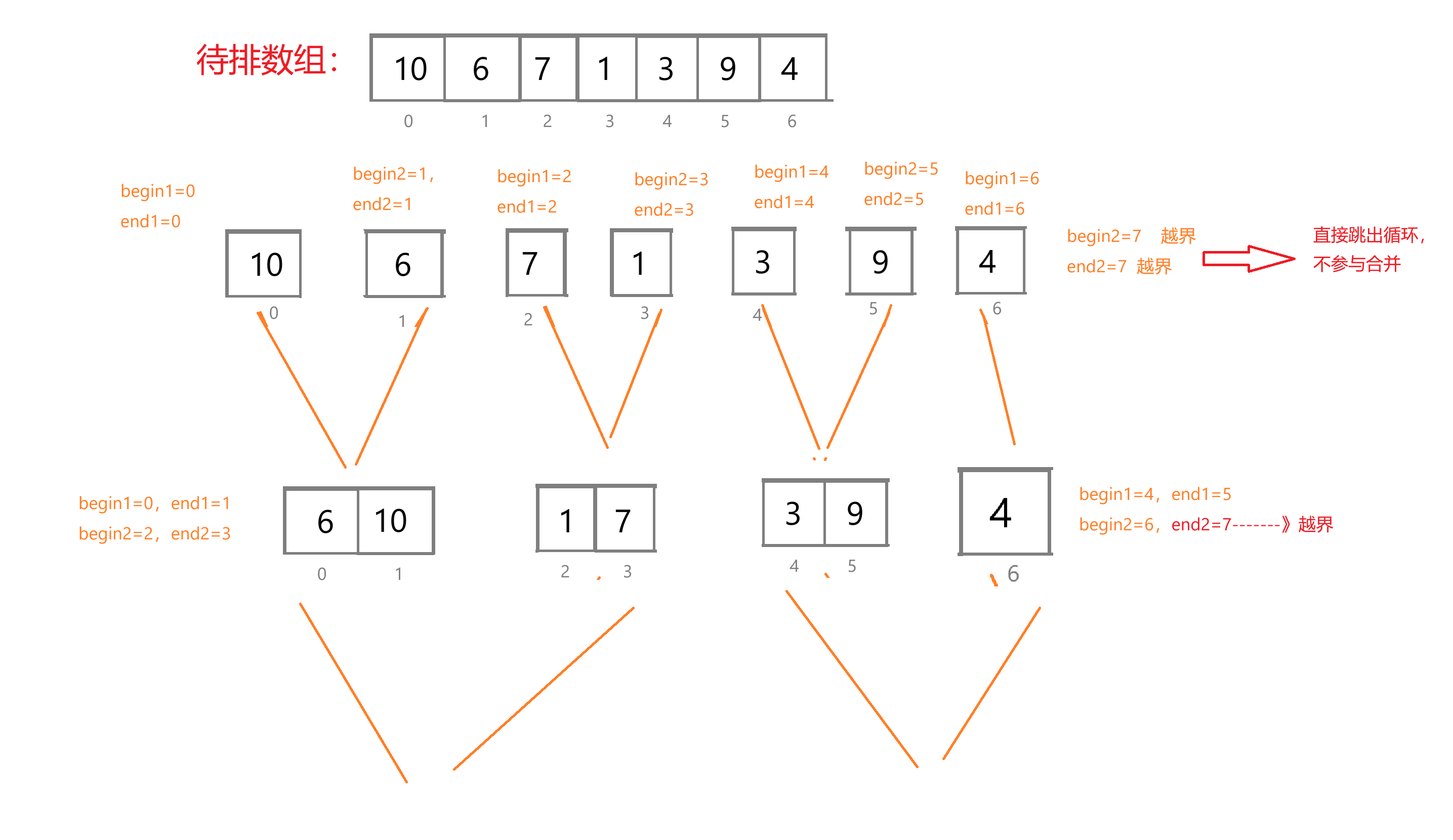
如图,在合并后面两个序列的过程中,end2再次发生越界,但此时begin2正常,begin2正常说明存在成对的序列进行合并,只是成对序列中的第二个序列中的元素不足gap个,所以end2越界,其实end2的实际值就是数组右边界n-1,那我们就再加一个判断条件就好了:
#include<stdlib.h>
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);//初始子数组长度为1int gap = 1;while (gap < n){//i 就是当前某一对要合并的第一个子序列的起始位置,i初始为0,表示每一次都要先从数组arr的第一个位置开始合并//i+=gap表示对某一对序列完成合并后,要跳过合并后的整个序列,才能来到下一对要合并序列的起始位置for (int i = 0; i < n; i += (2 * gap)){//找到两个要合并序列各自的起始位置和终点位置,将这两个序列的值按顺序放到tmp数组中// 定义第一个子数组的边界 [begin1, end1]int begin1 = i, end1 = begin1 + gap - 1;// 定义第二个子数组的边界 [begin2, end2] int begin2 = begin1 + gap, end2 = begin2 + gap - 1;if (begin2 > n-1)//begin2越界{break;}if (end2 > n - 1)//begin2未越界,end2越界,说明该一个序列中有数据,但是数据个数小于gap{end2 = n - 1;}// 临时数组的索引,从当前归并段的开始位置int index = begin1;//合并两个子序列while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else {tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}// 将归并好的数据从临时数组拷贝回原数组for (int j = i; j <= end2; j++){arr[j] = tmp[j];}}// 子数组大小翻倍,进行下一轮归并gap *= 2;}free(tmp);
}此时,再对数组进行排序就能达到预期效果了。
总结
现在为止,我们就已经讲完了初阶数据结构中排序算法的所有内容啦!!!完结撒花!!!但是我们还是需要总结一下排序的内容。
之前有关排序的博客链接:
数据结构之排序大全(1)-CSDN博客
数据结构之排序大全(1)-CSDN博客
数据结构之排序大全(3)-CSDN博客
数据结构之排序大全(4)-CSDN博客
数据结构之深入探索快速排序-CSDN博客
现在我们来了解一下什么叫排序算法的稳定性:
稳定性
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
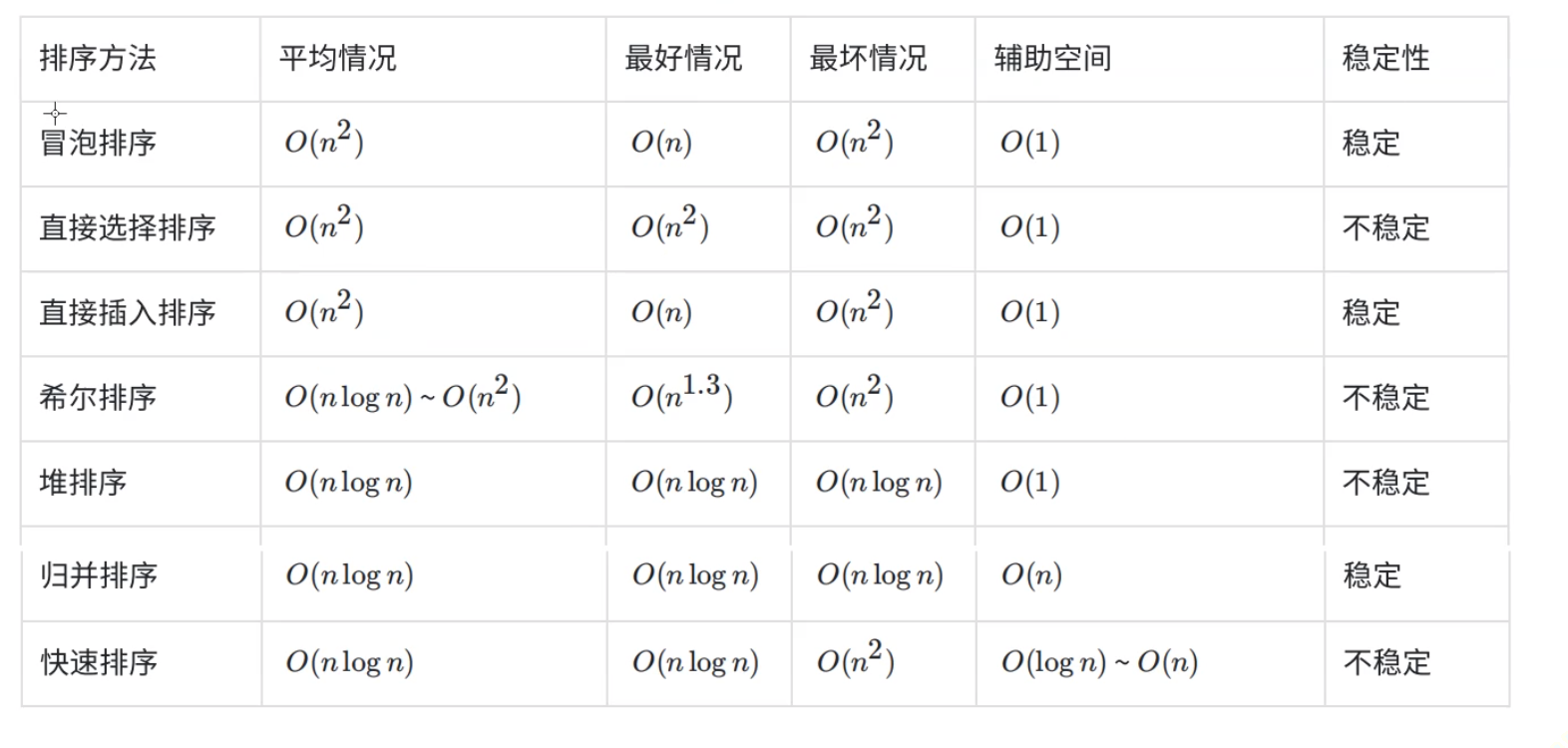
简单说一下算法稳定与否的原因:
| 冒泡排序 | 稳定 | 相等元素不交换 |
| 直接插入排序 | 稳定 | 相等元素不移动 |
| 归并排序 | 稳定 | 合并时相等元素取前面的 |
| 计数排序 | 稳定 | 维护相等元素的原始顺序 |
| 快速排序 | 不稳定 | 分区时可能改变相等元素顺序 |
| 直接选择排序 | 不稳定 | 交换可能改变相对顺序 |
| 堆排序 | 不稳定 | 堆化过程破坏稳定性 |
| 希尔排序 | 不稳定 | 分组插入破坏稳定性 |
小结:看到这里,我们的初阶数据结构排序算法的内容就基本完成了,完结撒花!!!
即使是最后一点内容了,朋友们也不要懈怠哦,记得空余时间多敲以下代码呢!!
喜欢小编的兄弟们欢迎三连哦,小编会继续更新编程方面的内容的。对于本节内容有任何问题的朋友欢迎在评论区留言哦!!!
