量子计算基础
量子计算
量子计算一般由三个基本步骤组成:制备输入量子态、对于量子态执行幺正变换以及测量输出态,这里将介绍这三个基本要素。
1 量子态
与经典计算中比特(bit)的概念相对应,量子计算中最小信息载体和处理单位是量子比特(quantum bit, or the qubit)。经典计算中,一个比特通过存储电平的高低来表示状态 0 或者状态 1。量子计算中,一个量子比特通过∣0⟩|0\rangle∣0⟩或∣1⟩|1\rangle∣1⟩态的线性组合描述来表示量子态,对应于两能级量子系统的基态和激发态,表示为 ∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle = \alpha |0\rangle + \beta |1\rangle∣ψ⟩=α∣0⟩+β∣1⟩。其中 α,β\alpha, \betaα,β称为振幅,是满足 ∣α∣2+∣β∣2=1|\alpha|^2 + |\beta|^2 = 1∣α∣2+∣β∣2=1 的复数。对于一个nnn量子比特系统,一个具有2n2^n2n个复数元素的向量xxx被用来表示2n2^n2n个基量子态的振幅,xxx中的所有元素满足∑i=02n∣xi∣2=1\sum_{i=0}^{2^n}|x_i|^2=1∑i=02n∣xi∣2=1。
一般将 ∣0⟩|0\rangle∣0⟩ 和 ∣1⟩|1\rangle∣1⟩ 写成以下列向量形式:
∣0⟩=[10],∣1⟩=[01]|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix},|1\rangle = \begin{bmatrix} 0 \\ 1 \end{bmatrix}∣0⟩=[10],∣1⟩=[01]
量子比特态的另一个表示方法是
∣ψ⟩=cos(θ/2)∣0⟩+eiφsin(θ/2)∣1⟩ |\psi\rangle = \cos(\theta/2)|0\rangle + e^{i\varphi}\sin(\theta/2)|1\rangle ∣ψ⟩=cos(θ/2)∣0⟩+eiφsin(θ/2)∣1⟩
其中 0≤ϕ<2π,0≤θ≤π0 \leq \phi < 2\pi, 0 \leq \theta \leq \pi0≤ϕ<2π,0≤θ≤π。量子比特态和单位球面上的点之间存在一一对应关系,这就是量子比特态的布洛赫球表示法。
下图即是布洛赫球:
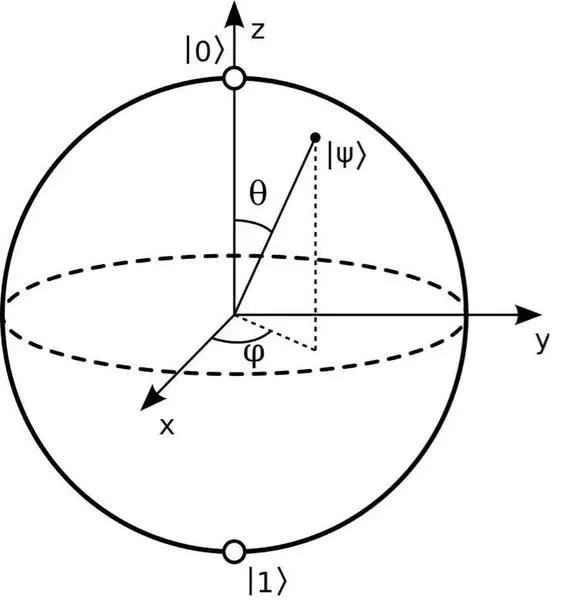
以下是几个特殊量子态在布洛赫球上的位置:
| 焦点 | θ\thetaθ | φ\varphiφ | ∣ψ⟩\vert\psi\rangle∣ψ⟩ |
|---|---|---|---|
| x轴 | π/2\pi/2π/2 | 000 | (∣0⟩+∣1⟩)/2(\vert0\rangle + \vert1\rangle)/\sqrt{2}(∣0⟩+∣1⟩)/2 |
| -x轴 | π/2\pi/2π/2 | π\piπ | (∣0⟩−∣1⟩)/2(\vert0\rangle - \vert1\rangle)/\sqrt{2}(∣0⟩−∣1⟩)/2 |
| y轴 | π/2\pi/2π/2 | π/2\pi/2π/2 | (∣0⟩+i∣1⟩)/2(\vert0\rangle + i\vert1\rangle)/\sqrt{2}(∣0⟩+i∣1⟩)/2 |
| -y轴 | π/2\pi/2π/2 | −π/2-\pi/2−π/2 | (∣0⟩−i∣1⟩)/2(\vert0\rangle - i\vert1\rangle)/\sqrt{2}(∣0⟩−i∣1⟩)/2 |
| z轴 | 000 | 000 | ∣0⟩\vert0\rangle∣0⟩ |
| -z轴 | π\piπ | 000 | ∣1⟩\vert1\rangle∣1⟩ |
2 量子门和量子线路
量子态之间的转换由幺正变换实现,可以通过量子线路来完成。量子线路由一系列量子门构成,量子门使量子态发生特定的演化。设初始量子态是ψ\psiψ,则经过酉变换U 演化的量子态是 ψ′=Uψ\psi'=U\psiψ′=Uψ。量子态的演化本质上可以看作是对量子态对应的向量做变换,即做矩阵的乘法。在数学上,我们使用酉矩阵表示量子逻辑门。对于所有的酉矩阵U,满足U†U=IU^{\dagger}U = IU†U=I。
(1)单比特量子逻辑门
作用于一个量子比特的门由一个 2×22\times22×2 的酉矩阵表示:
U(θ,ϕ,λ)=(cos(θ2)−eiλsin(θ2)eiϕsin(θ2)ei(ϕ+λ)cos(θ2))
U(\theta, \phi, \lambda) = \begin{pmatrix}
\cos\left(\frac{\theta}{2}\right) & -e^{i\lambda}\sin\left(\frac{\theta}{2}\right) \\
e^{i\phi}\sin\left(\frac{\theta}{2}\right) & e^{i(\phi+\lambda)}\cos\left(\frac{\theta}{2}\right)
\end{pmatrix}
U(θ,ϕ,λ)=(cos(2θ)eiϕsin(2θ)−eiλsin(2θ)ei(ϕ+λ)cos(2θ))
其中 0≤θ≤π0 \leq \theta \leq \pi0≤θ≤π ,0≤λ<2π0 \leq \lambda < 2\pi0≤λ<2π, 0≤ϕ<2π0 \leq \phi < 2\pi0≤ϕ<2π。
下面举例一些常见的单比特量子逻辑门。
I门
又称为Id门或者Identity门,是一种特殊的量子门,它对量子比特不进行任何操作,它在量子电路中相当于一个“占位符”,通常用于表示某个量子比特在某个步骤没有被操作。
I=[1001]I=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}I=[1001]
P门
又称为相位门,是可以设置参数的门。需要向其输入正确的数字(λ\lambdaλ)。P门是以Z轴为基准,旋转λ\lambdaλ。
p(λ)=[100eiλ]=U(0,0,λ)
p(\lambda) =
\begin{bmatrix}
1 & 0 \\
0 & e^{i\lambda}
\end{bmatrix}= U(0, 0, \lambda)
p(λ)=[100eiλ]=U(0,0,λ)
Hadamard门
也叫H门,常用于产生叠加量子态。
H=12(111−1)=U(π/2,0,π) H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} = U(\pi/2, 0, \pi) H=21(111−1)=U(π/2,0,π)
X门
也称为Pauli-X门或非门(NOT门),其作用是在Bloch球中以x轴为中心旋转 π\piπ,翻转量子比特的状态,即将∣0⟩|0\rangle∣0⟩状态变为∣1⟩|1\rangle∣1⟩状态,将∣1⟩|1\rangle∣1⟩状态变为∣0⟩|0\rangle∣0⟩状态。
X=Rx(π)=(0110)=U(π,0,π) X =R_x(\pi) = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} = U(\pi, 0, \pi) X=Rx(π)=(0110)=U(π,0,π)
Y门
Y门的作用是在Bloch球中以y轴为中心旋转 π\piπ。
Y=Ry(π)=(0−ii0)=U(π,π/2,π/2) Y =R_y(\pi) = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} = U(\pi, \pi/2, \pi/2) Y=Ry(π)=(0i−i0)=U(π,π/2,π/2)
Z门
Z门的作用是在Bloch球中以z轴为中心旋转 π\piπ。
Z=Rz(π)=(100−1)=P(π) Z =R_z(\pi) = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = P(\pi) Z=Rz(π)=(100−1)=P(π)
Rx门(绕x轴旋转门)
Rx门用于在Bloch球上绕x轴旋转量子比特的状态,其矩阵形式为:
Rx(θ)=(cos(θ/2)−isin(θ/2)−isin(θ/2)cos(θ/2)) R_x(\theta) = \begin{pmatrix} \cos(\theta/2) & -i\sin(\theta/2) \\ -i\sin(\theta/2) & \cos(\theta/2) \end{pmatrix} Rx(θ)=(cos(θ/2)−isin(θ/2)−isin(θ/2)cos(θ/2))
Ry门(绕y轴旋转门)
Ry门用于在Bloch球上绕y轴旋转量子比特的状态,其矩阵形式为:
Ry(θ)=(cos(θ/2)−sin(θ/2)sin(θ/2)cos(θ/2)) R_y(\theta) = \begin{pmatrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{pmatrix} Ry(θ)=(cos(θ/2)sin(θ/2)−sin(θ/2)cos(θ/2))
Rz门(绕z轴旋转门)
Rz门用于在Bloch球上绕z轴旋转量子比特的状态,其矩阵形式为:
Rz(θ)=(e−iθ/200eiθ/2) R_z(\theta) = \begin{pmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{pmatrix} Rz(θ)=(e−iθ/200eiθ/2)
(2)多比特量子逻辑门
CNOT门
作用于两个量子比特的量子门,当第一个量子比特(控制位)为 ∣1⟩|1\rangle∣1⟩的时候,对第二个量子比特施加一个X门的效果。 所以CNOT门在很多文献中也称为CX门。
CNOT=[1000010000010010]
CNOT = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
CNOT=1000010000010010
SWAP门
SWAP门用于交换两个量子比特的状态。
SWAP=[1000001001000001]
SW\kern-0.3emAP= \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
SWAP=1000001001000001
受控酉门
受控酉门的矩阵形式如下:
CU=[I00U]CU=\begin{bmatrix} I & 0 \\ 0 & U \end{bmatrix}CU=[I00U]
其中UUU为指定的酉操作。当控制量子比特是 ∣0⟩|0\rangle∣0⟩ 时,受控量子比特保持不变;当控制量子比特是 ∣1⟩|1\rangle∣1⟩ 时,受控量子比特做酉操作。以下是受控Z门(CZ门)的矩阵示例:
CZ=[100001000010000−1]
CZ = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & -1
\end{bmatrix}
CZ=100001000010000−1
3 量子测量
量子比特在经过量子线路的一系列幺正变换后,其状态无法直接读取,我们需要进行量子测量以获得结果。在量子力学中测量(measure)会导致量子态的坍缩,即从叠加态变为某个特定的本征态,因此量子状态的全部信息无法通过一次测量得到。测量为不可逆操作,不满足幺正变换。当对量子比特∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle = \alpha |0\rangle + \beta |1\rangle∣ψ⟩=α∣0⟩+β∣1⟩进行测量时,仅能得到该量子比特有∣α∣2|\alpha|^2∣α∣2的概率处在∣0⟩|0\rangle∣0⟩态,或有∣β∣2|\beta|^2∣β∣2的概率处在∣1⟩|1\rangle∣1⟩态。由于所有情况的概率和为1,则有∣α∣2+∣β∣2=1|\alpha|^2 + |\beta|^2 = 1∣α∣2+∣β∣2=1。
量子测量的过程可以通过一系列特定的测量算子{Mm}\{M_m\}{Mm}来描述,这些算子会作用在待测量系统的状态空间上,mmm表示可能的测量结果。假设测量前量子态的状态为∣ψ⟩|\psi\rangle∣ψ⟩,则得到测量结果m的概率为:
p(m)=⟨ψ∣Mm†Mm∣ψ⟩ p(m) = \langle \psi | M_m^\dagger M_m | \psi \rangle p(m)=⟨ψ∣Mm†Mm∣ψ⟩
测量后系统的状态塌缩为:
Mm∣ψ⟩⟨ψ∣Mm†Mm∣ψ⟩
\frac{M_m |\psi\rangle}{\sqrt{\langle \psi | M_m^\dagger M_m | \psi \rangle}}
⟨ψ∣Mm†Mm∣ψ⟩Mm∣ψ⟩
由于所有情况的概率和为1,即
1=∑mp(m)=∑m⟨ψ∣Mm†Mm∣ψ⟩
1=\sum_m p(m)=\sum_m\left\langle\psi\left|M_m^{\dagger} M_m\right| \psi\right\rangle
1=m∑p(m)=m∑⟨ψMm†Mmψ⟩
因此,测量算子需满足完备性方程(completeness equation):
∑mMm†Mm=I
\sum_m M_m^\dagger M_m = I
m∑Mm†Mm=I
例如单量子比特的测量。单量子比特在计算基下有两个测量算子,分别是M0=∣0⟩⟨0∣,M1=∣1⟩⟨1∣M_{0}=|0\rangle\left\langle 0\left|, M_{1}=\right| 1\right\rangle\langle 1|M0=∣0⟩⟨0∣,M1=∣1⟩⟨1∣。这两个测量算子都是自伴的,即
M0†=M0,M1†=M1 M_{0}^{\dagger}=M_{0}, M_{1}^{\dagger}=M_{1} M0†=M0,M1†=M1
且
M02=M0,M12=M1 M_{0}^{2}=M_{0}, M_{1}^{2}=M_{1} M02=M0,M12=M1
因此
M0†M0+M1†M1=M0+M1=I M_{0}^{\dagger} M_{0}+M_{1}^{\dagger} M_{1}=M_{0}+M_{1}=I M0†M0+M1†M1=M0+M1=I
该测量算子满足完备性方程。
设系统被测量时的状态是∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle=\alpha|0\rangle+\beta|1\rangle∣ψ⟩=α∣0⟩+β∣1⟩ ,测量结果为000的概率为
p(0)=⟨ψ∣M0†M0∣ψ⟩=⟨ψ∣M0∣ψ⟩=∣α∣2
p(0)=\left\langle\psi\left|M_{0}^{\dagger} M_{0}\right| \psi\right\rangle=\left\langle\psi\left|M_{0}\right| \psi\right\rangle=|\alpha|^{2}
p(0)=⟨ψM0†M0ψ⟩=⟨ψ∣M0∣ψ⟩=∣α∣2
对应测量后的状态为
M0∣ψ⟩⟨ψ∣M0†M0∣ψ⟩=M0∣ψ⟩∣α∣=α∣α∣∣0⟩
\frac{M_{0}|\psi\rangle}{\sqrt{\left\langle\psi\left|M_{0}^{\dagger} M_{0}\right| \psi\right\rangle}}=\frac{M_{0}|\psi\rangle}{|\alpha|}=\frac{\alpha}{|\alpha|}|0\rangle
⟨ψM0†M0ψ⟩M0∣ψ⟩=∣α∣M0∣ψ⟩=∣α∣α∣0⟩
测量结果为1的概率为
p(1)=⟨ψ∣M1†M1∣ψ⟩=⟨ψ∣M1∣ψ⟩=∣β∣2
p(1)=\left\langle\psi\left|M_{1}^{\dagger} M_{1}\right| \psi\right\rangle=\left\langle\psi\left|M_{1}\right| \psi\right\rangle=|\beta|^{2}
p(1)=⟨ψM1†M1ψ⟩=⟨ψ∣M1∣ψ⟩=∣β∣2
测量后的状态为
M1∣ψ⟩⟨ψ∣M1†M1∣ψ⟩=M1∣ψ⟩∣β∣=β∣β∣∣1⟩ \frac{M_{1}|\psi\rangle}{\sqrt{\left\langle\psi\left|M_{1}^{\dagger} M_{1}\right| \psi\right\rangle}}=\frac{M_{1}|\psi\rangle}{|\beta|}=\frac{\beta}{|\beta|}|1\rangle ⟨ψM1†M1ψ⟩M1∣ψ⟩=∣β∣M1∣ψ⟩=∣β∣β∣1⟩
量子测量有很多种方式,比如投影测量(projective measurements)、POVM测量(Positive Operator-Valued Measure)。
