算法训练营day52 图论③ 101.孤岛的总面积、102.沉没孤岛、103.水流问题、104.建造最大岛屿

        图论部分，继续岛屿问题

101.孤岛的总面积

        本题较为简单，可以增加一个预处理

        本题要求找到不靠边的陆地面积，那么我们只要从周边找到陆地然后 通过 dfs或者bfs 将周边靠陆地且相邻的陆地都变成海洋，然后再去重新遍历地图 统计此时还剩下的陆地就可以了。

深度搜索

        深度搜索中将岛屿标记进行修改来减少重复遍历的行为，但是这样破坏了数据的一致性，可以改为使用visit数组来判断，然后判断的时候可以不用同时使用，会造成冗余

position = [[1, 0], [0, 1], [-1, 0], [0, -1]]
count = 0def dfs(grid, x, y):global countgrid[x][y] = 0count += 1for i, j in position:next_x = x + inext_y = y + jif next_x < 0 or next_y < 0 or next_x >= len(grid) or next_y >= len(grid[0]):continueif grid[next_x][next_y] == 1: dfs(grid, next_x, next_y)n, m = map(int, input().split())# 邻接矩阵
grid = []
for i in range(n):grid.append(list(map(int, input().split())))# 清除边界上的连通分量
for i in range(n):if grid[i][0] == 1: dfs(grid, i, 0)if grid[i][m - 1] == 1: dfs(grid, i, m - 1)for j in range(m):if grid[0][j] == 1: dfs(grid, 0, j)if grid[n - 1][j] == 1: dfs(grid, n - 1, j)count = 0 # 将count重置为0
# 统计内部所有剩余的连通分量
for i in range(n):for j in range(m):if grid[i][j] == 1:dfs(grid, i, j)print(count)

广度搜索

        广度搜索中使用队列来实现

from collections import deque# 处理输入
n, m = list(map(int, input().split()))
g = []
for _ in range(n):row = list(map(int, input().split()))g.append(row)# 定义四个方向、孤岛面积（遍历完边缘后会被重置）
directions = [[0,1], [1,0], [-1,0], [0,-1]]
count = 0# 广搜
def bfs(r, c):global countq = deque()q.append((r, c))g[r][c] = 0count += 1while q:r, c = q.popleft()for di in directions:next_r = r + di[0]next_c = c + di[1]if next_c < 0 or next_c >= m or next_r < 0 or next_r >= n:continueif g[next_r][next_c] == 1:q.append((next_r, next_c))g[next_r][next_c] = 0count += 1for i in range(n):if g[i][0] == 1: bfs(i, 0)if g[i][m-1] == 1: bfs(i, m-1)for i in range(m):if g[0][i] == 1: bfs(0, i)if g[n-1][i] == 1: bfs(n-1, i)count = 0
for i in range(n):for j in range(m):if g[i][j] == 1: bfs(i, j)print(count)

102.沉没孤岛

        仍然是预处理的办法        

        思路依然是从地图周边出发，将周边空格相邻的陆地都做上标记，然后在遍历一遍地图，遇到 陆地 且没做过标记的，那么都是地图中间的 陆地 ，全部改成水域就行。

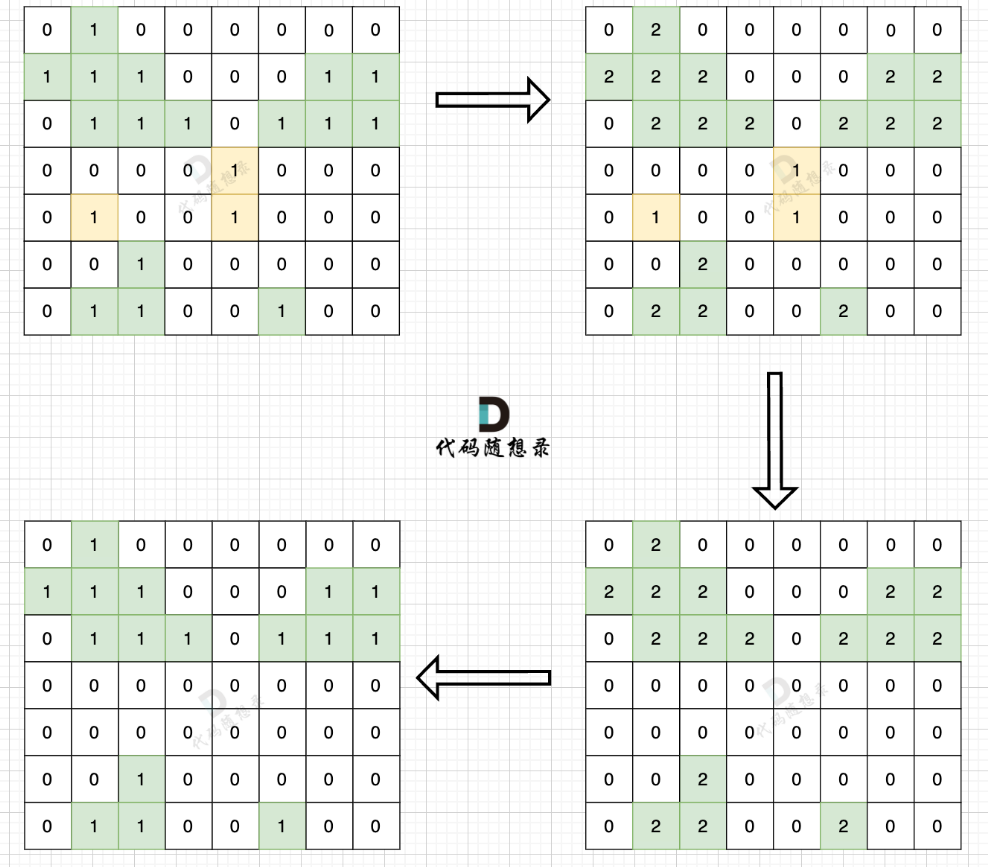
深度搜索

        整体思路不难，但是需要注意，对于矩阵的读入和写出问题

        字符串的 join 方法只能接收由字符串组成的可迭代对象（如字符串列表），所以需要map函数转换格式

def dfs(grid, x, y):grid[x][y] = 2directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]  # 四个方向for dx, dy in directions:nextx, nexty = x + dx, y + dy# 超过边界if nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]):continue# 不符合条件，不继续遍历if grid[nextx][nexty] == 0 or grid[nextx][nexty] == 2:continuedfs(grid, nextx, nexty)def main():n, m = map(int, input().split())grid = [[int(x) for x in input().split()] for _ in range(n)]# [int(x) for x in input().split()] 每行元素逐个改为int类型# 步骤一：# 从左侧边，和右侧边 向中间遍历for i in range(n):if grid[i][0] == 1:dfs(grid, i, 0)if grid[i][m - 1] == 1:dfs(grid, i, m - 1)# 从上边和下边 向中间遍历for j in range(m):if grid[0][j] == 1:dfs(grid, 0, j)if grid[n - 1][j] == 1:dfs(grid, n - 1, j)# 步骤二、步骤三for i in range(n):for j in range(m):if grid[i][j] == 1:grid[i][j] = 0if grid[i][j] == 2:grid[i][j] = 1# 打印结果for row in grid:print(' '.join(map(str, row)))if __name__ == "__main__":main()

103.水流问题

        这道题的普通思路就是遍历每个节点，对每个节点同时做一二边界的判断，遍历每一个节点，是 m * n，遍历每一个节点的时候，都要做深搜，深搜的时间复杂度是： m * n，那么整体时间复杂度 就是 O(m^2 * n^2) ，这是一个四次方的时间复杂度。

        优化的思路是逆向思维，可以从边界出发，一二边界同时覆盖的就是本题所求，因为visit数组的存在，会让重复的位置不会走第二次，这一点会对效率带来很大提升，所以本题整体的时间复杂度其实是： 2 * n * m + n * m ，所以最终时间复杂度为 O(n * m) 。（具体解释略）

        本题的关键地方在于增加对图论中搜索算法的时间复杂度分析

        strip()：移除字符串开头和结尾的空白字符（可以删去）

first = set()
second = set() # 保护性设置directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]def dfs(i, j, graph, visited, side):if visited[i][j]:returnvisited[i][j] = Trueside.add((i, j))for x, y in directions:new_x = i + xnew_y = j + yif (0 <= new_x < len(graph)and 0 <= new_y < len(graph[0])and int(graph[new_x][new_y]) >= int(graph[i][j])):dfs(new_x, new_y, graph, visited, side)def main():global firstglobal secondN, M = map(int, input().strip().split())graph = []for _ in range(N):row = input().strip().split()graph.append(row)# 是否可到达第一边界visited = [[False] * M for _ in range(N)]for i in range(M):dfs(0, i, graph, visited, first)for i in range(N):dfs(i, 0, graph, visited, first)# 是否可到达第二边界visited = [[False] * M for _ in range(N)]for i in range(M):dfs(N - 1, i, graph, visited, second)for i in range(N):dfs(i, M - 1, graph, visited, second)# 可到达第一边界和第二边界res = first & second  # 取交集for x, y in res:print(f"{x} {y}")if __name__ == "__main__":main()

104.建造最大岛屿

        这道题是有难度的，因为没有一个很直观的解法

        仍然是预处理的逻辑，剩下的内容就是遍历每个元素，相加周围四个数值即可

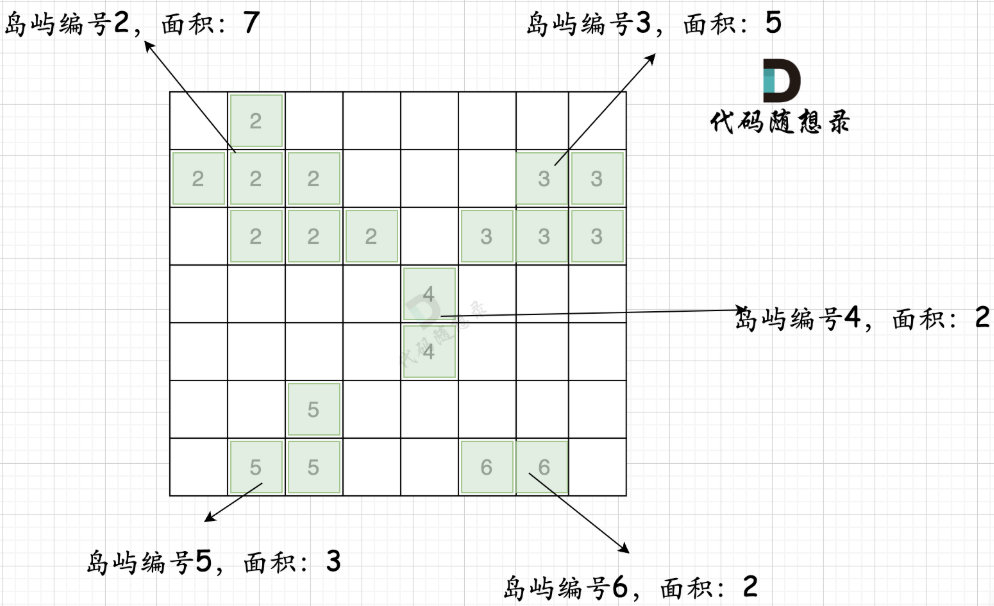
深度遍历

        需要注意visit数组不可缺少！防止存在两个相邻的同片岛屿重复相加

from typing import List  # 导入类型提示工具，用于指定参数类型
from collections import defaultdict  # 导入默认字典，方便统计岛屿面积class Solution:def __init__(self):# 定义四个方向的偏移量（下、上、右、左），用于遍历相邻单元格self.direction = [(1,0), (-1,0), (0,1), (0,-1)]self.res = 0  # 记录将海洋(0)转为陆地(1)后，能连接的最大岛屿总面积self.count = 0  # 临时计数：当前岛屿包含的单元格数量self.idx = 1  # 岛屿编号：从2开始（避免与原始的1/0冲突）# 用默认字典存储每个岛屿的面积：键是岛屿编号，值是该岛屿的单元格总数self.count_area = defaultdict(int)def max_area_island(self, grid: List[List[int]]) -> int:"""主函数：计算最大岛屿面积（含转换一个海洋为陆地后的可能情况）"""# 边界检查：如果网格为空，直接返回0if not grid or len(grid) == 0 or len(grid[0]) == 0:return 0# 第一步：遍历网格，用DFS标记所有独立岛屿（分配唯一编号）for i in range(len(grid)):  # 遍历每一行for j in range(len(grid[0])):  # 遍历每一列if grid[i][j] == 1:  # 发现未标记的陆地（原始值为1）self.count = 0  # 重置当前岛屿的计数self.idx += 1  # 岛屿编号+1（从2开始）self.dfs(grid, i, j)  # 深度优先搜索，标记整个岛屿# 第二步：统计每个岛屿的面积（单元格数量）self.check_area(grid)# 第三步：检查每个海洋单元格，计算转换后能连接的最大面积# 如果存在可连接的海洋（has_connect为True），返回"最大连接面积+1"（+1是转换的那个单元格）# 否则返回原始最大岛屿面积if self.check_largest_connect_island(grid=grid):return self.res + 1# 如果没有海洋（全是陆地），返回最大岛屿面积（注意排除0的统计）return max(self.count_area.values()) if self.count_area else 0def dfs(self, grid, row, col):"""深度优先搜索：标记岛屿并统计单元格数量"""# 将当前单元格标记为当前岛屿编号（覆盖原始的1）grid[row][col] = self.idxself.count += 1  # 该岛屿的单元格数量+1# 遍历四个方向的相邻单元格for dr, dc in self.direction:_row = dr + row  # 计算相邻单元格的行坐标_col = dc + col  # 计算相邻单元格的列坐标# 检查相邻单元格是否在网格范围内，且是未标记的陆地（值为1）if 0 <= _row < len(grid) and 0 <= _col < len(grid[0]) and grid[_row][_col] == 1:self.dfs(grid, _row, _col)  # 递归遍历相邻陆地returndef check_area(self, grid):"""统计每个岛屿编号对应的单元格数量（即岛屿面积）"""m, n = len(grid), len(grid[0])  # 获取网格的行数和列数# 遍历网格的每个单元格for row in range(m):for col in range(n):# 以单元格的值（岛屿编号或0）为键，累加出现次数（即面积）# get方法：如果键不存在，返回0；存在则返回当前值，然后+1self.count_area[grid[row][col]] = self.count_area.get(grid[row][col], 0) + 1returndef check_largest_connect_island(self, grid):"""检查每个海洋单元格，计算转换为陆地后能连接的最大岛屿面积"""m, n = len(grid), len(grid[0])has_connect = False  # 标记是否存在海洋单元格（0）# 遍历网格中的每个单元格for row in range(m):for col in range(n):if grid[row][col] == 0:  # 找到一个海洋单元格has_connect = True  # 标记存在可转换的海洋area = 0  # 临时存储当前海洋能连接的岛屿总面积visited = set()  # 记录已统计过的岛屿编号（避免重复计算）# 检查该海洋单元格的四个相邻方向for dr, dc in self.direction:_row = row + dr  # 相邻单元格的行坐标_col = col + dc  # 相邻单元格的列坐标# 检查相邻单元格是否在网格内，且是岛屿（非0），且未统计过if (0 <= _row < len(grid) and 0 <= _col < len(grid[0]) and grid[_row][_col] != 0 and grid[_row][_col] not in visited):visited.add(grid[_row][_col])  # 标记该岛屿已统计# 累加该岛屿的面积（从count_area字典中获取）area += self.count_area[grid[_row][_col]]# 更新最大连接面积self.res = max(self.res, area)return has_connect  # 返回是否存在海洋单元格def main():# 读取输入：第一行是网格的行数(m)和列数(n)m, n = map(int, input().split())grid = []# 读取m行数据，每行转换为整数列表，组成网格for i in range(m):grid.append(list(map(int, input().split())))# 创建Solution实例，计算并打印结果sol = Solution()print(sol.max_area_island(grid))if __name__ == '__main__':main()