cuda排序算法--双调排序(Bitonic_Sort)

1. 前言

本篇文章是CUDA系列之排序算法系列的双调排序，将详细介绍排序算法，并附带CUDA代码源码，下面我们来一睹为快

2. 双调排序原理

双调排序是data-independent的排序， 即比较顺序与数据无关的排序方法， 特别适合做并行计算，例如用GPU、fpga来计算。

2.1 双调序列

在讲双调排序之前，我们先需要了解什么是双调序列，双调排序就是递归排出若干个双调序列，然后进行merge，再排，再merge的步骤循环推进。
如果存在索引i，使得序列先单调递增后单调递减（或者先单调递减后单调递增，则数组A [0 … i … n]称为双调，即:
$$A[0]<A[1]<A[2]....A[i-1]<A[i]>A[i+1]>A[i+2]>A[i+3]>...>A[n]$$
其中，0 <= i <= n-1。双调排序的旋转也是双调。

2.2 Batcher定理

将任意一个长为2n的双调序列A分为等长的两半X和Y，将X中的元素与Y中的元素一一按原序比较，即a[i]与a[i+n] (i < n)比较，将较大者放入MAX序列，较小者放入MIN序列。则得到的MAX和MIN序列仍然是双调序列，并且MAX序列中的任意一个元素不小于MIN序列中的任意一个元素。

2.3 双调排序

将该序列划分成2个双调序列，然后继续对每个双调序列递归划分，得到更短的双调序列，直到得到的子序列长度为1为止。这时的输出序列按单调递增顺序排列。

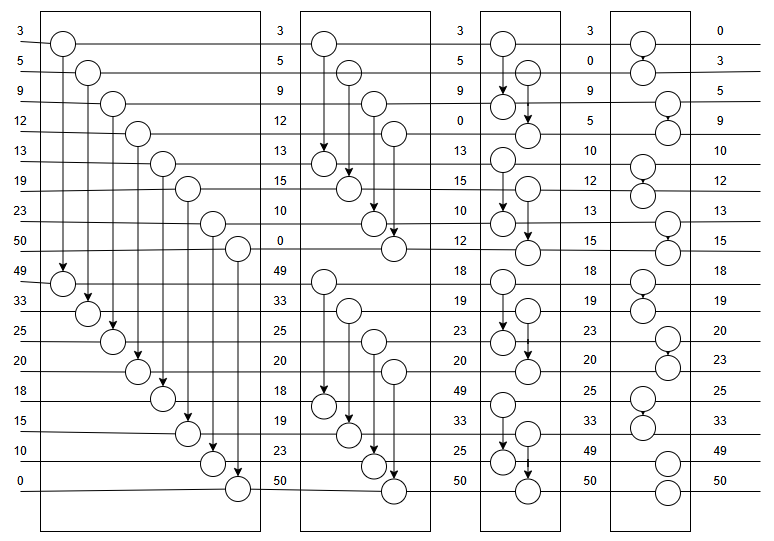
见下图：升序排序，具体方法是，把一个序列(1…n)对半分，假设n=2^k，然后1和n/2+1比较，小的放上，接下来2和n/2+2比较，小的放上，以此类推；然后看成两个(n/2)长度的序列，因为他们都是双调序列，所以可以重复上面的过程；总共重复k轮，即最后一轮已经是长度是2的序列比较了，就可得到最终的排序结果。

双调排序示意图：

2.4 任意序列生成双调序列

上面我们知道了如果有一个无序数列，根据batcher定理merge后就可以得到一个有序数列。那么要将一堆乱序序列排成有序序列，那么只需要先将无序数列排成双调序列，再根据Batcher定理就变成了有序序列，完成排序过程
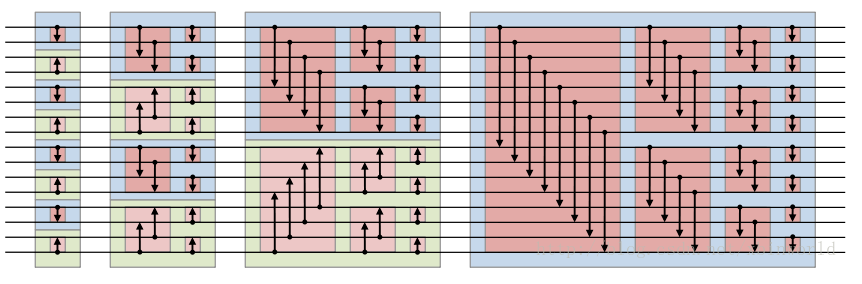
将无序数列排成双调序列的过程又被称之为Bitonic merge, 主要是采用分治的思想，正好是双调排序的逆过程，如下图所示：

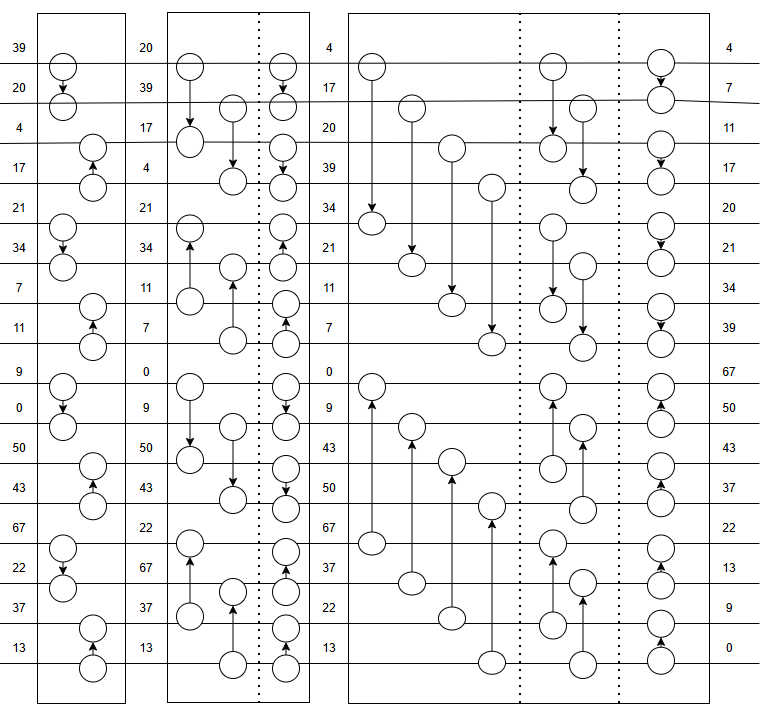
下面我们用一张示意图来展示Bitonic merge：

2.5 非2的幂次长度序列排序

这样的双调排序算法只能应付长度为2的幂的数组。那如何转化为能针对任意长度的数组呢？一个直观的方法就是使用padding。即使用一个定义的最大或者最小者来填充数组，让数组的大小填充到2的幂长度，再进行排序。最后过滤掉那些最大（最小）值即可。这种方式会使用到额外的空间，而且有时候padding的空间比较大（如数组长度为1025个元素，则需要填充到2048个，浪费了大量空间）。但是这种方法比较容易转化为针对GPU的并行算法。所以一般来说，并行计算中常使用双调排序来对一些较小的数组进行排序[3]。 如果要考虑不用padding，用更复杂的处理方法，参考[4] n!=2^k的双调排序网络，本文略。

3. CUDA 代码实现

constexpr int SHARED_SIZE_LIMIT = 1024 * 2;__device__ __forceinline__ void Comparator(uint &l_key, uint &l_val,uint &r_key, uint &r_val, uint dir) {if ((l_val > r_val && dir) || (l_val < r_val && !dir)) {uint key = l_key;l_key = r_key;r_key = key;uint val = l_val;l_val = r_val;r_val = val;}
}__global__ void bitonicSortShared(uint *dstKey, uint *dstVal, uint *srcKey,uint *srcVal, uint arrayLength, uint dir) {__shared__ uint s_key[SHARED_SIZE_LIMIT];__shared__ uint s_val[SHARED_SIZE_LIMIT];srcKey += blockIdx.x * SHARED_SIZE_LIMIT + threadIdx.x;srcVal += blockIdx.x * SHARED_SIZE_LIMIT + threadIdx.x;dstKey += blockIdx.x * SHARED_SIZE_LIMIT + threadIdx.x;dstVal += blockIdx.x * SHARED_SIZE_LIMIT + threadIdx.x;s_key[threadIdx.x] = srcKey[0];s_val[threadIdx.x] = srcVal[0];s_key[threadIdx.x + (SHARED_SIZE_LIMIT / 2)] =srcKey[(SHARED_SIZE_LIMIT / 2)];s_val[threadIdx.x + (SHARED_SIZE_LIMIT / 2)] =srcVal[(SHARED_SIZE_LIMIT / 2)];for (uint size = 2; size < arrayLength; size <<= 1) {uint ddd = dir ^ ((threadIdx.x & (size / 2)) != 0);for (uint stride = size / 2; stride > 0; stride >>= 1) {__syncthreads();uint pos = 2 * threadIdx.x - (threadIdx.x & (stride - 1));Comparator(s_key[pos + 0], s_val[pos + 0], s_key[pos + stride],s_val[pos + stride], ddd);}}// for the last bitonic merge stepfor (uint stride = arrayLength / 2; stride > 0; stride >>= 1) {__syncthreads();uint pos = 2 * threadIdx.x - (threadIdx.x & (stride - 1));Comparator(s_key[pos + 0], s_val[pos + 0], s_key[pos + stride],s_val[pos + stride], dir);}__syncthreads();dstKey[0] = s_key[threadIdx.x + 0];dstVal[0] = s_val[threadIdx.x + 0];dstKey[(SHARED_SIZE_LIMIT / 2)] =s_key[threadIdx.x + (SHARED_SIZE_LIMIT / 2)];dstVal[(SHARED_SIZE_LIMIT / 2)] =s_val[threadIdx.x + (SHARED_SIZE_LIMIT / 2)];
}// arrayLength <= SHARED_SIZE_LIMIT
extern "C" uint bitonicSort(uint *d_DstKey, uint *d_DstVal, uint *d_SrcKey,uint *d_SrcVal, uint batchSize, uint arrayLength,uint dir) {assert(arrayLength <= SHARED_SIZE_LIMIT);bitonicSortShared<<<batchSize, arrayLength / 2>>>(d_DstKey, d_DstVal, d_SrcKey, d_SrcVal, arrayLength, dir);return arrayLength;
}

本文只处理了arrayLength <= SHARED_SIZE_LIMIT, 当arrayLength > SHARED_SIZE_LIMIT时，可以多次利用该kernel，最后在global memory上做merge，所以就不在此追叙了，大家感兴趣的话，可以评论区交流。