博览会（树形DP）

题目描述

某市正在举行一场大型博览会，博览会有 n 个展馆，每个展馆里有若干个展台。这 n 个展馆以 及它们之间的道路可以看成一棵二叉树，博览会的出入口设在根节点——1 号展馆，小明将从这里 出发乘坐电瓶车到各个展馆参观，并最终回到 1 号展馆出口。
由于路程差异，乘坐电瓶车往返不同展馆间的费用也有所区别。出发时，小明的乘车卡里余额 为 k。他现在想知道，若全程都乘坐电瓶车，他最多能参观多少个展台？
说明：只要小明到达了某个展馆，就会参观该展馆内的所有展台，若多次参观同一个展台不重 复计算。

输入

输入共 n+2 行：
第 1 行为 2 个整数 n、k，用一个空格隔开，表示展馆个数和小明乘车卡初始余额。
第 2 行为 n 个数，用一个空格隔开，表示 1 号至 n 号各展馆的展台数目。
接下来 n 行，每行 4 个数，用一个空格隔开；第 i+2 行 4 个数分别表示展馆 i 左子节点展馆号、 到左子节点展馆的费用、右子节点展馆号、到右子节点展馆的费用。如果子节点展馆号为 0 则表示 没有对应的子节点展馆。

输出

输出共 1 行，1 个整数，表示小明最多能参观的展台数量。

样例输入

10 20
2 8 5 1 10 5 9 9 3 5
2 1 3 2
4 8 5 2
6 2 7 2
8 3 9 6 
0 0 10 2
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0

样例输出

39

提示

根据样例数据，可以得到如下展馆二叉树示意图（每个圈内标示了展馆号及展台数）：

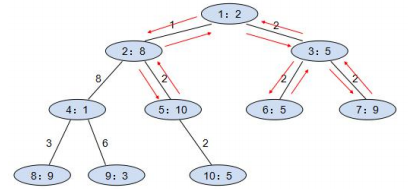
由图可知，小明沿红色箭号路径，到 1、2、5、3、6、7 这六个展馆参观并返回，往返乘车费用 为 18，参观展台数为 39，为能够实现的最大值。

对于 40%的数据：n≤10；k≤20；
对于 100%的数据：n≤50；k≤100；
所有展馆的展台总数不超过 。

思路分析

1.读入数据。展馆个数n，乘车卡初始余额k，exhibition_booth存储各展馆的站台数目，adj[u][1]记录展馆u的左子节点展馆号，fee[u][i]记录展馆 u 到左子节点展馆 i 的费用，adj[u][2]记录展馆u的右子节点展馆号，fee[u][j]记录展馆 u 到右子节点展馆 j 的费用。

2.深度优先搜索遍历二叉树结构，从根节点1开始。

3.dp[u][k]表示到达u节点、花费k元，最多能参观的展台数量。

4.深度优先搜索遍历树结构：

（1）对于节点u，dp[u][0]=exhibition_booth[u]。

（2）如果节点u有左子节点 l ：

深搜左子节点 l 。

l_cost为节点u到左子节点l的费用。

将当前节点u的DP状态复制到temp中。temp保存的是未加入左子树时的状态，即只包含当前节点u的展台数。

两层循环： 外层循环：j从总费用上限k递减到0，避免重复使用同一状态（类似于01背包的倒序）。 内层循环：x从0循环到 j - 2*l_cost，x表示在左子树内部使用的费用（注意，这里的费用已经是往返费用，即子树内部边的费用都已经按往返计算）。因为从u到左子树l需要往返费用2*l_cost（去一次，回来一次），所以剩余给左子树的费用不能超过j-2*l_cost。因此x的取值范围是0到j-2*l_cost。

条件判断：如果j - 2*l_cost - x < 0就跳过。

状态转移条件：检查temp[j - 2*l_cost - x]和dp[l][x]这两个状态是否有效：temp[j-2*l_cost-x]表示在未加入左子树时，当前节点u在剩余费用j-2*l_cost-x下的最大展台数；dp[l][x]表示左子树l在费用x下的最大展台数。如果两个状态都是有效的，那么就可以进行转移。

状态转移： 更新dp[u][j]：将当前节点u在剩余费用（j-2*l_cost-x）下的展台数（即temp[j-2*l_cost-x]）和左子树在费用x下的展台数（dp[l][x]）相加，然后与原来的dp[u][j]比较取最大值。

（3）如果节点u有右子节点 r ：

类似处理合并右子树。

5.遍历 j 从0到k，dp[1][j]中最大的即为小明最多能参观的展台数量。

代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int INF=1e9;
int n,k,exhibition_booth[51],a,b,c,d,fee[51][51],adj[51][3],ans;
vector<vector<int>>dp(55,vector<int>(105,-INF));
void dfs(int u){dp[u][0]=exhibition_booth[u];int l=adj[u][1];int l_cost=fee[u][l];if(l!=0){dfs(l);vector<int>temp=dp[u];for(int j=k;j>=0;j--){for(int x=0;x<=j-2*l_cost;x++){if(j-2*l_cost-x<0)continue;if(temp[j-2*l_cost-x]!=-INF&&dp[l][x]!=-INF){if(dp[u][j]<temp[j-2*l_cost-x]+dp[l][x]){dp[u][j]=temp[j-2*l_cost-x]+dp[l][x];}}}}}int r=adj[u][2];int r_cost=fee[u][r];if(r!=0){dfs(r);vector<int>temp=dp[u];for(int j=k;j>=0;j--){for(int y=0;y<=j-2*r_cost;y++){if(j-2*r_cost-y<0)continue;if(temp[j-2*r_cost-y]!=-INF&&dp[r][y]!=-INF){if(dp[u][j]<temp[j-2*r_cost-y]+dp[r][y]){dp[u][j]=temp[j-2*r_cost-y]+dp[r][y];}}}}}
}
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n>>k;for(int i=1;i<=n;i++){cin>>exhibition_booth[i];}for(int i=1;i<=n;i++){cin>>a>>b>>c>>d;if(a!=0){adj[i][1]=a;fee[i][a]=b;fee[a][i]=b;}if(c!=0){adj[i][2]=c;fee[i][c]=d;fee[c][i]=d;}}dfs(1);for(int i=0;i<=k;i++){ans=max(ans,dp[1][i]);}cout<<ans;return 0;
}