机器学习——多元线性回归
线性回归是统计学和机器学习中最基础、最广泛使用的预测方法之一,用于建立自变量(特征)与因变量(目标)之间的线性关系模型。
一、基本概念
1. 模型形式
一元线性回归是一种用于分析两个连续变量之间线性关系的统计方法。它通过建立一个线性方程来描述因变量(y)与一个自变量(x)之间的关系。其基本形式为:
y = β₀ + β₁x + ε
其中:
- y:因变量(响应变量),表示我们想要预测或解释的变量。
- x:自变量(解释变量),用于预测或解释因变量的变量。
- β₀:截距项(y-截距),表示当自变量x=0时,因变量y的期望值。
- β₁:斜率(回归系数),表示自变量x每增加一个单位,因变量y的期望变化量。
- ε:误差项(残差),表示模型未能解释的随机误差部分,通常假设其服从均值为0的正态分布。
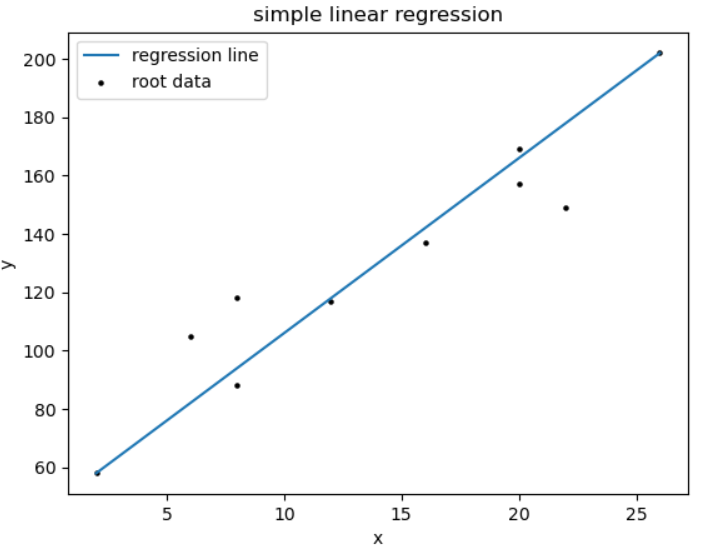
示例说明
假设我们想研究学习时间(x)与考试成绩(y)之间的关系:
- 如果回归方程为 ( y = 50 + 5x ),则:
- 截距β₀=50表示即使学习时间为0小时,预期成绩为50分(可能是基础分)。
- 斜率β₁=5表示每增加1小时学习时间,成绩平均提高5分。
多元线性回归(多变量)是一种用于分析多个自变量与一个因变量之间线性关系的统计方法,其基本模型可以表示为:
y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε
其中各参数的含义和特点如下:
y(因变量/目标变量):
- 这是我们要预测或解释的变量
- 在应用中,可以是房价、销售额、客户满意度评分等连续型变量
- 例如:预测房价时,y代表房屋的成交价格
x(自变量/特征/解释变量):
β₀(截距项):
β₁...βₙ(回归系数):
ε(误差项):
- 这些是用于预测或解释因变量的特征
- 可以是连续变量(如面积、年龄)或分类变量(如地区、品牌)
- 下标表示不同的特征,如x₁可能代表面积,x₂代表房龄等
- 示例:预测房价时,x₁可能是房屋面积(平方米),x₂可能是卧室数量
- 当所有自变量为0时,y的基准值
- 在实际情况中可能有物理意义,也可能只是数学上的截距
- 例如:在房价模型中,β₀可能代表土地的基础价值
- 表示每个自变量对因变量的影响程度
- 系数大小表示影响的幅度,符号表示影响的方向(正/负)
- 例如:β₁=500可能表示每增加1平方米,房价增加500元
- 代表模型无法解释的随机变异
- 通常假设服从正态分布N(0,σ²)
- 包含测量误差和遗漏变量的影响
应用场景举例:
- 市场营销:预测销售额(y)基于广告投入(x₁)、价格(x₂)、促销力度(x₃)
- 金融领域:评估贷款风险(y)基于收入(x₁)、信用评分(x₂)、负债比(x₃)
- 医疗研究:预测患者恢复时间(y)基于年龄(x₁)、治疗方案(x₂)、基础疾病(x₃)
模型建立步骤:
- 数据收集与清洗
- 特征选择与处理
- 模型拟合(通常使用最小二乘法)
- 模型评估(R²、调整R²、F检验等)
- 模型优化与验证
模型假设:
- 线性关系
- 自变量间无多重共线性
- 误差项同方差性
- 误差项无自相关
- 误差项正态分布
二、误差项分析
误差项分析是统计建模和计量经济学中的关键环节,主要用于评估模型拟合度及识别潜在问题。以下是扩展后的详细分析框架:
- 误差项的基本性质
- 随机性检验:通过Q-Q图或夏皮罗-威尔克检验验证是否服从正态分布
- 异方差检测:使用Breusch-Pagan检验或White检验(如金融数据常存在波动聚集性)
- 自相关分析:DW检验适用于时间序列数据(经济指标预测时需特别注意)
误差来源诊断 (1) 模型设定误差
- 遗漏变量:通过RESET检验或加入代理变量
- 错误函数形式:对比线性/对数线性模型的AIC值 (2) 测量误差
- 工具变量法处理内生性问题
- 企业财务报表数据常存在人为调整误差
处理方案
- 加权最小二乘法(WLS)处理异方差
- Cochran-Orcutt迭代法修正自相关
- 鲁棒标准误在Stata中的实现:reg y x, vce(robust)
应用场景示例
- 宏观经济预测:需同时检验截面相关性和时间相关性
- 临床试验数据:关注组间误差项的方差齐性
- 工程测量:采用误差传播定律分析系统误差
可视化辅助
- 残差散点图叠加Loess平滑曲线
- 使用R的car包生成残差诊断四象限图
- 动态时间序列误差图(包含3σ控制线)
注:在大数据场景下(n>10^5),建议采用分布式计算框架进行误差分析,如Spark MLlib的广义线性模型实现。对于高维数据(p>n),需结合正则化方法控制误差膨胀。
三、参数估计方法
1. 最小二乘法(OLS)
通过最小化残差平方和(RSS)来估计参数:
RSS = Σ(yᵢ - ŷᵢ)² = Σ(yᵢ - (β₀ + β₁xᵢ))²
求解方法:
解析解:β = (XᵀX)⁻¹Xᵀy(适用于特征数量较少时)
数值解:梯度下降等迭代方法(适用于大数据集)
2. 评估指标
R²(决定系数):模型解释的方差比例,0-1之间
调整R²:考虑自变量数量的修正R²
均方误差(MSE):Σ(yᵢ - ŷᵢ)²/n
均方根误差(RMSE):√MSE
平均绝对误差(MAE):Σ|yᵢ - ŷᵢ|/n
四、极大似然估计
极大似然估计(Maximum Likelihood Estimation,MLE)是统计学中最常用的参数估计方法之一,由英国统计学家R.A. Fisher在1912年提出。其核心思想是:在给定样本观测值的情况下,选择使得这些观测值出现概率最大的参数值作为估计值。
基本原理 设总体X的概率密度函数(连续型)或概率质量函数(离散型)为f(x;θ),其中θ为待估参数。对于独立同分布的样本X₁,X₂,...,Xₙ,其联合概率密度函数(似然函数)为: L(θ;x₁,x₂,...,xₙ) = ∏_{i=1}^n f(x_i;θ)
求解步骤 (1) 构造似然函数:根据观测数据写出似然函数表达式 (2) 取对数得到对数似然函数:ln L(θ) = ∑_{i=1}^n ln f(x_i;θ) (3) 对θ求导并令导数为零:∂ln L(θ)/∂θ = 0 (4) 解方程得到估计值θ̂
应用实例 例如在正态分布N(μ,σ²)中,对均值μ的MLE估计:
- 似然函数:L(μ,σ²) = (2πσ²)^(-n/2)exp[-∑(x_i-μ)²/(2σ²)]
- 对数似然函数:ln L = -n/2 ln(2πσ²) - ∑(x_i-μ)²/(2σ²)
- 求导可得:μ̂ = (1/n)∑x_i (样本均值)
特性 (1) 相合性:当样本量n→∞时,MLE依概率收敛于真实参数值 (2) 渐近正态性:√n(θ̂-θ₀) → N(0,I⁻¹(θ₀)),其中I(θ)是Fisher信息量 (3) 不变性:若θ̂是θ的MLE,则对任意函数g,g(θ̂)是g(θ)的MLE
注意事项 (1) 需要验证导数为零的点确实是最大值点 (2) 对于复杂模型,可能需要数值优化方法求解 (3) 在小样本情况下表现可能不佳
应用场景:广泛应用于回归分析、机器学习、计量经济学等领域,如逻辑回归的参数估计、时间序列模型的参数估计等。
五、线性回归的应用应用
LinearRegression( fit_intercept=True, normalize=False, copy_X=True, n_jobs=None, positive=False )
参数 | 类型 | 默认值 | 说明 |
|---|---|---|---|
| bool | True | 是否计算截距项 |
| bool | False | 是否在拟合前归一化特征(不推荐,建议使用StandardScaler) |
| bool | True | 是否复制X数据(否则可能被覆盖) |
| int | None | 用于计算的CPU核心数(-1表示使用所有核心) |
| bool | False | 是否强制系数为正 |
属性 | 类型 | 说明 |
|---|---|---|
| ndarray | 回归系数(特征权重) |
| float | 截距项(偏置) |
| int | 矩阵X的秩 |
| ndarray | X的奇异值 |
方法
fit(X, y, sample_weight=None)
拟合线性模型。
参数:
X: {array-like, sparse matrix} of shape (n_samples, n_features)训练数据
y: array-like of shape (n_samples,)目标值
sample_weight: array-like of shape (n_samples,), optional样本权重
返回:
self: object拟合后的模型实例
predict(X)
使用线性模型进行预测。
参数:
X: {array-like, sparse matrix} of shape (n_samples, n_features)预测样本
返回:
y_pred: ndarray of shape (n_samples,)预测值
score(X, y, sample_weight=None)
返回预测的确定系数R²。
参数:
X: array-like of shape (n_samples, n_features)测试样本
y: array-like of shape (n_samples,)真实目标值
sample_weight: array-like of shape (n_samples,), optional样本权重
返回:
score: floatR²分数
import pandas as pd
from sklearn.linear_model import LinearRegressiondata = pd.read_csv('糖尿病数据.csv')
corr = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()lrn = LinearRegression()
p_x=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']][:300]#切分
p_y=data[['target']][:300]t_x=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']][300:]
t_y=data[['target']][300:]lrn.fit(p_x,p_y)
pred_y = lrn.predict([ [-0.0454724779400257,-0.044641636506989,-0.0730303027164241,-0.081413765817132,0.0837401173882587,0.0278089295202079,0.17381578478911,-0.0394933828740919,-0.00421985970694603,0.00306440941436832]])
score = lrn.score(t_x,t_y)
print(pred_y)
print(score)