【递归、搜索与回溯算法】递归算法

- 递归算法简介
- 1. 递归是什么
- 2. 为什么会用到递归
- 3. 如何理解递归
- 4. 如何写好一个递归
- 一、[汉诺塔问题](https://leetcode.cn/problems/hanota-lcci/description/)
- 二、[合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)
- 三、[反转链表](https://leetcode.cn/problems/reverse-linked-list/description/)
- 四、[两两交换链表中的节点](https://leetcode.cn/problems/swap-nodes-in-pairs/description/)
- 五、[Pow(x, n)](https://leetcode.cn/problems/powx-n/description/)
- 结尾
递归算法简介
1. 递归是什么
递归是一种通过函数自身调用自身来解决问题的编程思想,核心是将一个复杂问题分解为与原问题结构相似但规模更小的子问题,直到子问题小到可以直接解决,最终通过子问题的解组合得到原问题的解。
2. 为什么会用到递归
递归之所以被广泛使用,核心原因在于它能将复杂问题简化,尤其适合解决具有自相似结构或嵌套层次的问题。
3. 如何理解递归
- 把递归函数当成一个黑盒
- 相信黑盒一定能够完成这个任务
4. 如何写好一个递归
- 先找到相同的子问题 --> 函数头的设计
- 只关心某一个子问题是如何解决的 --> 函数体的书写
- 注意一下函数出口
一、汉诺塔问题
题目描述:

思路讲解:
本道题需要我们用栈将所有盘子从第一根柱子移到最后一根柱子,下面我就模拟一下该如何移动盘子才能完成目的。这里我设盘子的个数为N。
- 当A上有一个盘子的时候,我们只需要将这一个盘子移动到C即可
- 当A上有两个盘子的时候,我们需要先将这一最大的盘子移动到C
- 将一个(2-1)个盘子借助C移动到B上
- A上还剩一个最大的盘子,将它直接移动到C上
- 再将B上的一个(2-1)盘子借助A移动到C上,由于C上的是最大的盘子,可以叠加其他任意盘子,这一步就可以转化为当B上有一个盘子的时候,需要将这一个盘子移动到C
- 当A上有三个盘子的时候,我们需要先将这一最大的盘子移动到C
- 将一个(3-1)个盘子借助C移动到B上
- A上还剩一个最大的盘子,将它直接移动到C上
- 再将B上的一个(3-1)盘子借助A移动到C上,由于C上的是最大的盘子,可以叠加其他任意盘子,这一步就可以转化为当B上有两个盘子的时候,需要将这些盘子移动到C
- 当A上有四个盘子的时候,我们需要先将这一最大的盘子移动到C
- 将一个(4-1)个盘子借助C移动到B上
- A上还剩一个最大的盘子,将它直接移动到C上
- 再将B上的一个(4-1)盘子借助A移动到C上,由于C上的是最大的盘子,可以叠加其他任意盘子,这一步就可以转化为当B上有三个盘子的时候,需要将这些盘子移动到C
- 当A上有n个盘子的时候,我们需要先将这一最大的盘子移动到C
- 将一个(n-1)个盘子借助C移动到B上
- A上还剩一个最大的盘子,将它直接移动到C上
- 再将B上的一个(n-1)盘子借助A移动到C上,由于C上的是最大的盘子,可以叠加其他任意盘子,这一步就可以转化为当B上有n-1个盘子的时候,需要将这些盘子移动到C
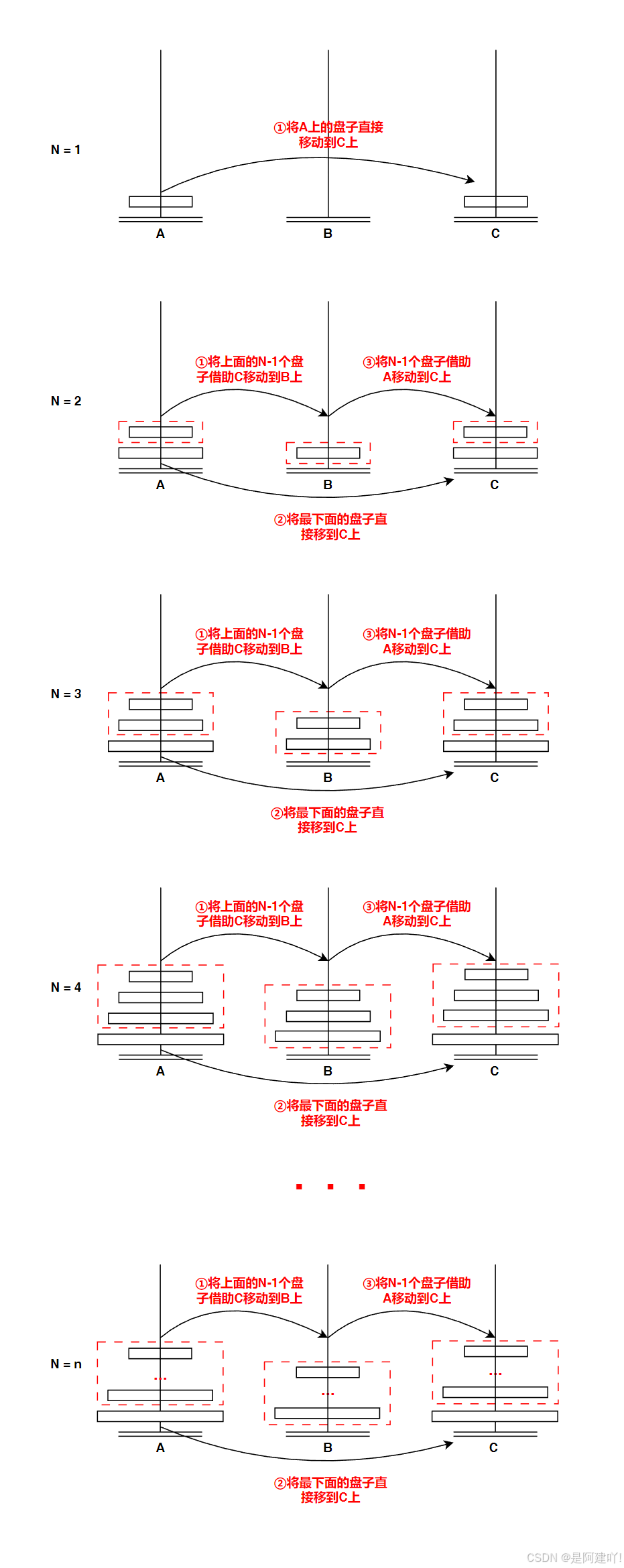
通过上面的模拟我们发现完成大问题时,会遇到相同的子问题,这就满足了使用递归的条件。以下是具体思路:
- 终止条件:
- 当 n = 1 时(只有 1 个盘子),直接将盘子从 A 移到 C,无需递归
- 问题分解:
- 要将 n 个盘子从柱子 A 移到柱子 C(借助柱子 B),可以拆分为 3 步:
- 将 n-1 个盘子从 A 移到 B(借助 C 作为过渡)
- 将第 n 个盘子(最大的盘子)从 A 直接移到 C
- 将 n-1 个盘子从 B 移到 C(借助 A 作为过渡)
- 要将 n 个盘子从柱子 A 移到柱子 C(借助柱子 B),可以拆分为 3 步:
- 递归调用:
- 每次递归减少一个盘子,直到问题简化为移动单个盘子
编写代码:
class Solution {
public:void dfs(vector<int>& A, vector<int>& B, vector<int>& C , int num){if(num == 1){C.push_back(A.back());A.pop_back();return;}dfs(A,C,B,num-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,num-1);}void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}
};
二、合并两个有序链表
题目描述:
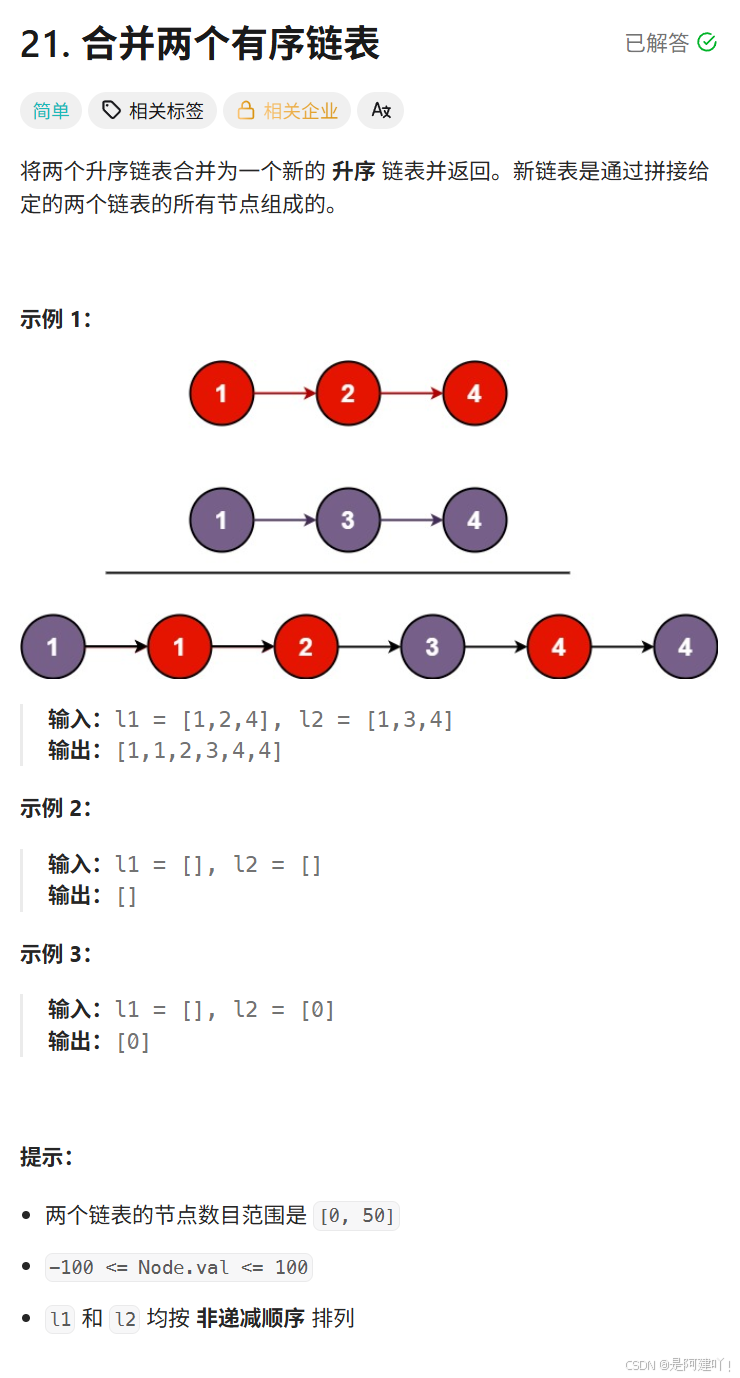
思路讲解:
本道题需要我们合并两条有序的链表,通过对比两个指针指向的节点,取出较小的一个节点,将剩余节点与另一条链表进行合并,问题又变成了合并两条有序的链表,所以本道题可以使用递归的方式完成。
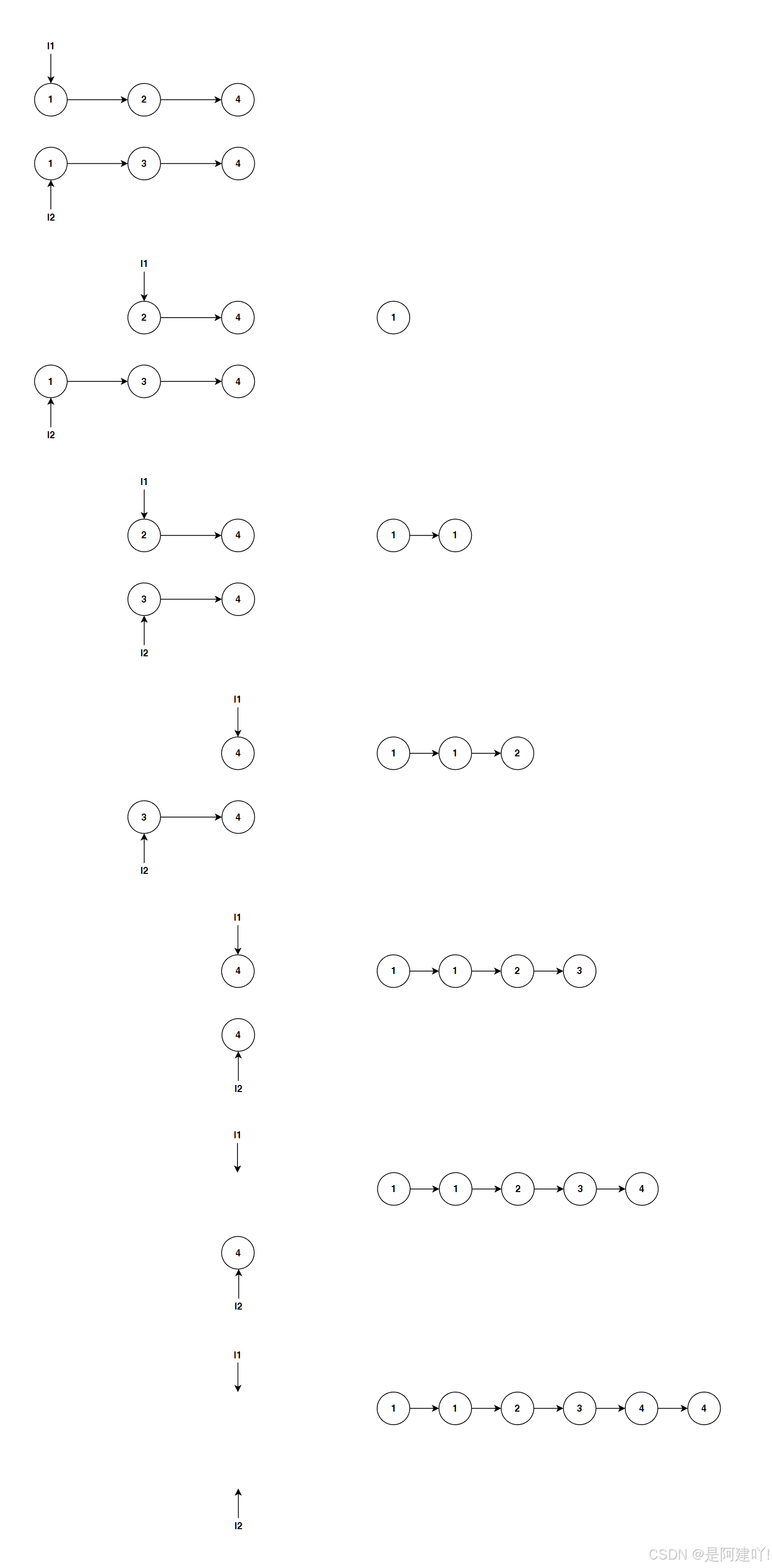
以下是具体思路:
- 终止条件:
- 当其中一个链表为空时,直接返回另一个链表(因为剩余节点已有序)
- 递归逻辑:
- 比较两个链表的当前头节点值,选择值较小的节点作为合并后链表的当前节点
- 对选中节点的下一个节点与另一个链表的当前节点进行递归合并,结果作为选中节点的next
- 返回选中的节点,作为当前层合并后的链表头
编写代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(!list1) return list2;if(!list2) return list1;ListNode* ret = nullptr;if(list1->val < list2->val){ret = list1;list1 = list1->next;}else{ret = list2;list2 = list2->next;}ret->next = mergeTwoLists(list1,list2);return ret;}
};
三、反转链表
题目描述:
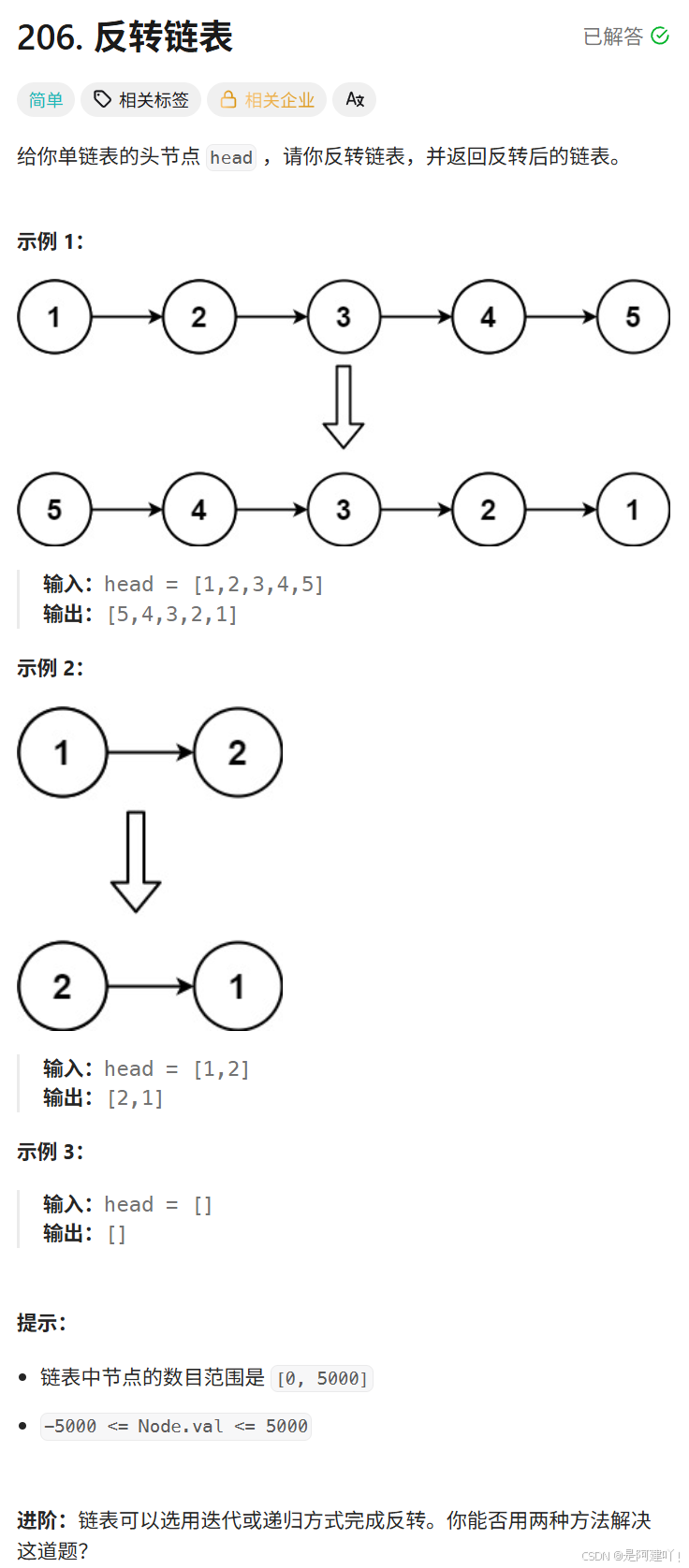
思路讲解:
本道题需要我们反转整个链表,首先我们可以想想是否可以先将前两个节点翻转,但是这样会导致第三个及后序节点丢失。
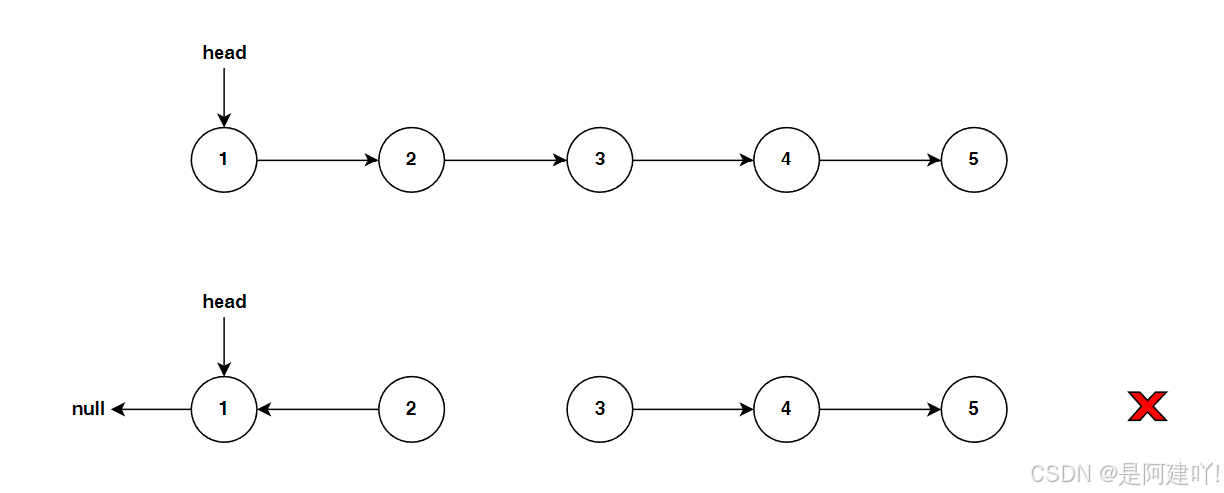
先将前两个节点翻转会导致后序节点丢失,所以我们先让后面的链表进行翻转,重复这个过程,直到最后一个节点,再层层返回向前进行链接,即可完成对整体链表的翻转。
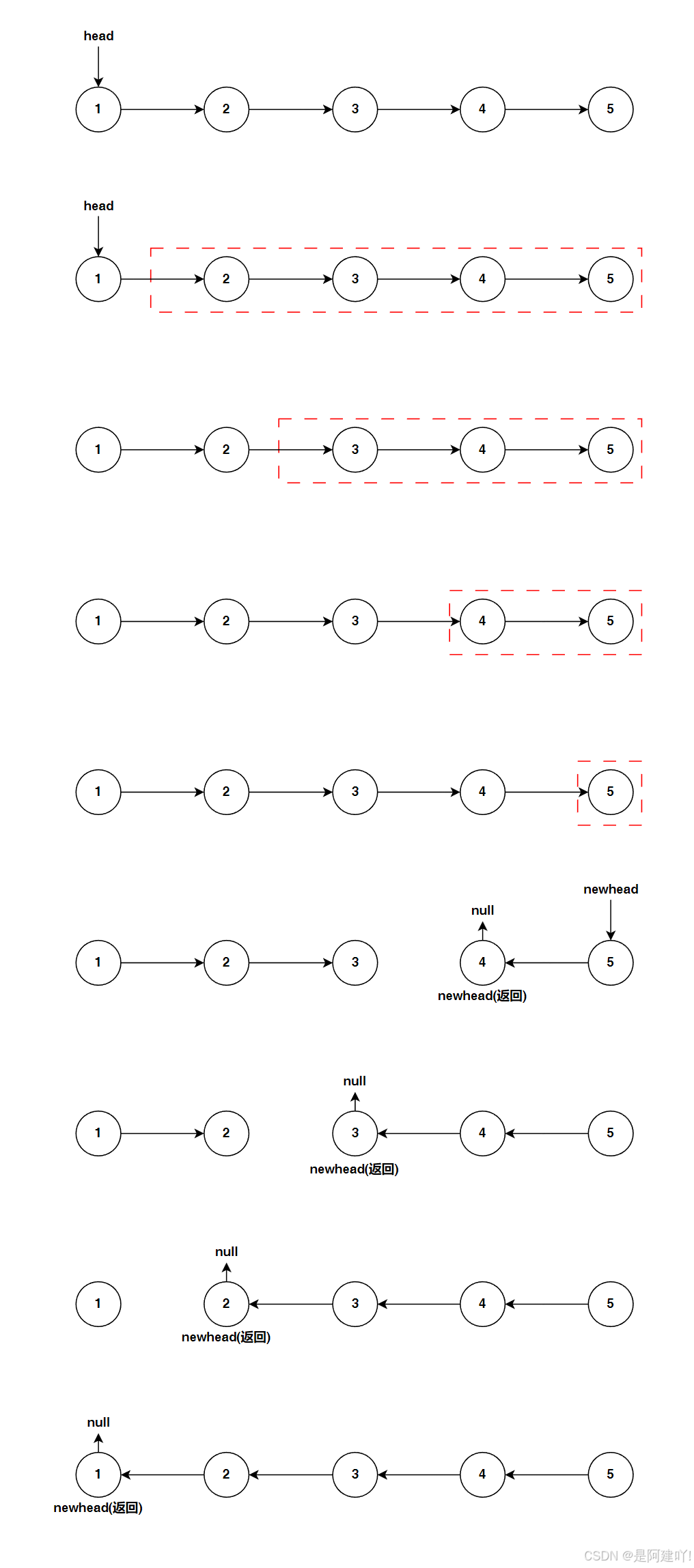
以下是具体思路:
- 终止条件:
- 当链表为空或只有一个节点时,无需反转,直接返回当前节点
- 递归逻辑:
- 找到链表的最后一个节点(新的头节点),这是递归的终止条件
- 在回溯过程中,将当前节点的下一个节点的 next 指向当前节点,完成局部反转
- 将当前节点的 next 设为 nullptr,避免形成环
编写代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if(!head || !(head->next))return head;ListNode* newhead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newhead;}
};
四、两两交换链表中的节点
题目描述:
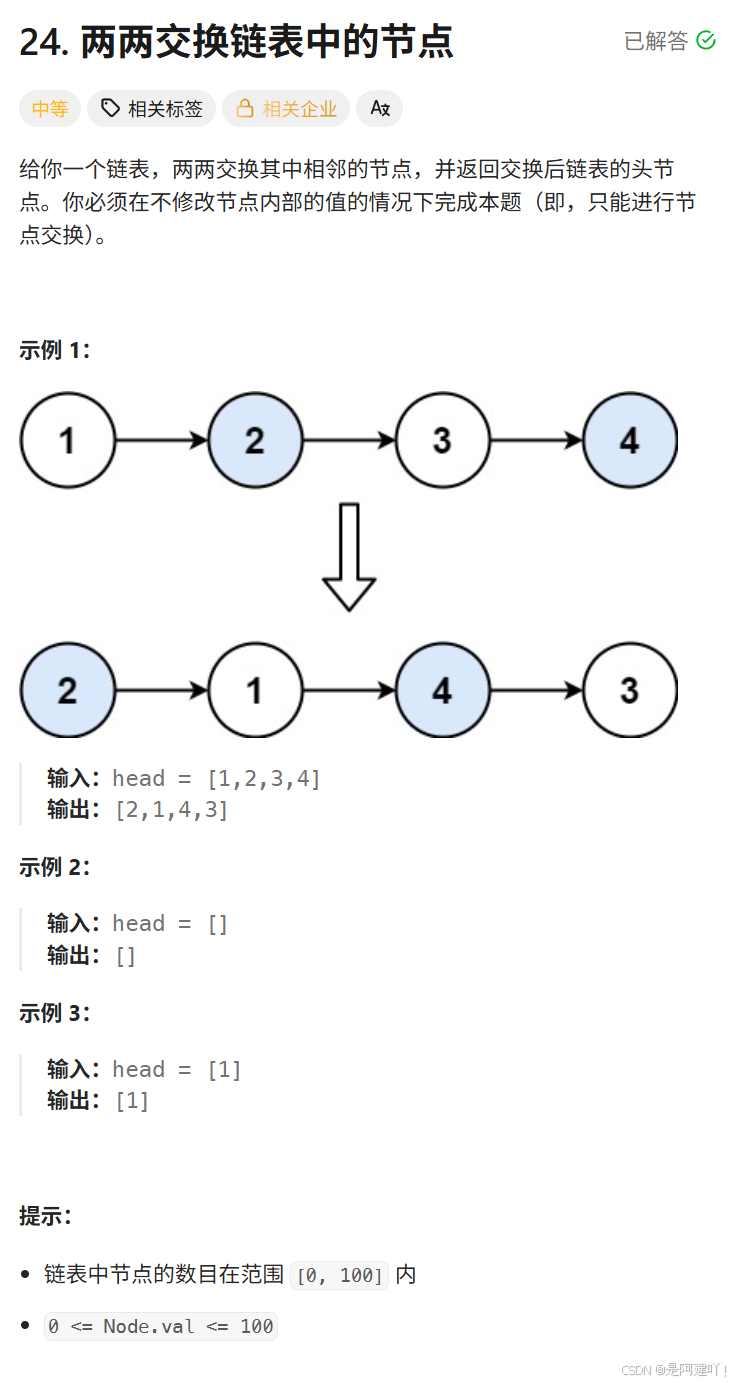
思路讲解:
本道题需要我们两两交换链表的节点,我们先让后面的链表进行两两交换,重复这个过程,直到最后一个节点或空节点,再层层返回,将该层的两个节点进行交换,然后向前进行链接,即可完成两两交换链表的节点。
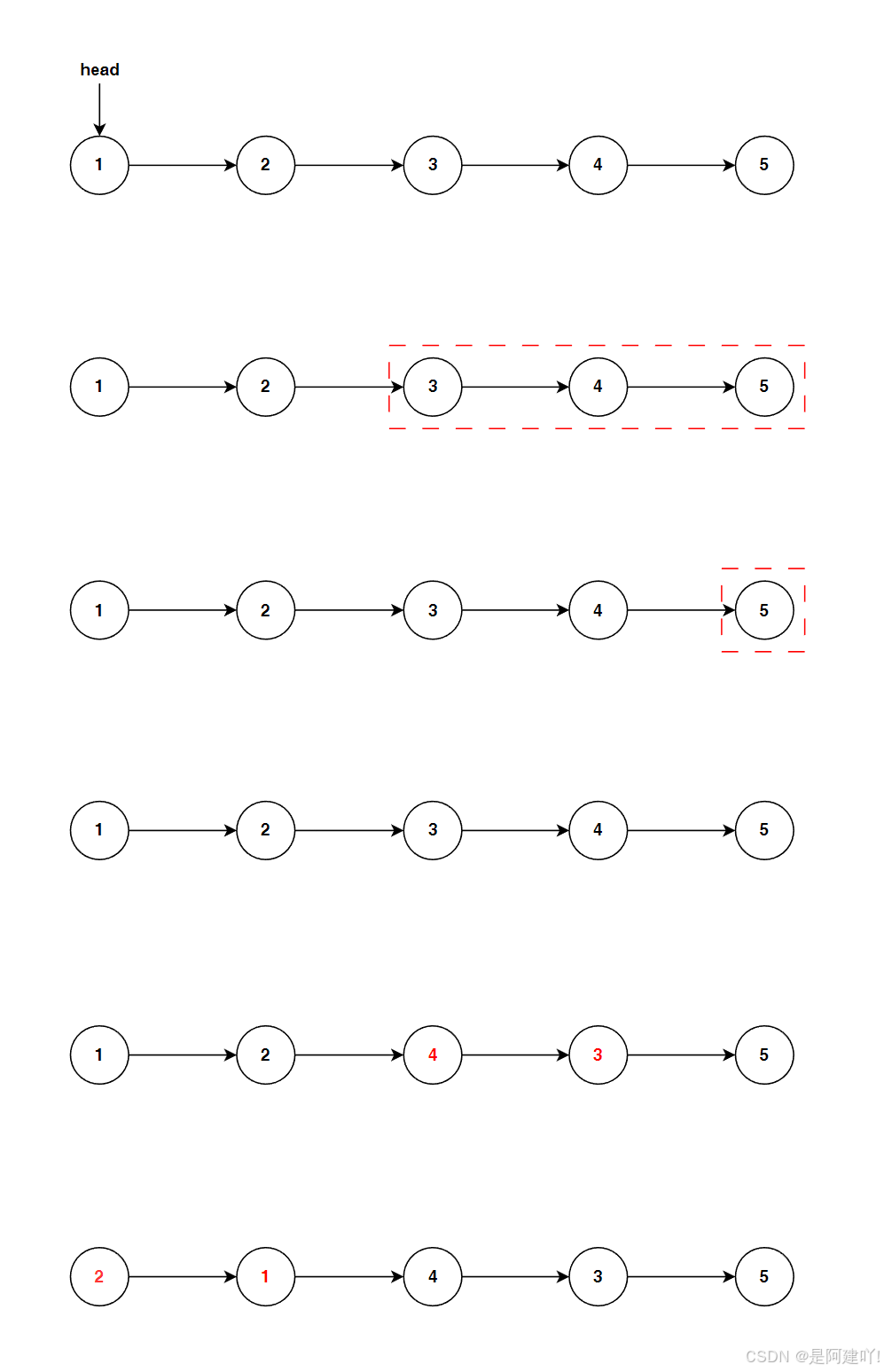
以下是具体思路:
- 终止条件:
- 当链表中剩余节点数不足 2 个时,无需交换,直接返回当前节点
- 递归处理后续节点:
- 先递归交换 head.next.next 及之后的所有节点,得到交换后的子链表头节点 newhead。这一步确保后续节点已经完成交换,为当前层的交换做好准备
- 交换当前层的两个节点:
- 记当前的两个节点为 first = head(第一个节点)和 second = head.next(第二个节点)
- 交换操作:second 的 next 指向 first(完成两个节点的互换)
- 连接后续链表:first 的 next 指向递归返回的 newHead(将当前交换后的节点与后续已交换的链表连接)
- 返回新头节点:
- 交换后,second 成为当前子链表的新头节点,返回 second 供上层递归使用
编写代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr)return head;ListNode* newhead = swapPairs(head->next->next);ListNode* ret = head->next;head->next->next = head;head->next = newhead;return ret;}
};
五、Pow(x, n)
题目描述:

思路讲解:
本道题想让我们计算 x 的整数 n 次幂函数,我们可以利用指数的二分特性:xnx^nxn = xn2x^{\frac{n}{2}}x2n *xn2x^{\frac{n}{2}}x2n(当 n 为偶数时),或 xnx^nxn = xn−12x^{\frac{n-1}{2}}x2n−1 * xn−12x^{\frac{n-1}{2}}x2n−1 * xxx(当 n 为奇数时)。通过递归将问题规模减半,避免逐次相乘的 O (n) 复杂度。以下是具体思路:
- 特殊条件:
- 当 n = 0 时,任何数的 0 次幂为 1
- 当 n < 0 时,xnx^nxn = 1/x−n1 / x^{-n}1/x−n,先计算正指数幂再取倒数
- 递归逻辑:
- 递归计算xn2x^{\frac{n}{2}}x2n 的结果(记为 tmp)
- 根据 n 的奇偶性,返回 tmp* tmp(偶数)或 tmp* tmp* x(奇数)
编写代码:
class Solution {
public:double myPow(double x, int n) {return n < 0 ? 1/pow(x,-(long long)n) : pow(x,n);}double pow(double x, long long n) {if(n == 0) return 1;if(n % 2 == 1){double tmp = pow(x,(n-1)/2);return tmp * tmp * x;}else{double tmp = pow(x,n/2);return tmp * tmp;}}
};
结尾
如果有什么建议和疑问,或是有什么错误,大家可以在评论区中提出。
希望大家以后也能和我一起进步!!🌹🌹
如果这篇文章对你有用的话,希望大家给一个三连支持一下!!🌹🌹

