向量空间模型
基本介绍
向量空间模型由(Vector Space Model,VSM)是由索尔顿几人于20世纪70年代提出的,并被成功地应用于著名的SMART文本检索系统,VSM将文本处理简化为向量空间中的向量运算,并通过向量相似度来表达语义上的相似度。
向量空间模型可以说是信息检索界跨时代的创举,改变布尔值模型说一不二的缺陷时,也实现了查重和检索的大一统。
模型构建
文档的词袋化
首先,从意群的角度来看,我们不需要了解文字的顺序了解意群,只需分出某些正确的词条,因此,索尔顿为了实现正确的分词和含义输出,首先定义了如下概念:
- 文档(Document):通常是文档中具有一定规模的片段,如句子、句群、段落、段落组或正篇文章。文档也称文本(Text)
- 词项(Term):词项是向量空间模型中最小的不可分的语言单元,可以是汉字、单词、词组或短语等。一个文档的内容被看成是它含有的词项所组成的集合,词项又经常被称为特征或特征项(Feature)
- 权重(Weight):对于文档的每一个词项,都依据一定的原则被赋予相应的权重,表示它们在文档中的重要性
一个文档可以用它包含的词项及其权重的集合来表示。在这个集合中,词项与词项之间的顺序关系被忽略,词项的位置信息丢失,我们把这个模型称为词袋模型。
文档的向量化
不同的文档长度不同,而查询结果往往却就是一个或几个单词,因此,我们也可以去掉文档的长度信息,也就是说可以把所有文档视为等长的,这种方法就叫向量化。
这里预先设定一个词典(Vocabulary),该词典包含了在所有文档中可能会出现的词项。既然在词袋化过程中已经去掉了词项的位置信息,那么对于一个文档,只需要表达表示词典中的任意词项是否在该文档中出现,或者出现了多少次就可以了。假设有一个由n个词项构成的词典V,对于一个长度为m的文档D,我们总是可以把D表示为一个n维的向量。向量维度恒为词典V的长度n,每一维的值为V中对应词项在文档中出现的频次或权重,向量的维数与文档D的长度m没有关系。
向量化过程如下:
| 文档编号 | 文档内容 | 词汇表(所有文档的去重词) | 词频统计(对应词汇表顺序) | 词袋向量(基于词频) |
|---|---|---|---|---|
| 文档 1 | “猫抓老鼠,老鼠怕猫” | [猫,抓,老鼠,怕,狗,追,鱼] | 猫:2 次,抓:1 次,老鼠:2 次,怕:1 次,狗:0 次,追:0 次,鱼:0 次 | [2, 1, 2, 1, 0, 0, 0] |
| 文档 2 | “狗追猫,猫躲狗” | 同上(词汇表统一) | 猫:2 次,抓:0 次,老鼠:0 次,怕:0 次,狗:2 次,追:1 次,鱼:0 次 | [2, 0, 0, 0, 2, 1, 0] |
| 文档 3 | “猫吃鱼,老鼠偷鱼” | 同上(词汇表统一) | 猫:1 次,抓:0 次,老鼠:1 次,怕:0 次,狗:0 次,追:0 次,鱼:2 次 | [1, 0, 1, 0, 0, 0, 2] |
词项的权重计算
布尔权重表示
如果词项在文档中出现,则将向量的对应维度置为1。这也是一种最简单的权重计算方法,当词项出现为1,否则为0。
频次权重表示
顾名思义,对应维度置为出现的频次(上例当中的方法)
停用词处理
在一些文档集合当中会出现一些“废话”,中文里有“啊、哦、额”,英文里有“a、an、the”这些词在文档当中出现的次数很多,可实际贡献很小,常见的处理方法是不管文档当中出现几次,都统计为1。
TF-IDF表示
这个模型在我早期的博客当中有所提及(TF-IDF)
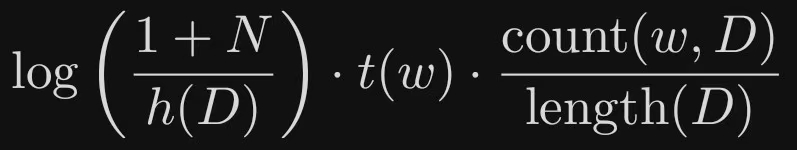
import mathdef tf_idf(count_w, length_D, N, sum_I):# 计算 TF 值,即词 w 在文档 D 中的词频tf = count_w / length_D# 计算 IDF 值,即逆文档频率idf = math.log((1 + N) / (1 + sum_I))# 计算 TF-IDF 值tf_idf_value = tf * idfreturn tf_idf_value
这个模型当中:
- count(w)表示词项w在当前文档D中出现的频次
- length(D)表示当前文档的长度(词数)
- N表示文档集合的大小
- I(w,D_i)=1表示词项w在第i个文档D_i中出现,否则为0
- +1用于表示平滑处理(解决除数为0的问题)
相似度计算
常用于衡量两个向量之间相似程度的方法是余弦相似度计算法,对于两个向量
X=[x_1,x_2,⋯,x_n]和Y=[y_1,y_2,⋯,y_n],其计算公式为:
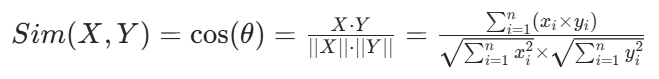
其中,
- n为向量的维度(在文本相关场景中可理解为词典的大小)
- x_i为向量X中第i个元素的值(在文本中可表示词典中第i个词项在文档X中的权重)
- y_i为向量Y中第i个元素的值(同理对应文档Y)
- θ为向量X和向量Y的夹角
