硅基计划3.0 学习总结 肆 二叉树 初版

---

---

一、树与性质

1. 二叉树初识

二叉树指的是不存在>=2度数（子节点个数）的节点，分为左右子树，但是二叉树也有可能是空树

• 完全二叉树：节点编号和节点一一对应，而且如果节点度数是偶数，不存在度为1的节点，如果是偶数，则一定存在一个度为1的节点，如下图所示
  

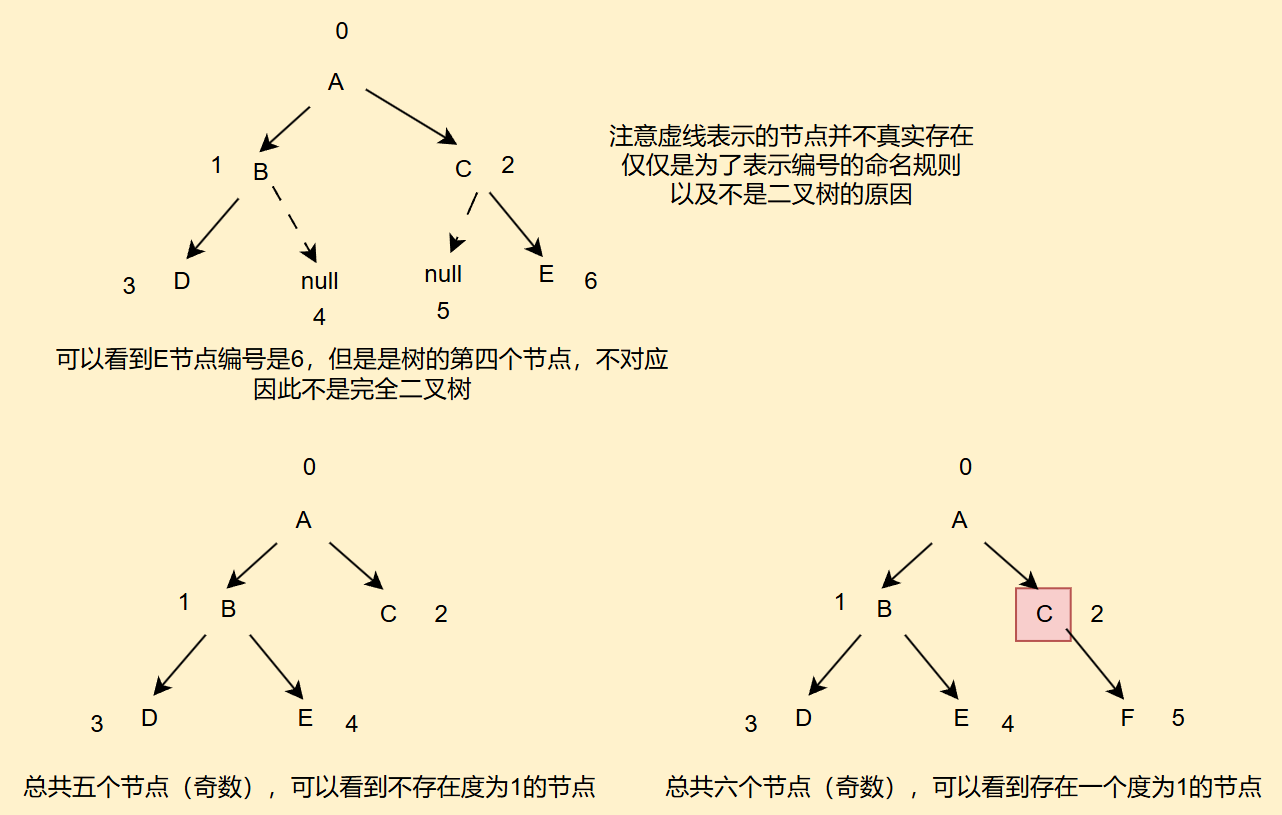
• 满二叉树：每个节点除了最后一层以外的节点度数都为2，起始就是完全二叉树的特殊情况

2. 树的表示

树可以有多种表示方法，有双亲表示、孩子表示、孩子兄弟等，对于树的定义不过多细讲了

class Node{int value;Node firstChild;Node NextBrother;
}

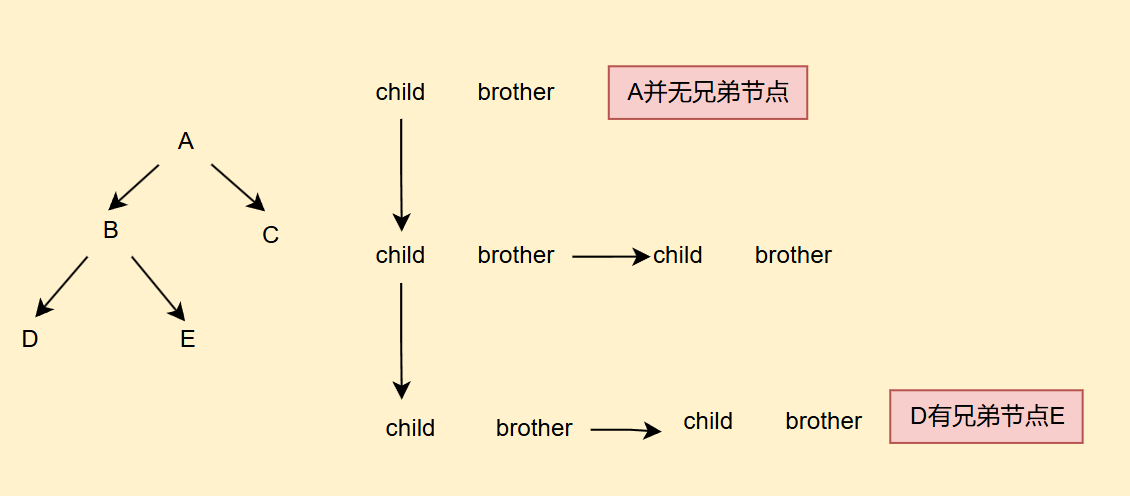
3. 二叉树性质

1. 如果规定第一层的层数下标是一（意思就是不是用数组那种从零下标开始的叫法），那么第L层的最多有$2^k-1$个节点
2. 如果规定第一层的深度下标是一，那么深度为K的树节点总共有$2^k-1$个节点
3. 度为1的节点总比度为0的节点少一个

度数之和是度数为0的节点之和+度为1的节点之和+度为2的节点之和
而且边数比节点数少一个，利用这个性质，我们可以得到这个推论

4. 具有n个节点的完全二叉树的深度为${\log }_2(n+1)$，结果向上取整（比如5.2–>6，5.8–>6）
5. 含有n个节点的完全二叉树，如果i=0，那么它就是根节点，否则如果下标i>0，那么它的双亲下标就是(i-1)/2；同理如果2i+1<n，它的左子树（左孩子）下标是2i+1，否则不存在；同理如果2i+2>n，它的右子树（右孩子）下标是2i+2，否则不存在
   

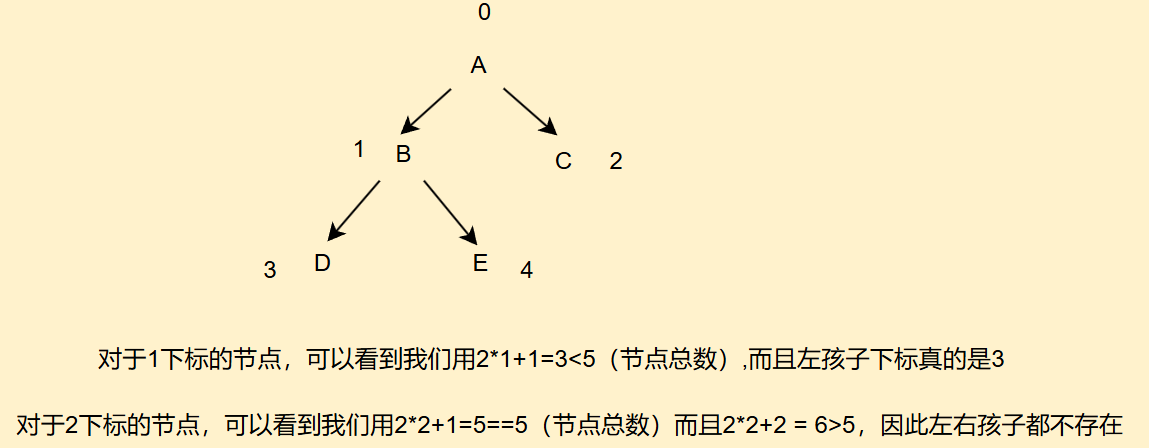
二、模拟实现二叉树

二叉树的表示常用的是孩子表示法（一个节点的左右两个子节点）和孩子双亲表示法（除了左右两个子节点还包括自己）
接下来我们模拟实现最常用的孩子表示法

1. 创建二叉树

public class BinaryTree {static class TreeNode{int value;TreeNode left;//左孩子TreeNode right;//右孩子public TreeNode(int value) {this.value = value;}}public TreeNode creatNode(){TreeNode t1 = new TreeNode(15);TreeNode t2 = new TreeNode(22);TreeNode t3 = new TreeNode(34);TreeNode t4 = new TreeNode(56);TreeNode t5 = new TreeNode(77);TreeNode t6 = new TreeNode(99);//手动连接//左子树t1.left = t2;t1.right = t3;t2.left = t4;t2.right = t5;//右子树t3.left = t6;//返回头节点return t1;}//一些操作方法
}//测试类中
public class Test {BinaryTree binaryTree = new BinaryTree();BinaryTree.TreeNode root = binaryTree.creatNode();
}

2.遍历

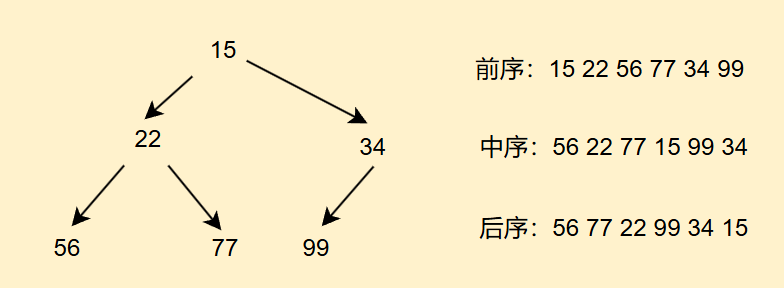
分为前序——根节点左孩子节点右孩子节点，中序——左跟右，后序——左右根，区别只是遍历的顺序不一样，他们的时间空间复杂度都是O(n)

    //前序遍历public void preOrder(TreeNode root){if(root == null){return;}System.out.print(root.value+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(TreeNode root){if(root == null){return;}inOrder(root.left);System.out.print(root.value+" ");inOrder(root.right);}//后序遍历public void pastOrder(TreeNode root){if(root == null){return;}pastOrder(root.left);pastOrder(root.right);System.out.print((root.value + " "));}//测试//前序遍历binaryTree.preOrder(root);System.out.println();//中序遍历binaryTree.inOrder(root);//后序遍历System.out.println();binaryTree.pastOrder(root);

这里我就拿前序遍历举例子

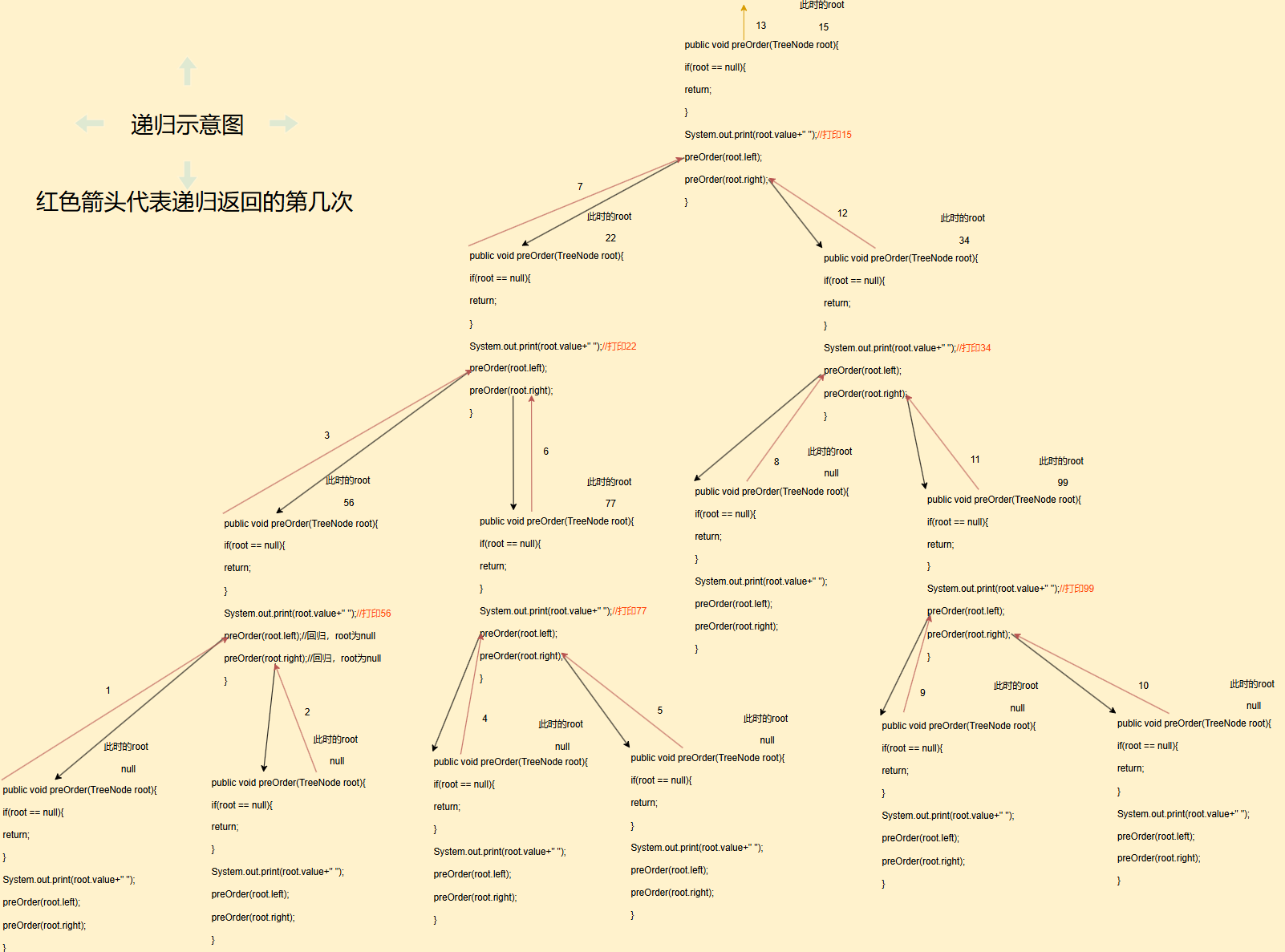
3. 求节点个数

我们思路就是利用计数器，或者是子问题思路——左子树节点个数+有子树节点个数，他们的时间空间复杂度都是O(n)

ublic int count = 0;//计数器法则public void size(TreeNode root){if(root == null){return;}count++;size(root.left);size(root.right);}//子问题法则public int sizePlus(TreeNode root){if(root == null){return 0;}return sizePlus(root.left)+sizePlus(root.right)+1;}

4. 求叶子节点

我们的思路就是如果遇到了叶子节点就++，即当前节点的左右孩子节点都是空，时间空间复杂度都是O(n)

public int getLeafNodeCount(TreeNode root){if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return getLeafNodeCount(root.left)+getLeafNodeCount(root.right);}

5. 求第K层节点个数

我们思路就是第K层是左子树的K-1层+右子树的K-1层
我们让K一直减减，直到K=1的时候，时间空间复杂度都是O(n)

//求第K层节点个数public int getLevelCount(TreeNode root,int k){if(root == null){return 0;}if(k == 1){return 1;}return getLevelCount(root.left,k-1)+getLevelCount(root.right,k-1);}

6. 获取二叉树的高度（深度）

我们思路就是左右两个子树求出深度，谁的值比较大就取谁，最后再加上一（根节点），时间复杂度是O(n)，空间复杂度是O(logN)

//求二叉树深度public int getHeight(TreeNode root){if(root == null){return 0;}return Math.max(getHeight(root.left),getHeight(root.right))+1;}

7. 检测指定值是否存在于二叉树中

我们的思路就是先判断根节点是不是我们要找的值，不是就递归，如果左子树没有，就去判断右子树，时间复杂度O(n)，空间复杂度O(logN)

//检测值是否存在public TreeNode find(TreeNode root,int value){if(root == null){//终止情况return null;}if(root.value == value){//检测根节点情况return root;}TreeNode ret = find(root.left,value);//检查左子树if(ret != null){return ret;//找到了直接返回，下面语句不用进行了}ret = find(root.right,value);//左子树找不到，找右子树if(ret != null){return ret;//找到了直接返回}return null;//找不到语句到这里}

---

文章错误不可避免，期待您的指正，我们共同进步

---

---

END