剑指offer第2版：双指针+排序+分治+滑动窗口

一、p129-JZ21使奇数位于偶数前面（不考虑相对位置）（hoare快排双指针）

调整数组顺序使奇数位于偶数前面(二)_牛客题霸_牛客网

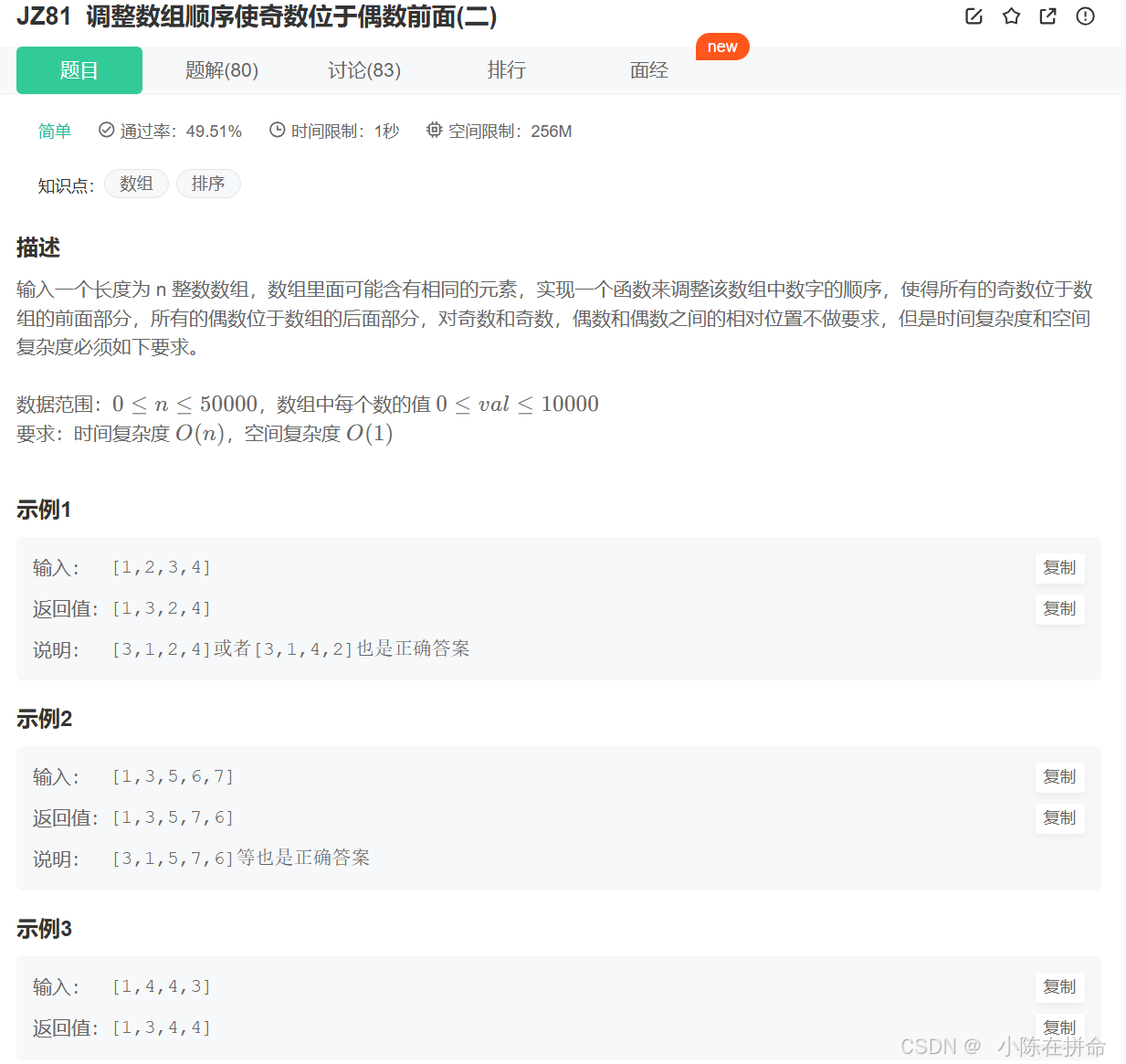
         如果不考虑相对位置的话，那么我们可以模仿hoare快排，使用双指针的思想，一个指针在前向后找偶数，一个指针在后，向前找奇数，然后再交换就行 时间复杂度是n 

class Solution {public:vector<int> reOrderArrayTwo(vector<int>& nums) {//用双指针int n = nums.size();if (n == 0) return{};int left = 0, right = n - 1;//左边找偶数，右边找奇数 然后交换while (left < right) {while (left < right && nums[left] & 1) ++left;while (left < right && (nums[right] & 1) == 0) --right;if (left < right) swap(nums[left], nums[right]);}return nums;}
};

二、p129-JZ21使奇数位于偶数前面（考虑相对位置）（插入排序）

调整数组顺序使奇数位于偶数前面(一)_牛客题霸_牛客网

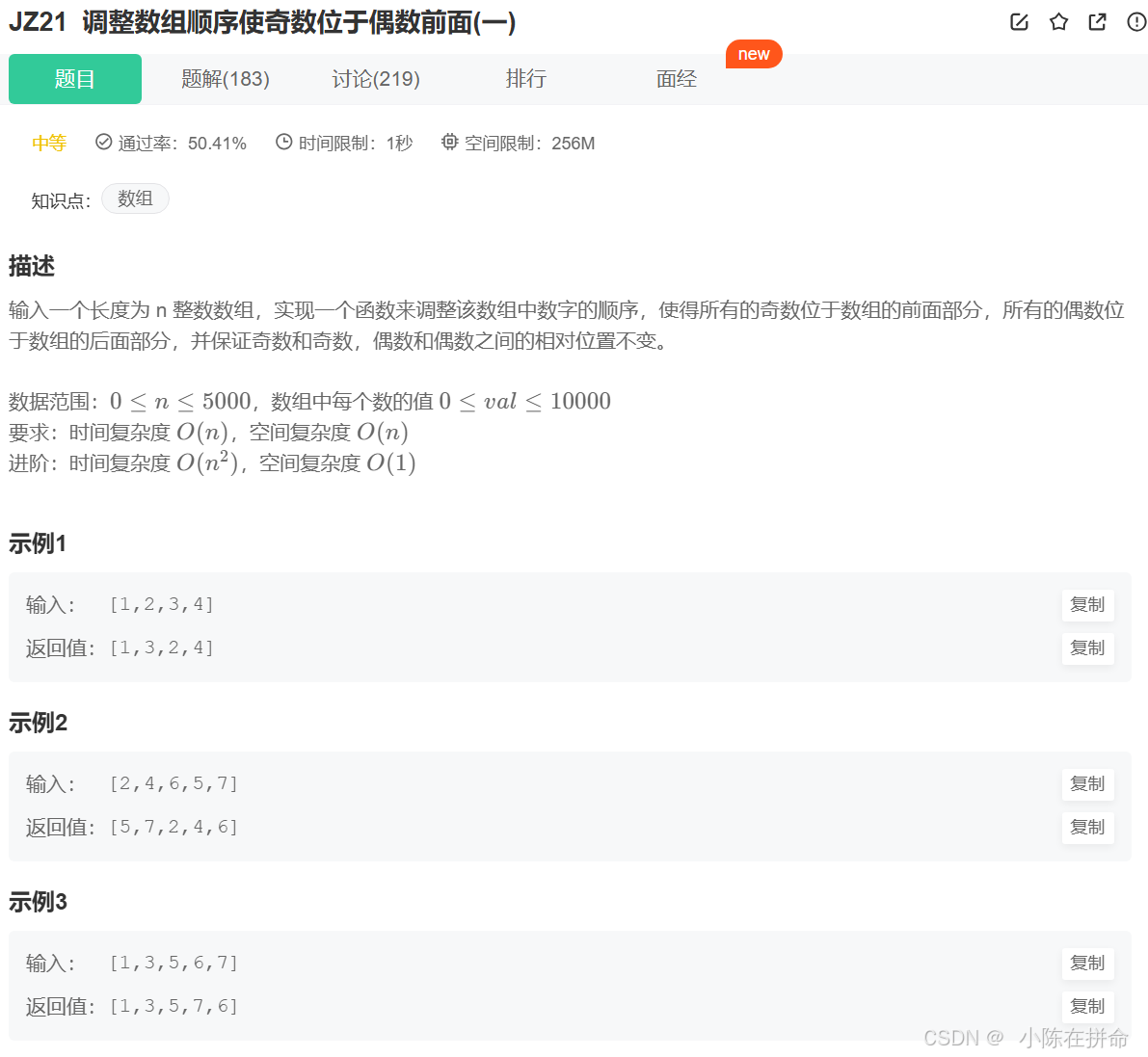
因为要考虑相对位置，所以我们就要借鉴一下插入排序的思想 

class Solution {public:vector<int> reOrderArray(vector<int>& nums) {//奇数位于偶数前面，并且还要保证相对位置不变//那就得用到插入排序的思想了！ //从前往后 看到奇数我就想办法往前挪//1 3 5 6 7int n = nums.size();int k = 0;for (int i = 0; i < n; ++i)if (nums[i] &1) { //从左向右，每次遇到的，都是最前面的奇数，一定将来要被放在k下标处int temp = nums[i]; //先将当前奇数保存起来int j = i;while (j >  k) { //将该奇数之前的内容(偶数序列)，整体后移一个位置nums[j] = nums[j - 1];--j;}//将奇数保存在它将来改在的位置，因为我们是从左往右放的，没有跨越奇数，所以一定是相对位置不变的nums[k++] =temp; }return nums;}
};

  扩展：如果面试官问你如果想要把题目改成将负数放在非负数前面，或者将可以被3整除的放在不能被3整除的数的前面，这个时候我们可以通过传入仿函数来设计一套通用的解法，然后只需要在判断的逻辑那里调用仿函数可以。这样可以实现解耦成两部分：一是判断数字应该在数组的前半部分还是后半部分的标准，而是拆分数组的操作。

三、p249-JZ51数组中的逆序对（归并排序）

数组中的逆序对_牛客题霸_牛客网

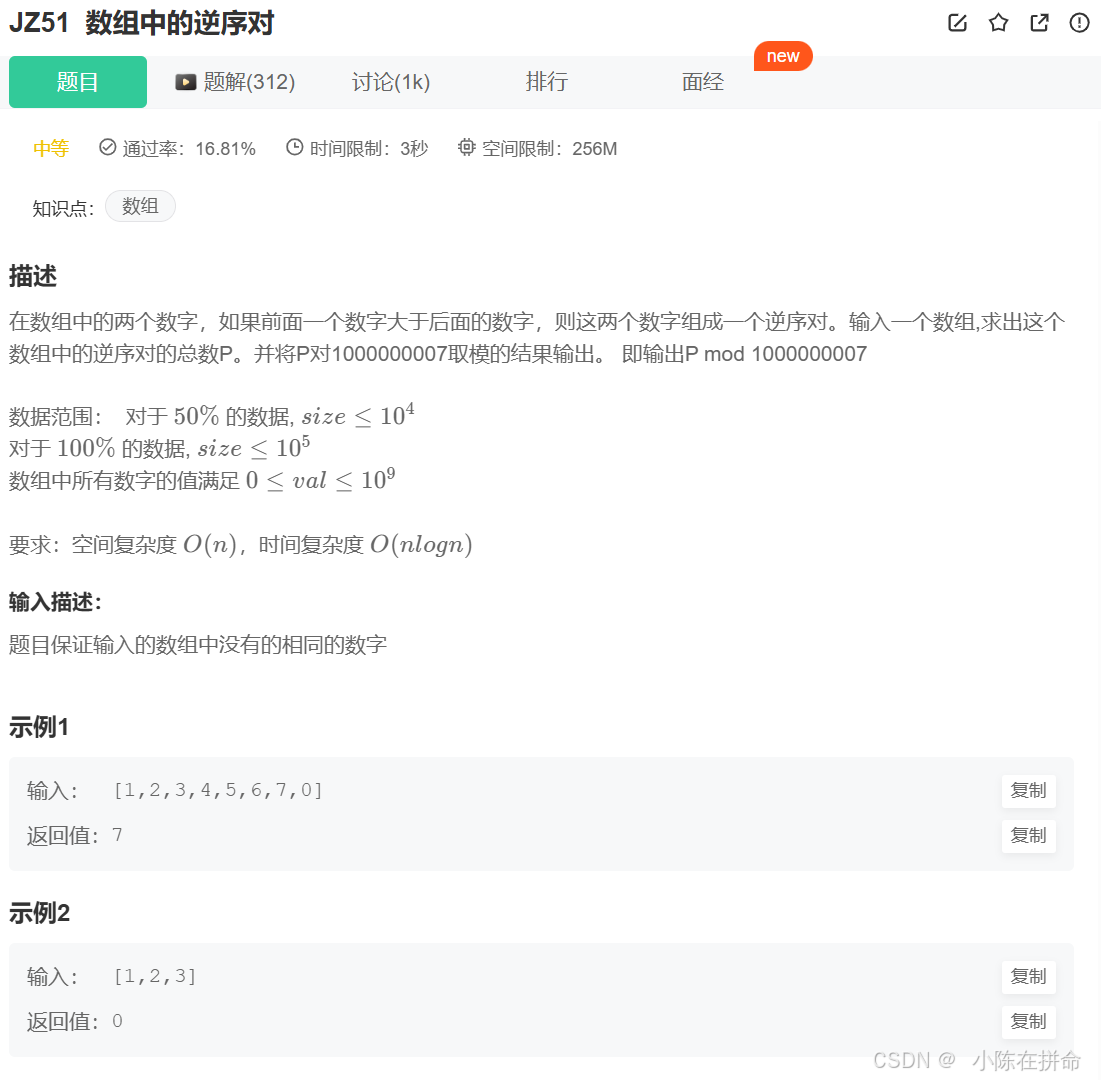
    该题能够使用归并排序，本质是利用了待合并有序数组的单调性，我们在题目中需要去找到区间前的数和区间后的数存在某种大小关系的时候，我们就可以用分治思想中的归并排序在两段待排序的升序区间中根据单调性去找我们想要的结果。

升序的做法： 以后面区间为基点，找前面区间有多少数字比我大

class Solution {
public:
//升序 以l2为基准 找前面有多少数字比我大const int MOD=1e9+7;int InversePairs(vector<int>& nums) {int n=nums.size();vector<int> temp(n);return mergesort(nums,0,n-1,temp);}int mergesort(vector<int>& nums,int begin,int end,vector<int>& temp){if(begin>=end) return 0;int mid=(begin+end)>>1;int ret=mergesort(nums,begin,mid,temp)+mergesort(nums,mid+1,end,temp);int cur1=begin,cur2=mid+1,i=begin;while(cur1<=mid&&cur2<=end)if(nums[cur1]<=nums[cur2]) temp[i++]=nums[cur1++];else{ret+=mid-cur1+1;ret%=MOD;temp[i++]=nums[cur2++];}while(cur1<=mid) temp[i++]=nums[cur1++];while(cur2<=end) temp[i++]=nums[cur2++];//开始还原for(i=begin;i<=end;++i) nums[i]=temp[i];return ret;}
};

降序的做法： 以前面区间为基点，找后面区间有多少数字比我小

class Solution {
public:
//降序 以l1为基准 找后面有多少数字比我小const int MOD=1e9+7;int InversePairs(vector<int>& nums) {int n=nums.size();vector<int> temp(n);return mergesort(nums,0,n-1,temp);}int mergesort(vector<int>& nums,int begin,int end,vector<int>& temp){if(begin>=end) return 0;int mid=(begin+end)>>1;int ret=mergesort(nums,begin,mid,temp)+mergesort(nums,mid+1,end,temp);int cur1=begin,cur2=mid+1,i=begin;while(cur1<=mid&&cur2<=end)if(nums[cur1]<=nums[cur2]) temp[i++]=nums[cur2++];else{ret+=end-cur2+1;ret%=MOD;temp[i++]=nums[cur1++];}while(cur1<=mid) temp[i++]=nums[cur1++];while(cur2<=end) temp[i++]=nums[cur2++];//开始还原for(i=begin;i<=end;++i) nums[i]=temp[i];return ret;}
};

 四、p209-JZ40最小的k个数（快速选择排序）

最小的K个数_牛客题霸_牛客网

方法1：建大堆 一个个和堆顶比较，最后剩下的k个数要找的（适合处理海量数据）

#include <queue>
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int>& input, int k) {int n=input.size();if(k==0||n==0||k>n) return {};//搞一个大根堆  然后让前k个进去  然后再一个个排除 最后剩下的就是最小的k个数priority_queue<int> q;for(int i=0;i<k;++i) q.push(input[i]);//前k个丢进去//然后开始排除for(int i=k;i<n;++i) if(input[i]<q.top()){q.pop();q.push(input[i]);}//插入到数组中返回vector<int> ret(k);for(int i=0;i<k;++i){ret[i]=q.top();q.pop();}return ret;}
};

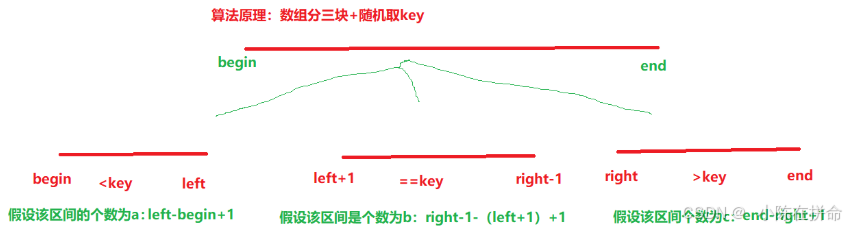
方法2：快速选择排序算法（适合单次查找且可以修改原数组的情况下）

#include <cstdlib>
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int>& nums, int k) {srand((unsigned int)time(nullptr));//时间种子qsort(nums,0,nums.size()-1,k);return {nums.begin(),nums.begin()+k};}void qsort(vector<int>& nums,int begin,int end,int k){if(begin>=end) return;//要按照数组分三块的思想int key=nums[rand()%(end-begin+1)+begin];int left=begin-1,right=end+1,cur=begin;while(cur<right)if(nums[cur]<key) swap(nums[cur++],nums[++left]);else if(nums[cur]>key) swap(nums[--right],nums[cur]);else ++cur;//根据区间大小进行选择int a=left-begin+1,b=(right-1)-(left+1)+1;if(k<a) qsort(nums,begin,left,k);//说明在左边区间里 继续排序else if(k<=a+b) return;else qsort(nums,right,end,k-a-b);//说明在第三块区间里}
};

五、p214-JZ41数据流中的中位数（优先级队列）

数据流中的中位数_牛客题霸_牛客网

策略：优先级队列大小堆维护中位数   add(logN)  find(1)

设计思路：

1、建立left为大根堆，right为小根堆

2、我们的add控制始终保持left的数量要么和right相等，要么比right多一个，为了能够满足在O（1）的复杂度内完成找到中位数的任务，我们希望当left多一个的时候，left堆顶的元素就是中位数，而当left和right相等的时候，中位数就是两个堆的堆顶元素的平均值。

3、为了达到这个目的，我们在时刻控制left和right的数量的同时，一定要保证left里面的元素是小于等于right里面的元素的，所以add要分两种情况去讨论：

情况1：当两个堆的元素个数相等的时候

    （1）如果left为空，或者是add的元素比left的堆顶元素小，那么就让该元素直接进left

    （2）如果add的元素比left的堆顶元素大，那么他也有可能会比right的元素大，所以我们必须要将这个元素丢到right中，但是直接丢就会破坏规则，所以我们要先将add的元素丢到right中进行调整，然后再将right的堆顶元素丢到left中去，保持left和right的数量关系。 （注意，这里的先后顺序很重要，我们不能先将right的堆顶元素丢到left中，然后再将add丢到right中进行调整，因为我们只是知道这个数比left的堆顶元素大，但是他是比right的堆顶元素大还是小我们不得而知，必须要通过他自己的向下调整去选出来）

情况2：当left的元素比right多一个的时候

  （1）如果add的元素比left的堆顶元素大，这个时候无脑进右边就行了。

   （2）如果add的元素比left的堆顶元素小，这个时候我们也得把add的元素丢到left中，然后为了保持数量关系，将调整过后的left的堆顶元素移到right中即可。

细节处理：

1、我们在比较的时候始终实用left的元素进行比较，因为左边不为空的时候右边也可能为空，所以我们如果不用left去比较而是用right去比较，那么还需要多考虑一种边界情况。

2、虽然我们add的都是int类型，但是当两个堆的元素个数相同的时候，我们去取两个堆顶元素取平均值的，而平均值是有可能会出现小数的，所以如果我们还用int的话可能会造成小数点丢失，所以我们在/2的时候变成/2.0,这样结果就会被强转成double；

class Solution {
public:void Insert(int num) {//如果为空 直接插入左边//如果两边一样多,  若<=left 直接插左边 若>right 就先插入右边 然后再移堆顶int m=left.size(),n=right.size();if(m==n)if(left.empty()||num<=left.top()) left.push(num);else{//num>left>left.topright.push(num);left.push(right.top());right.pop();} //如果左边比右边多  else{//m==n+1if(num>left.top()) right.push(num);else{//num<=left.topleft.push(num);right.push(left.top());left.pop();}}}double GetMedian() { //如果左边比右边多 就返回左边     如果相等就返回中间值if(left.size()>right.size()) return left.top();else return (left.top()+right.top())/2.0;}
private://需要有一个大根堆(在前面) 一个小根堆(在后面)priority_queue<int> left;//大根堆priority_queue<int,vector<int>,greater<int>> right;///右边是小根堆
};

六、p227-JZ45把数组排成最小的数（重写排序/冒泡排序）

把数组排成最小的数_牛客题霸_牛客网

方法一：重载比较的排序（推荐使用）

具体做法：

• step 1：优先判断空数组的特殊情况。
• step 2：将数组中的数字元素转换成字符串类型。
• step 3：重载排序比较为字符串类型的x + y < y + x，然后进行排序。
• step 4：将排序结果再按照字符串拼接成一个整体。

class Solution {
public:string PrintMinNumber(vector<int>& nums) {int n=nums.size();if(n==0) return"";vector<string> strs;strs.reserve(n);for(auto&num:nums) strs.emplace_back(to_string(num));sort(strs.begin(),strs.end(),[&strs](const string&s1,const string&s2){return s1+s2<s2+s1;});string ret;for(auto&s:strs) ret+=s;return ret;}
};

方法二：冒泡排序（扩展思路）

class Solution {
public:string PrintMinNumber(vector<int> numbers) {string res = "";//空数组的情况if(numbers.size() == 0)return res;vector<string> nums;//将数字转成字符for(int i = 0; i < numbers.size(); i++)nums.push_back(to_string(numbers[i]));//冒泡排序for(int i = 0; i < nums.size() - 1; i++){for(int j = 0; j < nums.size() - i - 1; j++){string s1 = nums[j] + nums[j + 1];string s2 = nums[j + 1] + nums[j];//比较拼接的大小交换位置if(s1 > s2) swap(nums[j], nums[j + 1]);}}//字符串叠加for(int i = 0; i < nums.size(); i++)res += nums[i];return res;}
};

七、p280-JZ57和为S的两个数字（双指针+单调性）

和为S的两个数字_牛客题霸_牛客网

思路：

我们能想到最直观的解法，可能就是两层遍历，将数组所有的二元组合枚举一遍，看看是否是和为目标值，但是这样太费时间了，既然加法这么复杂，我们是不是可以尝试一下减法：对于数组中出现的一个数a，如果目标值减去a的值已经出现过了，那这不就是我们要找的一对元组吗？这种时候，快速找到已经出现过的某个值，可以考虑使用哈希表快速检验某个元素是否出现过这一功能。

具体做法：

• step 1：构建一个哈希表，其中key值为遍历数组过程中出现过的值
• step 2：遍历数组每个元素，如果目标值减去该元素的结果在哈希表中存在，说明我们先前遍历的时候它出现过，根据保存的值，就可以得到结果。
• step 3：如果相减后的结果没有在哈希表中，说明先前遍历的元素中没有它对应的另一个值，那我们将它加入哈希表，等待后续它匹配的那个值出现即可。

class Solution {
public:vector<int> FindNumbersWithSum(vector<int> nums,int sum) {unordered_set<int> hash; //在哈希表中查找sum-array[i]for(auto&e:nums){int temp=sum-e;if(hash.find(temp)==hash.end()) hash.insert(e);else return {temp,e};}return {};}
};

思路：

这道题目还有一个条件是数组是升序序列，在方法一中没有用到。这个条件有什么用？既然数组是有序的，那我们肯定知道和找到一定程度就不找了，我们为什么要从最小的两个数开始相加呢？我们可以用二分法的思路，从中间开始找。

使用双指针指向数组第一个元素和最后一个元素，然后双指针对撞移动，如果两个指针下的和正好等于目标值sum，那我们肯定找到了，如果和小于sum，说明我们需要找到更大的，那只能增加左边的元素，如果和大于sum，说明我们需要找更小的，只能减小右边的元素。

具体做法：

• step 1：准备左右双指针分别指向数组首尾元素。
• step 2：如果两个指针下的和正好等于目标值sum，则找到了所求的两个元素。
• step 3：如果两个指针下的和大于目标值sum，右指针左移；如果两个指针下的和小于目标值sum，左指针右移。
• step 4：当两指针对撞时，还没有找到，就是数组没有。

class Solution {
public:vector<int> FindNumbersWithSum(vector<int> nums,int sum) {//双指针int left=0,right=nums.size()-1;while(left<right){int x=nums[left]+nums[right];if(x<sum) ++left;else if(x==sum) return{nums[left],nums[right]};else --right;}return {};}
};

八、扩展p282-JZ57 和为S的连续正数序列（滑动窗口）

 和为S的连续正数序列_牛客题霸_牛客网

思路：

从某一个数字开始的连续序列和等于目标数如果有，只能有一个，于是我们可以用这个性质来使区间滑动。

两个指针l、r指向区间首和区间尾，公式(l+r)∗(r−l+1)/2(l+r)∗(r−l+1)/2计算区间内部的序列和，如果这个和刚好等于目标数，说明以该区间首开始的序列找到了，记录下区间内的序列，同时以左边开始的起点就没有序列了，于是左区间收缩；如果区间和大于目标数，说明该区间过长需要收缩，只能收缩左边；如果该区间和小于目标数，说明该区间过短需要扩大，只能向右扩大，移动区间尾。

具体做法：

• step 1：从区间[1,2][1,2]开始找连续子序列。
• step 2：每次用公式计算区间内的和，若是等于目标数，则记录下该区间的所有数字，为一种序列，同时左区间指针向右。
• step 3：若是区间内的序列和小于目标数，只能右区间扩展，若是区间内的序列和大于目标数，只能左区间收缩。

class Solution {
public:vector<vector<int>> FindContinuousSequence(int n) {//滑动窗口if(n<3) return {};vector<vector<int>> ret;//结果集vector<int> path;//存储结果for(int left=1,right=2,total=3;left<right;total-=left,++left){while(total<n){++right;total+=right;}if(total==n){for(int i=left;i<=right;++i)  path.emplace_back(i);ret.emplace_back(path);path.clear();//清空}}return ret;}
};