【AcWing 838题解】堆排序

AcWing 838. 堆排序
【题目描述】

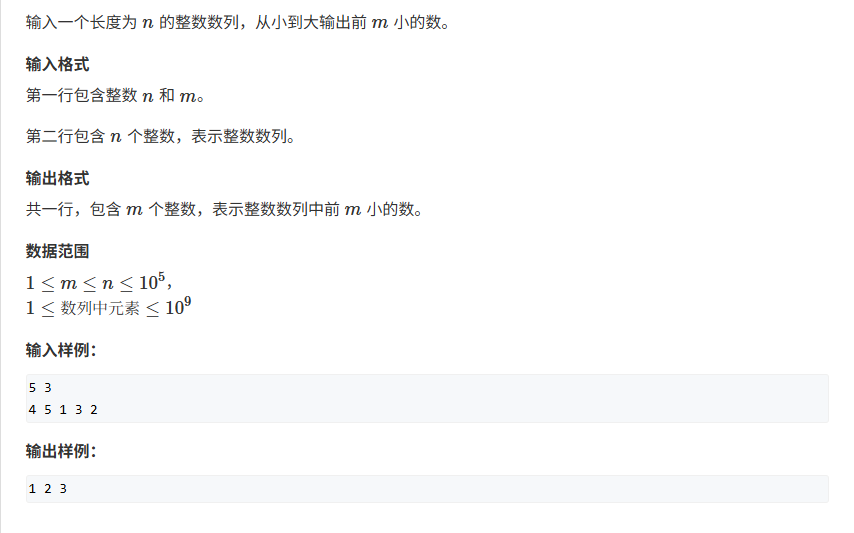
在查看解析之前，先给自己一点时间思考哦！

【题解】
该问题可以通过堆数据结构来解决。堆是一种完全二叉树，它支持：
插入操作：将一个元素加入堆中，并保持堆的性质。
删除操作：删除堆顶元素，并重新调整堆结构。

在本题中，我们需要反复取出最小的元素，并将剩余元素调整为有效的堆，因此可以使用小根堆。
【参考代码】

#include <iostream>
#include <algorithm>
using namespace std;const int N = 1e5 + 10;int h[N], cnt;  // h 存储堆，cnt 表示堆中元素的个数
int n, m;  // n 为元素个数，m 为需要输出的最小数的个数// down 函数：将堆中某个节点向下调整，保持最小堆的性质
void down(int u) {int t = u;  // 当前节点 t 为 uif(2 * u <= cnt && h[2 * u] < h[t])  // 如果左子节点存在，并且比当前节点小t = 2 * u;if(2 * u + 1 <= cnt && h[2 * u + 1] < h[t])  // 如果右子节点存在，并且比当前节点小t = 2 * u + 1;if(u != t) {  // 如果 t 发生了变化，说明需要交换swap(h[u], h[t]);  // 交换当前节点和子节点down(t);  // 递归继续调整交换后的子树}
}int main() {cin >> n >> m;  for(int i = 1; i <= n; i++)  cin >> h[i];cnt = n;  // 堆中的元素个数// 从最后一个非叶子节点开始，调整堆for(int i = n / 2; i; i--)  down(i);while(m--) {cout << h[1] << " ";  // 输出堆顶元素，即当前最小的元素h[1] = h[cnt];  // 用堆中的最后一个元素替换堆顶元素cnt--;  // 堆中元素个数减 1down(1);  // 调整堆，保持最小堆的性质}return 0;
}