当前位置：首页 > news >正文

第五章决策树

news 2025/6/15 5:31:28

5.1 决策树模型与学习

说起决策树来，它不是一般的树，而是有理想有抱负的树，那么为什么这么讲呐？

5.1.1 思维模式

人类有两大逻辑思维：归纳法和演绎法。决策树是为了实现某一个目标而构建的树形结构。

我想看一下情人节这一天，大家是怎么过的，以这个例子为例，建立一棵决策树：

由于是情人节，我们首先需要考虑的是是否是单身。

如果不是单身，那么当天的活动安排就要将对方考虑在内，如果对方需要陪伴，那么就是各种花式虐狗行为了；如果不需要陪伴，就要看你当天是否有任务，如果有任务，我们就安排去学习，没有任务的话，就安排一些娱乐活动了（比如：男生喜欢打游戏，女生则刷刷剧）。

如果是单身，可能会考虑提升自我，想提升自我的小伙伴，可能会考虑内修还是外练，想要内在气质提升，就可能会去学习，想提升外在，就可能去运动；还有一些在情人节不想提升自己的小伙伴，可能会去娱乐。

以上就是一棵决策树，当然这是我们主观构造的决策树，现实生活中可能会更加复杂。kd树是二叉树，而决策树是多叉树。

现在我们看一个客观的例子，这是一个是否可以放贷款的例子：

5.1.2 模式结构

分类决策树模型是一种描述对实例进行分类的树形结构。

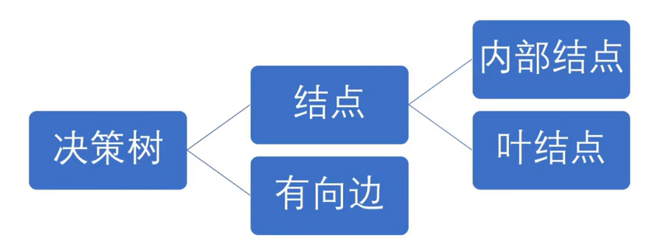
决策树由结点和有向边组成，结点又有内部结点和叶结点组成，其中，内部结点用圆圈表示，叶结点用方框表示。内部结点表示特征或属性，叶结点表示类别。

决策树是通过一系列规则（if-then）对数据进行分类的过程。其实从本质上来说，决策树就是从根节点到叶节点的过程。从根节点出发到叶节点所经过的称为路径，而这条路径就对应着一条规则，这条规则是用if-then组成的。

先判断是否是单身，如果不是的话，看对方是否需要陪伴；如果不需要陪伴，看你是否有任务；如果有任务的话就得到一个学习的活动安排。

我们现在看一下是不是每一个叶节点都对应着一个规则呢？是的，每一个叶节点都对应着一个规则，而且每一个叶节点所对应的规则都不一样。一个叶节点或一个类，它可能对应多条路径，但是每一个实例都对应着一条路径。

If-then规则是互斥且完备的。互斥是指这个属性所分的叉，它是互相之间没有交集；完备是指分完地叉合在一起是合集。

构建决策树的规则如下：

5.1.3 条件概率分布

对于决策树而言，表示给定特征条件下类的条件概率分布P(Y|X)，这就是说，决策树可以表示成在给定的特征条件下类的条件概率分布；而条件概率分布对应着特征空间的一个划分，如果我们有十个条件概率分布，对应着特征空间的十个划分，其实就相当于我们构建了十棵决策树，至于哪一棵决策树表现更好，就要看决策树学习了。

特征空间是由特征向量组成的，而特征向量用来表示输入的每一个实例，所以一般情况下我们可以认为输入空间与特征空间是相同的。比如说，下图中所表示的特征空间是： $\begin{Bmatrix} x=(x^{(1)},x^{(2)})^{T}|0\leq x^{(1)}\leq 1,0\leq x^{(2)}\leq 1 \end{Bmatrix}$ 。我们想要得到一个决策树，就需要将这个特征空间划分出来，划分完成后，就得到了一个完整的条件概率分布了。

在划分时，我们所得到的单元或区域是互不相交的，而且这些单元或者区域合在一起就是我们的整个特征空间。我们在讲决策树的规则时，是这样解释路径的互斥和完备的，而且恰好这里的每一个单元其实就是对应着我们之前讲的if-then规则的集合所组成的一条路径，一个单元对应着一条路径。

假如说，我们现在已经完成了对特征空间的划分，将其划分为一个又一个的小单元或小区域可是每个单元或者区域，它所对应的类别是怎么确定的呐？比如说，某个单元c的条件概率满足 $P(Y=+1|X=c)> 0.5$ 时，认为该单元属于正类;某个单元c的条件概率满足 $P(Y=-1|X=c)> 0.5$ 时，认为该单元属于负类。

我们现在由刚才看到的一个平面图变换成一个立体图形来看：

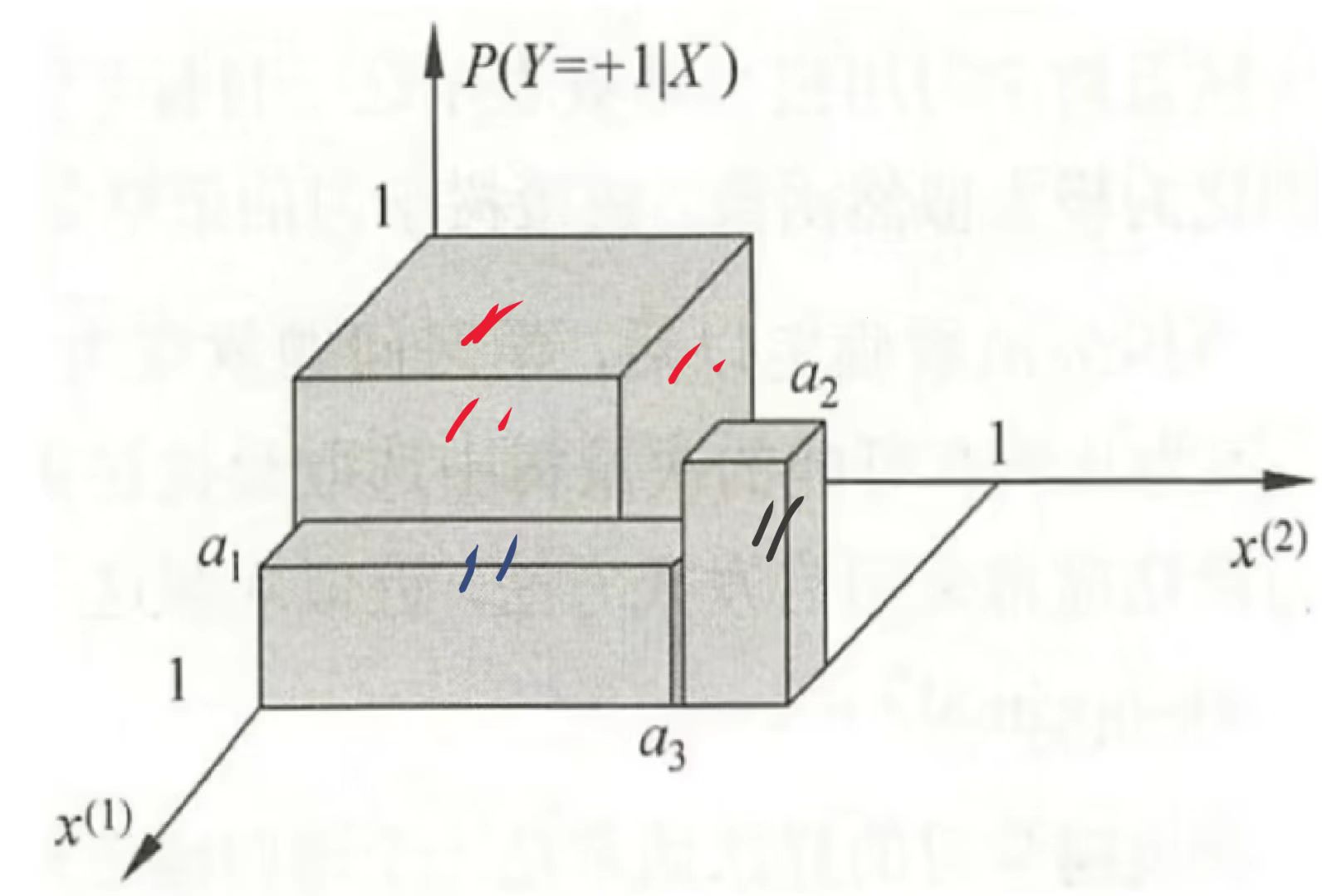
这个立体图形中包含了y=+1的条件概率，我们看一下对于用红色记号标记的区域而言，y=+1的条件概率是大于0.5，这个区域就是正类；对于用蓝色记号标记的区域而言，y=+1的条件概率是小于0.5，这个区域就是负类；对于黑色记号标记的区域而言，y=+1的条件概率是大于0.5，这个区域就是正类。

现在我们一直讲的是两个类别的分类，所以只需要与0.5比大小就可以了；如果我们分了多个类，我们只需呀看一下它们分别的条件概率，，哪一个类的条件概率大，那么就属于哪一个类。

假如，我们将特征空间划分成四个单元，这四个单元命名如下：

这四个单元在决策树中如下：

这就说明，对于决策树而言，特征空间中所划分的每一个单元都对应着决策树中的一条路径；决策树的条件概率分布由各个单元给定条件下类的条件概率分布组成。

5.1.4 决策树学习

已知：训练集 $T=\begin{Bmatrix} (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N}) \end{Bmatrix}$ ，其中 $x_{i}=(x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})^{T}$ ， $y_{i}\in \begin{Bmatrix} 1,2,...,k \end{Bmatrix}$ ，i=1,2,...,N

目的：构造决策树，并对实例正确分类

我们看一个贷款申请的例子：

在这个例子中，我们发现有三个特征（n=3，年收入、房产、婚姻状况），两种类别（k=2，可以偿还、无法偿还）。假如我们现在已经根据数据集T得到了这棵决策树，现在我们判一下实例：年收入 $x^{(1)}$ 为75万， $x^{(2)}$ 为无房产，婚姻状况 $x^{(3)}$ 为单身。对于这个实例而言，我们根据决策树可以得到的类别是无法偿还。

构造决策树过程中，产生的问题有：

1.我们根据同一个训练数据集可以构造出几种决策树？

2.在构造决策树过程中，以首选哪一个特征进行分类？第二个、第三个特征又是怎么确定的？

3.如果我们有一个复杂的决策树，我们应该怎么办？

决策树的本质就是从训练数据集T中归纳出一组分类规则，这组规则要与训练数据集不相矛盾。我们可能能训练出无穷多个条件概率模型，一棵好的决策树与训练数据矛盾较小（对已知数据的拟合能力强），同时具有很好的泛化能力（对未知数据的预测能力）。

我们怎样训练出一个模型呐？它的策略就是通过最小化损失函数来实现，而有可能是有无穷多个决策树，决策树树与决策树之间是有区别的，也就是每次选择的特征可能不一样。如何选择最优特征，就是特征选择（递归选择最优特征）将要面临的问题。当对应特征空间有了基本划分，直到所有的训练子集被基本正确划分类就停止我们的算法，之所以这里强调“基本正确分类”而不是“全部正确分类”其实就是为了避免过拟合，为了平衡拟合能力和泛化能力。如果决策树过于枝繁叶茂，为了避免过拟合，具有更好的泛化能力就需要剪枝。

剪枝可以分为预剪枝和后剪枝。预剪枝：比如我们要经营一片果园，我们的目的是想结果，所以果农通常需要修剪果树，使果树不要过高。这样既利于果子得到充足的营养，又避免果树过高而难以采摘，这是在树成长前剪枝。后剪枝：园艺工人为大树修剪特定的形状，这是在树成长后进行剪枝。

5.2 特征选择

我们为什么要对决策树进行特征选择？我们怎样选择出最优的特征？

5.2.1 特征选择问题

我们来看一个例子：这是一个由15个样本组成的贷款申请训练数据。数据包括贷款申请人的4个特征：第1个特征是年龄，有3个可能值：青年，中年，老年；第2个特征是有工作，有2个可能值：是，否；第3个特征是有自己的房子，有两个可能值：是，否；第4个特征是信贷情况，有两个可能值：非常好，好，一般。有两个类别，可能值为：是，否。

希望通过对所给的训练数据学习一个贷款申请的决策树，用以对未来的贷款申请进行分类，即当新的客户提出贷款申请时，根据申请人的特征利用决策树决定是否批准贷款申请。

如果我们第一个特征选择年龄的话，可以得到下面这样的决策树：

如果以有无工作这个特征作为第一个特征构建决策树，绘制出来的决策树如下：

根据上面这两个决策树我们发现，当我们逊选择不同的特征作为决策树的第一个特征进行构建，所构建出来的决策树是不一样的。当选择年龄作为决策树的一个个特征，我们发现决策树比较复杂；当选择有无工作作为决策树的第一个特征，我们发现构建的决策树比较简单。那么我们该如何选择最优特征呐？

5.2.2 信息增益

信息增益由熵构建而成，熵用来表示随机变量的不确定性。如果随机变量有n个取值的话，每个取值所对应的概率是 $p_{i}$ ，那么这个随机变量x的熵 $H(x)=-\sum_{i=1}^{n}p_{i}logp_{i}$ ，由于此处的熵是和随机变量x的分布有关系，所以也可以表示成 $H(p)=-\sum_{i=1}^{n}p_{i}logp_{i}$ ，这个p就对应着随机变量的分布。

当随机变量的取值等概率分布的时候，相应的熵最大。为什么随机变量的取值等概率分布的时候最大呐？我们通过一个简答的例子计算一下。

假如我们此处的随机变量只有两个取值，一个是1，一个是0，x取1的概率是p，取0的概率是q=1-p，这个随机变量x所对应的熵 $H(x)=-plog_{2}p-(1-p)\cdot log_{2}(1-p)$ ，绘制p和H(p)的图形如下：

当p=0.5时，熵取最大值H(p)=1，除了通过图像的方式知道最大值，还可以通过求导的方式得到最大值。当是凹函数时，可以用求导的方式取得最大值；当时凸函数时，可以用求导的方式得到最小值。

条件熵： $H(Y|X)=-\sum_{i=1}^{n}p_{i}H(Y|X=x_{i})$ 。当熵和条件熵中的概率是由数据估计得到时，则为经验熵和经验条件熵；当熵和条件熵中的概率对应着真是分布的时候，那就是理性熵和真是条件熵。信息增益就是熵减去条件熵，而熵和条件熵都是根据训练数据集计算出来的经验熵和经验条件熵，即 $g(D,A)=H(D)-H(D|A)$ 。

为什么用这样一个差值代表信息增益？上式所对应的D就是训练数据集，H(D)是我们在不知道任何信息的情况下得到的熵，假如我们知道x的某个特征信息A，在已知特征信息的情况下，训练数据集有了一个重新的分类，此时所对应的熵就是根据这个特征信息A而发生的变化。变化越大，就说明由于增加了A特征而更加确定。因此，哪一个特征所带来的信息增益越大，就应该选择哪一个特征作为最优特征。这就是信息增益的作用。

我们具体看一下怎样对信息增益进行求解：

我们现在知道训练数据集D和特征A，期望得到特征A关于D的信息增益g(D,A)。首先计算经验熵，再计算经验条件熵，信息增益就是经验熵减去经验条件熵。

现在通过例题看一下信息增益的计算，继续以贷款例子为例：

经验熵公式为： $H(D)=-\sum_{k=1}^{K}\frac{\left | C_{k} \right |}{\left | D \right |}log_{2}\frac{\left | C_{k} \right |}{\left | D \right |}$

我们把这个训练集记作D，其中包含15个样本，如果不加任何特征的话，我们最终想分为两个类别（不同意贷款，同意贷款），所以类别 K=2， $C_{k}$ 对应不附加任何特征的情况下，它所分的类别。假如 $C_{1}$ 对应不同意贷款，我们发现其中包含了6个样本； $C_{2}$ 对应着同意贷款，包含9个样本。这里的经验熵是根据训练数据集计算出来的，也就是说这个概率是根据D得到的。根据这个训练集得到的不同意贷款的概率是 $\frac{6}{15}$ ，同意贷款的概率是 $\frac{9}{15}$ ，所以此处的经验熵 $H(D)=-\frac{6}{15}log_{2}\frac{6}{15}-\frac{9}{15}log_{2}\frac{9}{15}=0.971$ ，这是不加任何特征的情况下所得到的训练数据集的熵。

接下来我们分别看一下，当我们加上特征的时候所得到的经验熵是多少，这时候计算的就是经验条件熵 $H(D|A)=\sum_{i=1}^{n}\frac{\left | D_{i} \right |}{\left | D \right |}H(D_{i})=-\sum_{i=1}^{n}\frac{\left | D_{i} \right |}{\left | D\right |}\sum_{k=1}^{K}\frac{\left | D_{ik} \right |}{\left | D \right |}log_{2}\frac{\left | D_{ik} \right |}{\left | D \right |}$ 。假如说我们现在加入年龄这一个特征，我们发现根据年龄这一个特征，可以将原本的训练数据集D划分为3个子集：有5个青年子集 $D_{1}$ ，其中有3个样本是不同意贷款，2个样本是同意贷款；5个中年子集 $D_{2}$ ，其中有2个样本是不同意贷款，3个样本是同意贷款；5个老年子集 $D_{3}$ ，其中有1个样本是不同意贷款，4个样本是同意贷款。具体如下表：

下面，我们就可以计算经验条件熵了。经验条件熵就是在给定特征A后所得到的n个子集，每个子集计算它的熵，然后进行加权求和。那么我们在给定年龄这个特征的时候，它划分出3个子集，所以n=3，每个权重就是 $D_{i}$ 中所包含的样本个数与训练数据集D中样本个数的比例。

$H(D|A_{1})=\frac{5}{15}H(D_{1})+\frac{5}{15}H(D_{2})+\frac{5}{15}H(D_{3})=\frac{5}{15}(-\frac{3}{5}log_{2}\frac{3}{5}-\frac{2}{5}log_{2}\frac{2}{5})+\frac{5}{15}(-\frac{2}{5}log_{2}\frac{2}{5}-\frac{3}{5}log_{2}\frac{3}{5})+\frac{5}{15}(-\frac{1}{5}log_{2}\frac{1}{5}-\frac{4}{5}log_{2}\frac{4}{5})=0.888$

下面我们看一下“有工作”这一个特征。我们可以将训练数据集分成2个子集：

$D_{1}$ 对应有工作，有5个样本个数； $D_{2}$ 对应无工作，有10个样本个数。

$H(D|A_{2})=\frac{5}{15}\cdot H(D_{1})+\frac{10}{15}\cdot H(D_{2})=\frac{5}{15}\cdot (-0log_{2}0-\frac{5}{5}log_{2}\frac{5}{5})+\frac{10}{15}\cdot (-\frac{6}{10}log_{2}\frac{6}{10}-\frac{4}{10}log_{2}\frac{4}{10})=0.647$

下面我们看一下“有工房子”这一个特征。我们可以将训练数据集分成2个子集：

$D_{1}$ 对应有自己的房子，有6个样本个数； $D_{2}$ 对应没有自己的房子，有9个样本个数。

$H(D|A_{3})=\frac{6}{15}\cdot H(D_{1})+\frac{9}{15}\cdot H(D_{2})=\frac{6}{15}\cdot (-0log_{2}0-\frac{6}{6}log_{2}\frac{6}{6})+\frac{9}{15}\cdot (-\frac{3}{9}log_{2}\frac{3}{9}-\frac{6}{9}log_{2}\frac{6}{9})=0.551$

下面我们看一下“信贷情况”这一个特征。我们可以将训练数据集分成3个子集：

$D_{1}$ 对应信贷情况非常好，有4个样本个数； $D_{2}$ 对应信贷情况好，有6个样本个数； $D_{3}$ 对应信贷情况一般，有5个样本个数。

$H(D|A_{3})=\frac{4}{15}H(D_{1})+\frac{6}{15}H(D_{2})+\frac{5}{15}H(D_{3})=\frac{4}{15}\cdot (-0log_{2}0-\frac{4}{4}log_{2}\frac{4}{4})+\frac{6}{15}\cdot (-\frac{2}{6}log_{2}\frac{2}{6}-\frac{4}{6}log_{2}\frac{4}{6})+\frac{5}{15}\cdot (-\frac{4}{5}log_{2}\frac{4}{5}-\frac{1}{5}log_{2}\frac{4}{5})=0.608$

因此，相应的信息熵、信息经验熵、信息增益如下：

5.2.3 信息增益比

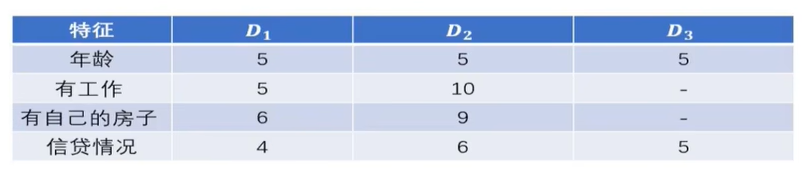
除了信息增益，还可以通过信息增益比来选择最优特征。为什么有了信息增益，还要定义一个信息增益比？这是因为信息增益有时候更倾向于选择具有更多取值的特征，比如说信贷情况有3个取值，有工作有两种取值，那么这时候信贷情况的取值个数是多于有工作的取值个数的。由于信贷情况的取值个数较多，有可能由于这个原因造成它的信息增益是大于有工作的。信息增益比就可以降低由于特征取值较多所造成影响。信息增益比就是在信息增益的基础上增加一个惩罚项。这个惩罚项就是训练数据集D关于特征A的熵的倒数，信息增益比是 $\frac{g(D,A)}{H_{A}(D)}$

$H_{A_{1}}(D)=-\frac{5}{15}log_{2}\frac{5}{15}-\frac{5}{15}log_{2}\frac{5}{15}-\frac{5}{15}log_{2}\frac{5}{15}=1.585$

$H_{A_{2}}(D)=-\frac{5}{15}log_{2}\frac{5}{15}-\frac{10}{15}log_{2}\frac{10}{15}=0.918$

$H_{A_{3}}(D)=-\frac{6}{15}log_{2}\frac{6}{15}-\frac{9}{15}log_{2}\frac{9}{15}=0.971$

$H_{A_{4}}(D)=-\frac{4}{15}log_{2}\frac{4}{15}-\frac{6}{15}log_{2}\frac{6}{15}-\frac{5}{15}log_{2}\frac{5}{15}=1.566$

算出的信息增益比如下：

对比“有工作”和“信贷情况” 这两个特征的信息增益，我们会选择信息增益较大的“信贷情况”作为最优特征，也就是选择信贷情况这个值可以带来更大的确定性；如果引入信息增益比来消除特征个数的不同所带来的影响，这时候选择“有工作”这个特征来作为最优特征。

对于信息增益和信息增益比，这两个孰优孰劣？信息增益的缺点是倾向于选择取值较多的特征；而信息增益比倾向于选择取值较少的特征。选择哪一个需要根据实际情况而定。

5.3 决策树的生成

5.3.1 ID3算法

ID3算法是使用信息增益进行特征选择。

ID3算法如下：

输入：训练数据集D、特征集A、阈值 $\epsilon$

输出：决策树T

（1）判断T是否需要选择特征生成决策树。

不需要进行特征选择：

①如果所有的实例点都属于同一个类，则T是单结点树，记录实例类别 $C_{k}$ ，以此作为该节点的类标记。例如现在有10天的天气数据，每一天的数据包含了湿度、温度、风力等特征，但是这10天都是晴天，也及时这些实例点都属于同一类。

②当特征集 $A=\varnothing$ 时，则T是单结点树，记录实例个数最多类别 $C_{k}$ ，以此作为该节点的类标记。假如现在有10天的天气数据，其中8天是晴天，2天不是晴天，除此之外，没有关于天气的任何特征数据。没有特征。自然就不需要特征选择了。

需要进行特征选择，就计算A中各特征的信息增益，并选择信息增益最大的特征 $A_{g}$ :

①若 $A_{g}$ 的信息增益小于 $\epsilon$ ，则说明 $A_{g}$ 这个特征并不会给分类带来更多的确定性，也就是说它并没有有助于分类。既然这个信息增益最大的特征对分类都没有很大的帮助，就更别说其他特征了。这时我们可以认为这棵决策树是一个单结点树，记录D中实例点个数最多类别 $C_{k}$ ，以此作为该结点的类标记。

②若 $A_{g}$ 的信息增益大于 $\epsilon$ ，我们可以将训练数据集D根据 $A_{g}$ 这个特征的所有可能取值 $a_{i}$ 划分为若干个非空子集 $D_{i}$ ，将 $D_{i}$ 中实例个数最多的类别作为标记，构建子节点

（2）第i个子节点，以 $D_{i}$ 为训练集， $A-A_{g}$ 为特征集合，递归地调用以上步骤，直到为单一结点后停止。

下面我们看一个例子：

这是一个贷款申请的数据集。这个数据集中包含了15个训练样本，其中有9个是同意贷款，6个是不同意贷款，这说明所有的实例点并不属于同一个类；这个训练样本集包含了4个特征，说明特征集A不是空集，因此，这并不是一个单节点的决策树，我们需要进行下一步的判断。

接下来，我们计算每一个特征所对应的信息增益：

我们发现这里的信息增益值是比较大的，也就是说，即使我们人为的给定一个阈值，比如 $\epsilon =0.001$ ，那么这里的四个信息增益值没有一个是小于阈值的，所以依然不可以认为这是一个单节点的决策树，我们需要选择信息增益最大的进行决策树的生成。

这里信息增益最大的特征是“有自己的房子”，我们现在就将根节点确定下来了。

当“有自己的房子”将整个训练集D划分为 $D_{1}$ 和 $D_{2}$ 时， $D_{1}$ 中的所有实例都是同意贷款的；而 $D_{2}$ 中有6个是同意贷款的，3个不同意贷款。

我们画一个这个决策树，如下：

根节点处就是有自己的房子，如果有自己的房子，那么所对应到的所有实例都是同意贷款，那么就得到一个叶子结点（同意贷款的类别）；但如果没有自己的房子，这时候所对应的 $D_{2}$ 既有同意贷款，又有不同意贷款，我们就需要根据特征选择来找到这个内部结点所对应的特征。

下面，我们就以 $D_{2}$ 作为新的训练数据集， $A_{1},A_{2},A_{4}$ 作为新的特征集来计算各个特征的信息增益。

计算 $g(D_{2},A_{1})$ 的信息增益。 $g(D_{2},A_{1})=H(D_{2})-H(D_{2}|A_{1})$ ，其中

经验熵 $H(D_{2})=-\frac{6}{9}log_{2}\frac{6}{9}-\frac{3}{9}log_{2}\frac{3}{9}=0.918$ ；

经验条件熵 $H(D_{2}|A_{1})=\frac{4}{9}(-\frac{1}{4}log_{2}\frac{1}{4}-\frac{3}{4}log_{2}\frac{3}{4})+\frac{3}{9}(-\frac{2}{3}log_{2}\frac{2}{3}-\frac{1}{3}log_{2}\frac{1}{3})=0.667$

信息增益为0.251

我们接下来算一下第二个特征，也就是对“有工作”这个特征而言：

经验条件熵 $H(D_{2}|A_{2})=\frac{3}{9}H(D_{21})+\frac{6}{9}H(D_{22})=0$

信息增益为0.918

接下来计算“信贷情况”这个特征的经验条件熵：

经验条件熵 $H(D_{2}|A_{4})=\frac{4}{9}(-\frac{2}{4}log_{2}\frac{2}{4}-\frac{2}{4}log_{2}\frac{2}{4})=0.444$

信息增益为0.474

现在我们整理一下：

我们发现“有工作”这个特征所对应的信息增益最大，所以我们接下来的内部节点就对应着“有工作”这个特征，相应的决策树如下：

我们发现，对于这个例题而言，整棵决策树只用了两个特征，这是因为我们在选择了第二个特征后所得到的两个小子集都是同属于同一类别的，所以就停止了。

5.3.2 C4.5算法

C4.5算法是使用信息增益比进行特征选择。C4.5算法是非常有名的算法。

C4.5算法就是将上述ID3算法的信息增益改成信息增益比。使用信息增益比来构建决策树，它可以克服之前信息增益选择特征时，可能会偏向取值较多的特征的问题；而且相较于ID3算法，C4.5算法不仅可以处理离散型的描述特征，还可以处理连续型的。所以说C4.5算法在继承ID3算法的一些优点外，还有自己的优点。不过C4.5算法也有一定的缺点：信息增益比的计算麻烦，尤其实是在处理连续型变量时。因此C4.5算法虽然解释起来比较容易，但是在决策树的生成过程中需要对数据进行多次的顺序扫描和排序，导致算法的低效性。也就是说，当我们的数据量非常大时，这个程序很难运行。

查看全文

http://www.xdnf.cn/news/1031923.html