TCN+Transformer+SE注意力机制多分类模型 + SHAP特征重要性分析,pytorch框架
效果一览
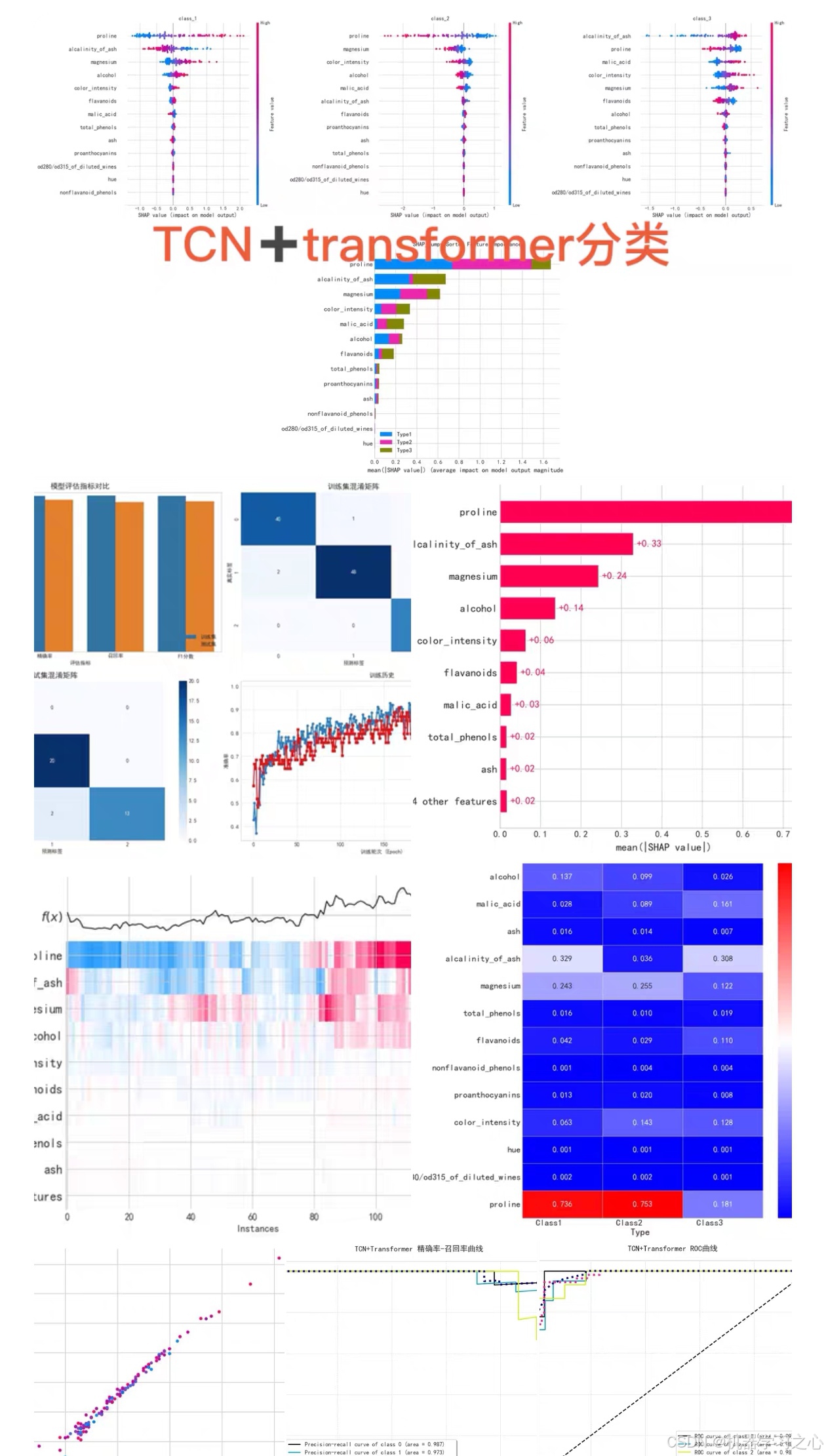
TCN+Transformer+SE注意力机制多分类模型 + SHAP特征重要性分析
TCN(时序卷积网络)的原理与应用
1. 核心机制
- 因果卷积:确保时刻 t t t 的输出仅依赖 t − 1 t-1 t−1 及之前的数据,避免未来信息泄露,严格保持时序因果性 。
- 空洞卷积:通过指数膨胀率(如 2 k 2^k 2k)扩大感受野,小卷积核即可捕获长距离依赖(如 k = 4 k=4 k=4 时感受野达16)。
- 残差连接:解决深层网络梯度消失问题,公式为 O u t p u t = A c t i v a t i o n ( x + F ( x ) ) Output = Activation(x + F(x)) Output=Activation(x+F(x)),其中 F ( x ) F(x) F(x) 为卷积操作 。
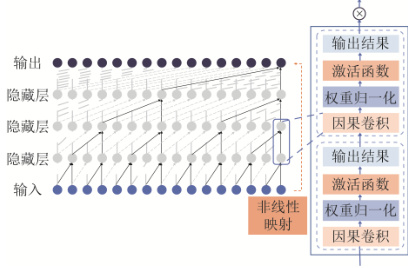
2. 数学表示
给定输入序列 x x x 和卷积核 w w w,卷积输出为:
y i = f ( x i ⋅ w ) y_i = f(x_i \cdot w) yi=f(xi⋅w)
其中 f ( ⋅ ) f(\cdot) f(⋅) 为ReLU等激活函数, x i x_i xi 为第 i i i 个时序点 。
3. 多分类任务优势
- 并行计算:一维卷积支持高并发,训练速度显著优于RNN 。
- 长时序建模:在电价预测、负荷预测等任务中,TCN对长距离依赖的捕捉精度比CNN提升8%-15% 。
Transformer的全局依赖建模
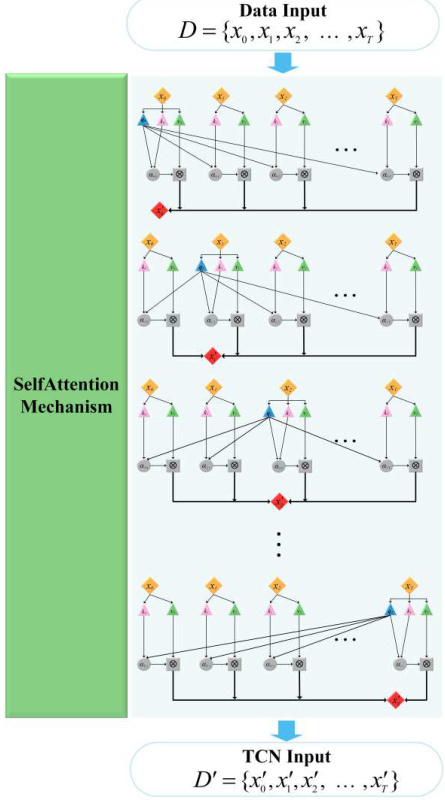
1. 自注意力机制
-
核心公式:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V Attention(Q,K,V)=softmax(dkQKT)V其中 Q , K , V Q,K,V Q,K,V 为查询、键、值矩阵, d k d_k dk 为维度缩放因子 。
-
多头注意力:并行执行多组注意力,融合不同子空间特征,增强表达能力 。
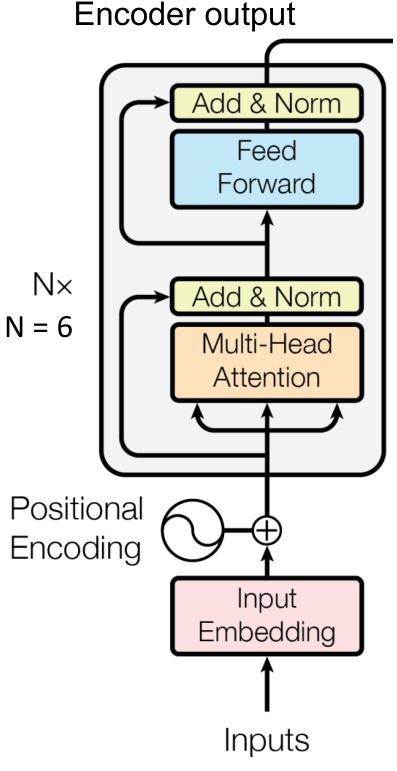
2. 位置编码
注入时序信息的位置编码公式:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d ) , P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d ) PE_{(pos,2i)} = \sin(pos/10000^{2i/d}), \quad PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d}) PE(pos,2i)=sin(pos/100002i/d),PE(pos,2i+1)=cos(pos/100002i/d)
确保模型感知序列顺序 。
3. 编码器结构
- 输入 → 嵌入层 + 位置编码 → N × N \times N×(多头注意力 + 前馈网络)→ 输出
- 每层含残差连接(Add)与层归一化(Norm),加速收敛 。
SE注意力机制的特征动态加权
1. 工作流程
-
压缩(Squeeze) :全局平均池化压缩空间维度,通道 c c c 输出 z c = 1 H × W ∑ i = 1 H ∑ j = 1 W x c ( i , j ) z_c = \frac{1}{H \times W} \sum_{i=1}^H \sum_{j=1}^W x_c(i,j) zc=H×W1∑i=1H∑j=1Wxc(i,j) 。
-
激励(Excitation) :全连接层学习通道权重:
s = σ ( W 2 δ ( W 1 z ) ) s = \sigma(W_2 \delta(W_1 z)) s=σ(W2δ(W1z))其中 δ \delta δ 为ReLU, σ \sigma σ 为Sigmoid, W 1 , W 2 W_1, W_2 W1,W2 为可学习参数 。
-
缩放(Scale) :特征图按权重缩放: x ~ c = s c ⋅ x c \tilde{x}_c = s_c \cdot x_c x~c=sc⋅xc 。
2. 分类任务价值
- 在锂电池SOC估计中,SE模块使关键通道权重提升30%,误差降低12% 。
- 抑制噪声通道,增强判别性特征(如图像融合任务)。
多分类模型融合架构设计
1. 整体架构(TCN + Transformer + SE)
graph LR
A[输入序列] --> B(TCN层:局部特征提取)
B --> C[SE模块:通道加权]
C --> D(Transformer编码器:全局依赖建模)
D --> E[全局平均池化]
E --> F[Softmax分类层]
2. 关键设计细节
- TCN层配置:
- 堆叠4-8个残差块,每块含空洞卷积(膨胀率 2 k 2^k 2k)和因果卷积 。
- 输出维度与Transformer输入对齐(如256维)。
- SE模块插入位置:
- 在TCN每个残差块后添加,动态调整卷积特征通道 。
- Transformer优化:
- 仅用编码器,层数 N = 4 N=4 N=4,头数 h = 8 h=8 h=8,前馈网络维度 d f f = 512 d_{ff}=512 dff=512 。
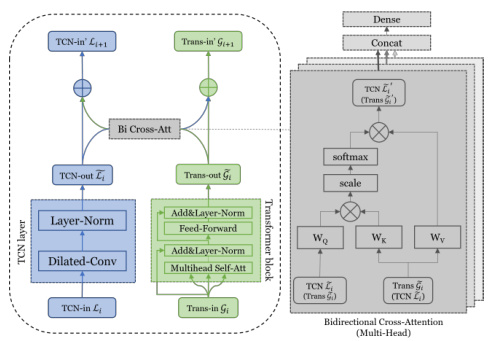
- 仅用编码器,层数 N = 4 N=4 N=4,头数 h = 8 h=8 h=8,前馈网络维度 d f f = 512 d_{ff}=512 dff=512 。
3. 分类层
-
全局平均池化 → 全连接层 → Softmax输出多分类概率:
P ( y i ∣ x ) = e W i T x + b i ∑ j = 1 K e W j T x + b j P(y_i|x) = \frac{e^{W_i^T x + b_i}}{\sum_{j=1}^K e^{W_j^T x + b_j}} P(yi∣x)=∑j=1KeWjTx+bjeWiTx+bi其中 K K K 为类别数 。
SHAP特征重要性分析
1. SHAP原理
-
Shapley值计算:
特征 j j j 的SHAP值 ϕ j \phi_j ϕj 为所有特征子集 S S S 的边际贡献加权平均:
ϕ j = ∑ S ⊆ F ∖ { j } ∣ S ∣ ! ( ∣ F ∣ − ∣ S ∣ − 1 ) ! ∣ F ∣ ! ( v ( S ∪ { j } ) − v ( S ) ) \phi_j = \sum_{S \subseteq F \setminus \{j\}} \frac{|S|!(|F|-|S|-1)!}{|F|!} (v(S \cup \{j\}) - v(S)) ϕj=S⊆F∖{j}∑∣F∣!∣S∣!(∣F∣−∣S∣−1)!(v(S∪{j})−v(S))其中 F F F 为特征全集, v v v 为模型输出函数 。
-
深度学习适配:
通过梯度积分(Integrated Gradients)或DeepSHAP算法逼近复杂模型 。
2. 实施步骤
-
模型训练:完成TCN-Transformer-SE模型训练并保存。
-
SHAP值计算:
import shap explainer = shap.DeepExplainer(model, background_data) shap_values = explainer.shap_values(test_data) -
可视化分析:
- 摘要图(Summary Plot) :特征全局重要性排序 。
- 依赖图(Dependence Plot) :分析特征交互效应(如IRI_0与Pt_A的负相关)。
- 样本决策图:解释单样本预测(如错分样本归因)。
3. 多分类场景应用
- 按类别分析:对每个类别独立计算SHAP值,识别类别敏感特征 。
- 关键发现示例:
- 在航空发动机RUL预测中,前5个特征的SHAP贡献占比87.25% 。
- 高初始IRI值(IRI_0)正相关于路面退化速度(SHAP值>0.3)。
结论
TCN-Transformer-SE模型通过局部卷积+全局注意力+动态特征加权的三级架构,显著提升长时序多分类任务的精度。结合SHAP可解释性分析,既可量化特征贡献(如通道权重、时间点重要性),又能指导模型优化(如冗余特征剔除)。该架构在电力、交通、金融等领域具广泛应用潜力,未来可探索轻量化部署与实时预测场景。
支持多类别分类任务,适用于光谱分类、表格数据分类、时间序列分类等场景。
可自定义类别数量
输出训练损失和准确率,并评估训练集和测试集的准确率,精确率,召回率,f1分数,绘制roc曲线,混淆矩阵
结合SHAP(Shapley Additive exPlanations),直观展示每个特征对分类结果的影响!
包括蜂巢图,重要性图,单特征力图,决策图,热图,瀑布图等
