当前位置：首页 > java >正文

机器学习通关秘籍｜Day 05：过拟合和欠拟合、正则化、岭回归、拉索回归、逻辑回归、Kmeans聚类

java 2025/9/2 11:12:24

一、欠拟合过拟合

1、欠拟合

2、过拟合

3、正则化

二、岭回归Ridge

1、损失函数

2、API

三、拉索回归Lasso

1、损失函数

2、API

四、逻辑回归

1、概念

2、原理

3、API

五、K-means算法

1、无监督学习

2、K-means算法

（1）什么是K-means？

（2）算法目标

（3）算法步骤（迭代过程）

（4）示例说明

（5）K-means 的优缺点

3、API

六、总结

一、欠拟合过拟合

在机器学习中，模型的性能通常受到两个关键问题的影响：欠拟合和过拟合。为了缓解这些问题，引入了正则化技术。

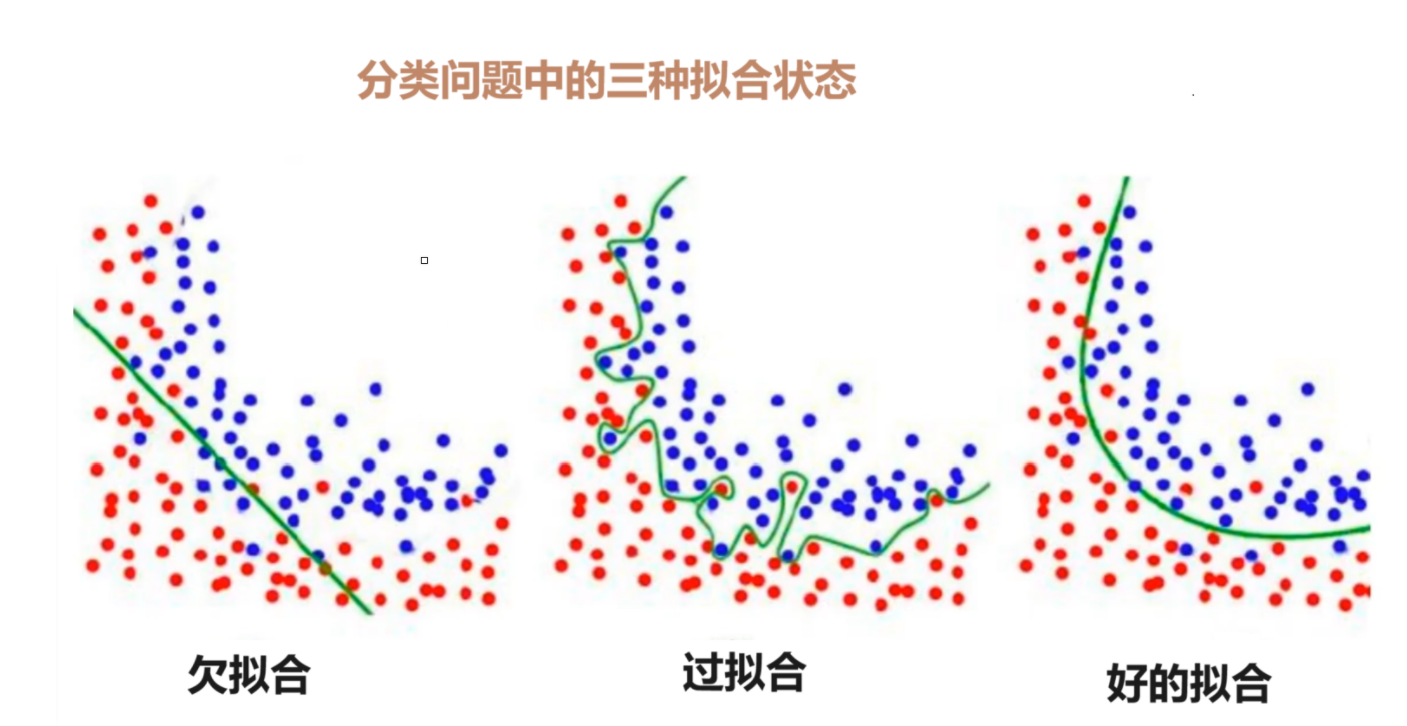
我们把拟合比作一个人的学习程度。欠拟合就是只学了一点，过拟合就是学过头了。欠拟合没有学习到正确的规律，而过拟合却是连“噪声点”的规律也学进去了。

通过上图，应该能让大家初步地理解欠拟合和过拟合。

1、欠拟合

定义：模型过于简单，无法捕捉到数据中的复杂模式。
表现：
- 训练集和测试集的误差都较高。
- 模型对数据的拟合程度不足，表现为低方差和高偏差。
原因：
- 模型复杂度太低（例如线性回归用于非线性数据）。
- 特征选择不当，忽略了重要特征。
解决方法：
- 增加模型复杂度（例如使用更高阶的多项式特征）。
- 增加特征数量或引入更多特征工程。
- 减少正则化强度（如果已经使用了正则化）。

2、过拟合

定义：模型 过于复杂，过度拟合训练数据，导致在新数据上的泛化能力较差。
表现：
- 训练集误差很低，但测试集误差很高。
- 模型对噪声非常敏感，表现为高方差和低偏差。
原因：
- 模型复杂度过高（例如高阶多项式回归）。
- 数据量不足，导致模型记忆噪声。
- 特征维度过高，导致模型参数过多。
解决方法：
- 简化模型（例如降低多项式的阶数）。
- 增加训练数据量。
- 使用正则化技术（如岭回归、拉索回归）。
- 使用交叉验证评估模型。

3、正则化

定义：通过增加额外的惩罚项 来限制模型的复杂度，从而防止过拟合。
原理：
- 在损失函数中加入正则化项，使得模型参数的值被约束在一个较小的范围内。
- 正则化项通常是模型参数的某种范数（如 L1 范数或 L2 范数）。
- 正则化可以平衡模型的拟合能力和泛化能力。
作用：
- 防止模型参数过大，避免过拟合。
- 提高模型的泛化能力，使其在新数据上表现更好。

正则化是一种防止过拟合的技术，通过在损失函数中加入惩罚项来限制模型的复杂度。

常见正则化方式：

L1 正则化（Lasso）：
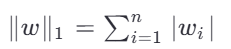
促使部分权重变为零，实现特征选择。
L2 正则化（Ridge）：
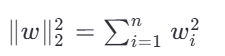
使权重变小但不为零，平滑模型输出。

在正则化公式中出现的符号 ‖·‖ 是 " 范数（Norm）" 的数学符号。它用来衡量向量（或矩阵）的“大小”或“长度”。在机器学习中，范数常用于衡量模型参数的复杂度，从而作为正则化项加入损失函数中，以防止过拟合。

✅ 正则化的本质是在偏差（Bias）和方差（Variance）之间取得平衡。

二、岭回归Ridge

岭回归是在普通最小二乘法基础上引入 L2 正则化的一种线性回归方法。

1、损失函数

标准线性回归的目标是最小化均方误差：

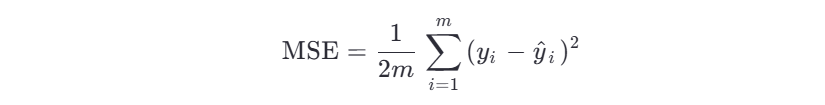
其中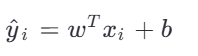

岭回归在损失函数中添加 L2 正则项：

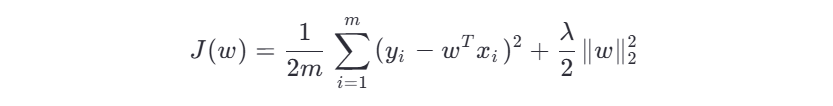
其中：

λ 是正则化系数（控制正则化强度）

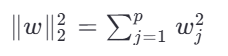
优化目标：找到使 J(w) 最小的权重向量 w 。

2、API

from sklearn.linear_model import Ridge
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split# 生成模拟数据
X, y = make_regression(n_samples=100, n_features=5, noise=10, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建岭回归模型
ridge = Ridge(alpha=1.0)  # alpha 对应 λ# 拟合模型
ridge.fit(X_train, y_train)# 预测
y_pred = ridge.predict(X_test)# 查看系数
print("系数:", ridge.coef_)
print("截距:", ridge.intercept_)

📌 注意：alpha 参数越大，正则化越强，模型越简单；太大会导致欠拟合。

三、拉索回归Lasso

拉索回归使用 L1 正则化，具有稀疏性特点，常用于特征选择。

1、损失函数

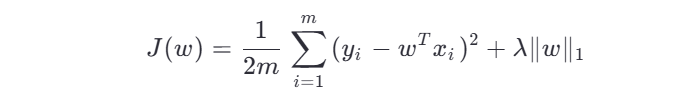
其中

由于 L1 的非光滑性，无法直接求导得到闭式解，通常采用坐标下降法或梯度下降法求解。

优点：

自动进行特征选择（部分权重被压缩为 0）
更适合高维稀疏数据

缺点：

当特征高度相关时，可能随机选择其中一个
解不唯一

2、API

from sklearn.linear_model import Lasso# 创建拉索回归模型
lasso = Lasso(alpha=1.0, max_iter=1000)# 拟合模型
lasso.fit(X_train, y_train)# 预测
y_pred = lasso.predict(X_test)# 查看系数（注意某些可能为0）
print("系数:", lasso.coef_)
print("截距:", lasso.intercept_)

🔍 可以观察到 lasso.coef_ 中某些值为 0，表示对应特征被剔除。

四、逻辑回归

逻辑回归虽然名字中有 “回归” ，但实际上是分类算法，主要用于 二分类问题。

1、概念

逻辑回归通过 Sigmoid 函数将线性组合映射到 [0,1] 区间，表示属于某一类的概率。

对于输入 x ，预测概率为：

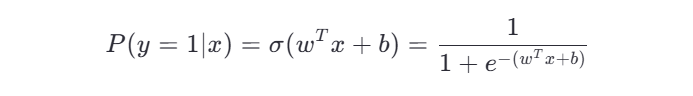
其中 σ(z) 是 sigmoid 函数。

2、原理

损失函数（交叉熵损失）

假设样本标签为 yi∈{0,1} ，则对数似然函数为：

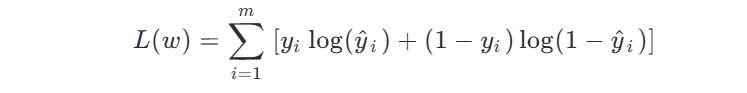
对应的损失函数为负对数似然：

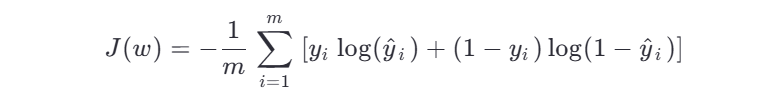
梯度更新公式：

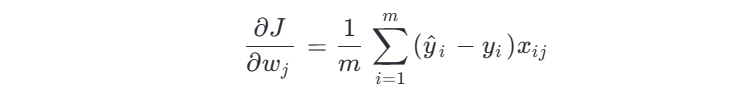
3、API

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification# 生成二分类数据
X, y = make_classification(n_samples=100, n_features=4, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建逻辑回归模型
log_reg = LogisticRegression()# 拟合
log_reg.fit(X_train, y_train)# 预测
y_pred = log_reg.predict(X_test)
y_proba = log_reg.predict_proba(X_test)  # 获取概率print("预测结果:", y_pred)
print("概率估计:", y_proba)

五、K-means算法

1、无监督学习

什么是无监督学习？

无监督学习（Unsupervised Learning） 是机器学习中的一种学习方式，它不依赖于带有标签的数据。换句话说，输入数据没有“正确答案”或“目标值”，模型的目标是从数据中发现隐藏的结构、模式或关系。

常见的无监督学习任务包括：

聚类（Clustering）
降维（Dimensionality Reduction）
异常检测（Anomaly Detection）

✅ K-means 就是一种典型的聚类算法，属于无监督学习范畴。

为什么需要无监督学习？

在现实世界中，很多数据是没有标签的。例如：

用户购物行为记录
社交网络中的用户互动
图像像素数据

这些数据虽然丰富，但没有明确的分类标签。通过无监督学习，我们可以将相似的数据点分组，从而揭示数据的内在结构。

2、K-means算法

（1）什么是K-means？

K-means（K-均值）是一种简单而有效的聚类算法，用于将数据集划分为 K个簇（clusters），使得每个数据点都属于离它最近的簇中心（质心）所代表的簇。

它的核心思想是：最小化簇内平方误差和（Within-cluster sum of squares, WCSS）。

（2）算法目标

给定一个数据集 X={x1,x2,...,xn} ，其中每个 xi 是一个 d 维向量，K-means 的目标是找到 K 个簇 C1,C2,...,CK ，并为每个簇分配一个中心点（质心）μj ，使得：

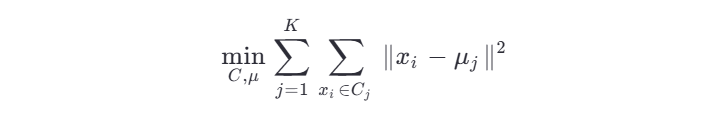
即：所有点到其所属簇中心的距离平方和最小。

（3）算法步骤（迭代过程）

K-means 算法是一个迭代优化算法，具体步骤如下：

1.初始化

随机选择 K 个数据点作为初始的簇中心（质心）。

2.分配阶段（Assignment Step）

对每个数据点 xi ，计算它到各个质心的距离，将其分配给距离最近的簇：

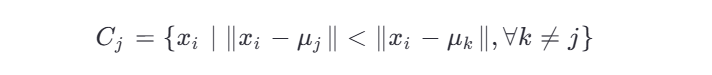
3.更新阶段（Update Step）

重新计算每个簇的质心（即该簇中所有点的均值）：

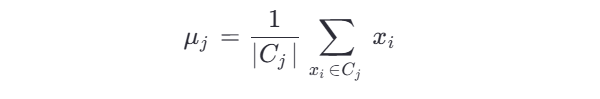
4.重复步骤 2 和 3

直到满足停止条件，如：

质心不再变化（收敛）
达到最大迭代次数
簇的分配不再改变

⚠️ 注意：K-means 可能会陷入局部最优解，因此通常运行多次取最佳结果。

（4）示例说明

假设我们有以下二维数据点：

(1, 1), (2, 1), (3, 1),

(1, 2), (2, 2), (3, 2),

(1, 3), (2, 3), (3, 3)

设定 K = 2。

随机选两个点作为初始质心，比如 (1,1) 和 (3,3)
计算每个点到这两个质心的距离，分配到最近的簇
更新质心（取每簇平均）
重复直到收敛

最终可能得到两个簇：左下区域和右上区域。

（5）K-means 的优缺点

优点	缺点
实现简单，易于理解	必须预先指定 K 值
计算效率高，适合大规模数据	对异常值敏感
结果可解释性强	只适用于球形簇（圆形/椭圆）
支持在线学习（部分变体）	初始质心影响结果（可能陷入局部最优）

3、API

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 随机种子
np.random.seed(42)
# 随机生成数据 int：整型
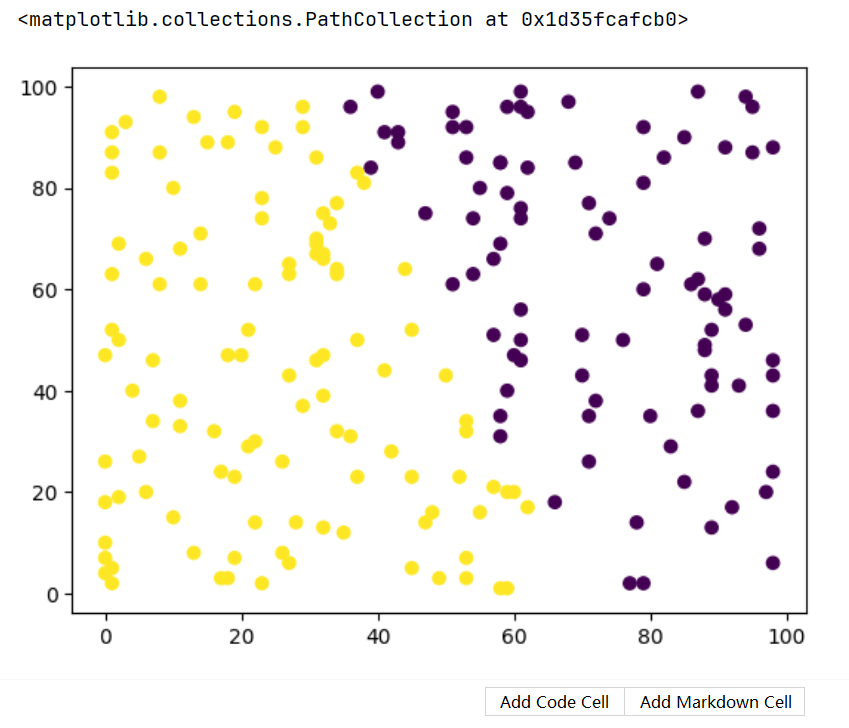
data = np.random.randint(0, 100, (200, 2))# 创建模型
model = KMeans(n_clusters=2)
# 训练模型
model.fit(data)
print(model.labels_)
print(model.cluster_centers_)x = data[:, 0]
y = data[:, 1]
# 绘制散点图
plt.scatter(x, y, c=model.labels_)