Python实现BP神经网络
1. BP神经网络
BP神经网络的核心思想是:通过前向传播计算输出,然后根据输出与真实值之间的误差,反向调整网络中的权重和偏置参数,使得网络的预测输出不断逼近真实值。
这个过程可以概括为:"前向传播计算输出,反向传播更新权重"。
第一阶段:准备与初始化
步骤1:搭建网络结构
确定网络有几层(输入层、隐藏层、输出层)
确定每层有多少个“神经元”(节点)
选择激活函数(如Sigmoid,决定神经元如何响应)
步骤2:准备数据
收集输入数据和对应的正确答案(标签)
将数据分为训练集和测试集
步骤3:初始化参数
给所有连接权重赋予很小的随机值(像随机设置一堆旋钮)
将偏置值设置为零
第二阶段:训练循环(重复以下步骤直到满足停止条件)
步骤4:前向传播(计算预测结果)
从输入层开始,将训练数据输入网络
数据经过隐藏层,每个神经元对收到的信号进行“加权求和”并加工处理
信号继续传递,最终到达输出层,产生预测结果
步骤5:计算误差(看看错多远)
将网络的预测结果与正确答案进行比较
计算两者之间的差距(误差)
这个误差值反映了当前网络预测的准确程度
步骤6:反向传播(找出谁的责任)
这是BP算法的核心:将输出层的误差反向传递回网络
逐层分析每个神经元对总误差的“贡献”大小
确定每个权重参数对误差应负的“责任”
步骤7:更新参数(调整旋钮)
根据每个参数的“责任”大小,按比例调整权重和偏置
调整方向是减少误差(让下次预测更准确)
学习率控制每次调整的幅度(小步调整更稳定,大步调整更快但可能不稳定)
步骤8:检查停止条件
如果达到最大训练次数,则停止
如果误差已经足够小,则停止
如果误差不再明显减小,则停止
第三阶段:测试与使用
步骤9:测试网络性能
使用未参与训练测试数据检验网络
评估网络在新数据上的预测能力
计算准确率等性能指标
步骤10:投入使用
将训练好的网络用于实际预测任务
输入新数据,网络给出预测结果
2.Python代码
import numpy as np
import matplotlib.pyplot as pltclass BPNeuralNetwork:def __init__(self, input_size, hidden_size, output_size):"""初始化BP神经网络:param input_size: 输入层神经元个数:param hidden_size: 隐藏层神经元个数:param output_size: 输出层神经元个数"""# 网络参数self.input_size = input_sizeself.hidden_size = hidden_sizeself.output_size = output_size# 初始化权重和偏置 (使用Xavier初始化)self.W1 = np.random.randn(self.input_size, self.hidden_size) * np.sqrt(1.0 / self.input_size)self.b1 = np.zeros((1, self.hidden_size))self.W2 = np.random.randn(self.hidden_size, self.output_size) * np.sqrt(1.0 / self.hidden_size)self.b2 = np.zeros((1, self.output_size))# 存储中间值用于反向传播self.z1 = Noneself.a1 = Noneself.z2 = Noneself.a2 = Nonedef sigmoid(self, x):"""Sigmoid激活函数"""return 1 / (1 + np.exp(-np.clip(x, -250, 250))) # 防止溢出def sigmoid_derivative(self, x):"""Sigmoid激活函数的导数"""return x * (1 - x)def forward(self, X):"""前向传播:param X: 输入数据:return: 网络输出"""# 第一层 (输入层 -> 隐藏层)self.z1 = np.dot(X, self.W1) + self.b1self.a1 = self.sigmoid(self.z1)# 第二层 (隐藏层 -> 输出层)self.z2 = np.dot(self.a1, self.W2) + self.b2self.a2 = self.sigmoid(self.z2)return self.a2def backward(self, X, y, output, learning_rate):"""反向传播更新权重:param X: 输入数据:param y: 真实标签:param output: 网络输出:param learning_rate: 学习率"""# 计算输出层的误差和梯度error_output = y - outputdelta_output = error_output * self.sigmoid_derivative(output)# 计算隐藏层的误差和梯度error_hidden = delta_output.dot(self.W2.T)delta_hidden = error_hidden * self.sigmoid_derivative(self.a1)# 更新权重和偏置self.W2 += self.a1.T.dot(delta_output) * learning_rateself.b2 += np.sum(delta_output, axis=0, keepdims=True) * learning_rateself.W1 += X.T.dot(delta_hidden) * learning_rateself.b1 += np.sum(delta_hidden, axis=0, keepdims=True) * learning_ratedef train(self, X, y, epochs, learning_rate, verbose=True):"""训练神经网络:param X: 训练数据:param y: 训练标签:param epochs: 训练轮数:param learning_rate: 学习率:param verbose: 是否打印训练过程:return: 训练损失历史"""losses = []for epoch in range(epochs):# 前向传播output = self.forward(X)# 计算损失 (均方误差)loss = np.mean(np.square(y - output))losses.append(loss)# 反向传播self.backward(X, y, output, learning_rate)# 打印训练进度if verbose and epoch % 1000 == 0:print(f"Epoch {epoch}, Loss: {loss:.6f}")return lossesdef predict(self, X):"""使用训练好的模型进行预测:param X: 输入数据:return: 预测结果"""return self.forward(X)def evaluate(self, X, y):"""评估模型性能:param X: 测试数据:param y: 真实标签:return: 准确率"""predictions = self.predict(X)# 对于二分类问题,将输出转换为0或1predicted_class = (predictions > 0.5).astype(int)accuracy = np.mean(predicted_class == y)return accuracy# 生成随机数据
def generate_data(num_samples=1000, input_size=3, noise_level=0.1):"""生成随机数据用于训练和测试这里创建一个简单的二分类问题:如果输入特征之和大于阈值则为1,否则为0"""# 生成随机输入特征X = np.random.randn(num_samples, input_size)# 创建标签:如果特征之和 > 0 则为1,否则为0y = (np.sum(X, axis=1) > 0).astype(int).reshape(-1, 1)# 添加一些噪声noise = np.random.randn(num_samples, 1) * noise_levely = np.clip(y + noise, 0, 1) # 确保标签在[0,1]范围内return X, y# 主程序
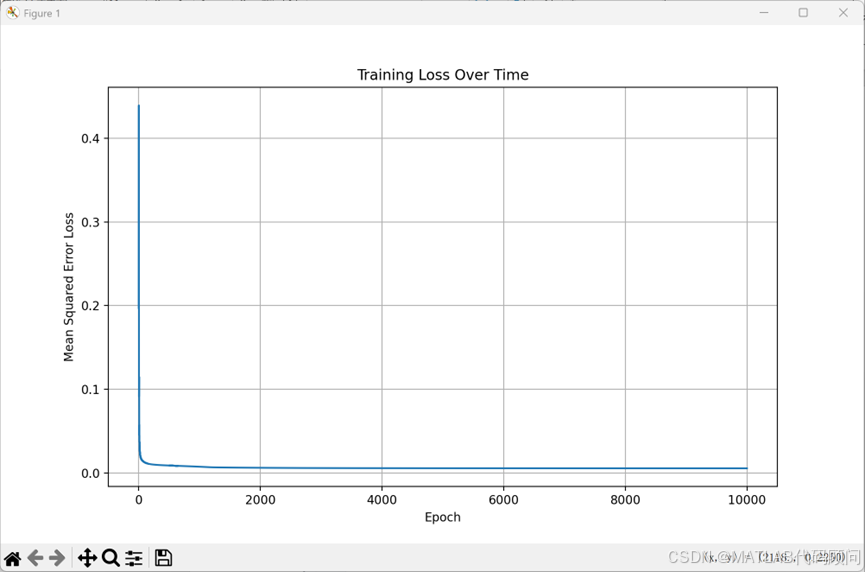
if __name__ == "__main__":# 设置随机种子以确保结果可重现np.random.seed(42)# 生成数据X, y = generate_data(num_samples=1000, input_size=3)# 划分训练集和测试集 (80% 训练, 20% 测试)split_idx = int(0.8 * len(X))X_train, X_test = X[:split_idx], X[split_idx:]y_train, y_test = y[:split_idx], y[split_idx:]print(f"训练集大小: {X_train.shape}")print(f"测试集大小: {X_test.shape}")# 创建神经网络实例input_size = X_train.shape[1] # 输入特征维度hidden_size = 4 # 隐藏层神经元数量output_size = 1 # 输出层神经元数量 (二分类问题)nn = BPNeuralNetwork(input_size, hidden_size, output_size)# 训练神经网络epochs = 10000learning_rate = 0.1print("开始训练...")losses = nn.train(X_train, y_train, epochs, learning_rate, verbose=True)# 评估模型train_accuracy = nn.evaluate(X_train, y_train)test_accuracy = nn.evaluate(X_test, y_test)print(f"\n训练准确率: {train_accuracy * 100:.2f}%")print(f"测试准确率: {test_accuracy * 100:.2f}%")# 绘制损失曲线plt.figure(figsize=(10, 6))plt.plot(losses)plt.title('Training Loss Over Time')plt.xlabel('Epoch')plt.ylabel('Mean Squared Error Loss')plt.grid(True)plt.show()# 进行一些预测示例print("\n预测示例:")for i in range(5):sample = X_test[i].reshape(1, -1)prediction = nn.predict(sample)actual = y_test[i]print(f"样本 {i + 1}: 预测值 = {prediction[0][0]:.4f}, 真实值 = {actual[0]}")3.程序结果
训练集大小: (800, 3)
测试集大小: (200, 3)
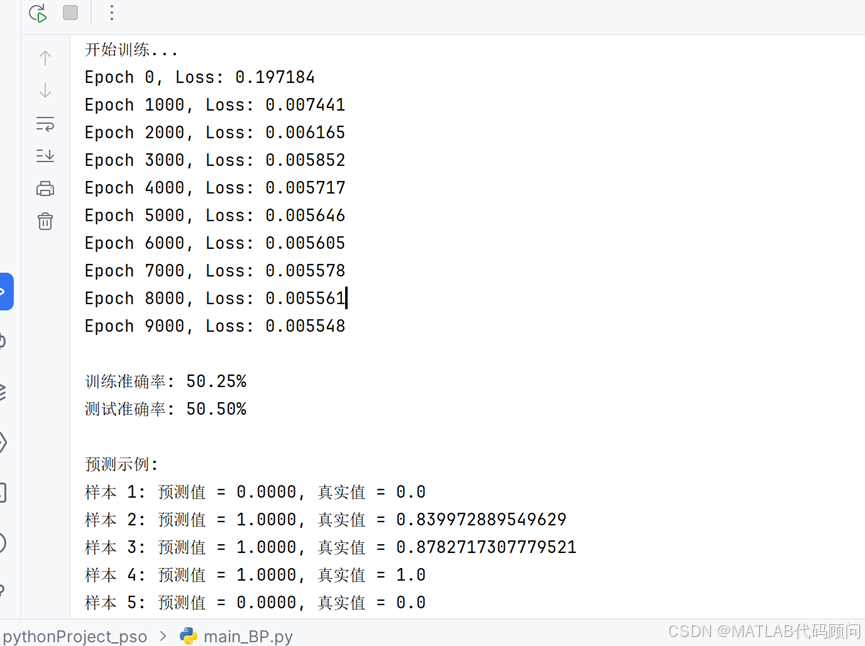
开始训练...
Epoch 0, Loss: 0.197184
Epoch 1000, Loss: 0.007441
Epoch 2000, Loss: 0.006165
Epoch 3000, Loss: 0.005852
Epoch 4000, Loss: 0.005717
Epoch 5000, Loss: 0.005646
Epoch 6000, Loss: 0.005605
Epoch 7000, Loss: 0.005578
Epoch 8000, Loss: 0.005561
Epoch 9000, Loss: 0.005548
训练准确率: 50.25%
测试准确率: 50.50%
预测示例:
样本 1: 预测值 = 0.0000, 真实值 = 0.0
样本 2: 预测值 = 1.0000, 真实值 = 0.839972889549629
样本 3: 预测值 = 1.0000, 真实值 = 0.8782717307779521
样本 4: 预测值 = 1.0000, 真实值 = 1.0
样本 5: 预测值 = 0.0000, 真实值 = 0.0
