数值分析——非线性方程与方程组的数值解法之二分法
非线性方程与方程组的数值解法——二分法
主要讨论非线性方程,也就是f(x)=0的情形,并且解都是实数,虚根和复根不属于讨论的范围。
f(x) = 0 ,其中x∈R,f(x)是连续函数,如果存在一个 x* 可以使得 f(x*) = 0 ,则我们就说x*是方程f(x)=0的根,从函数角度来说就是函数f(x)的零点。
进一步的,如果有: f(x) = (x - x*)m g(x) ,m∈N+(也就是m∈正整数),并且 g(x) ≠ 0 ,当 m = 1时,x* 就是这个方程的单根,或者也叫做函数 f(x) 的单零点,当 m ≥ 2 时,x* 就是方程的m重根,或者叫做函数 f(x) 的m重零点。
一般来讲,方程的最高次方其实就代表着有多少个解。
求根的步骤是先用图解法、解析法、定步长搜索法、近似方程法等方法搜索到根,再进一步将得到的根进行精确化。
或者也可以说第一步是对根进行隔离,得到隔离区间,第二步就是将近似值进行精确化。
二分法
逐步将含根的区间进行二等分,通过区间端点的函数值符号来进一步搜索含根区间,就这样反复进行区间分半后,最终使含根区间长度缩小到充分小,在这样一个足够小的区间内,方程有且仅有一个根,从而就可以求得满足给定精度要求的根的近似值。
图例说明:
f(x)=0,f(x) 是连续函数,假设 f(a) > 0,f(b) < 0, 那么 f(a) f(b) <0,此时选取a 与 b 的中点,假设a,b的中点为 a1,也就是a1 = (a+b)/2,先验证a1是否是零点,计算方程在a1处的值是否为0,

如果是零点就直接找到了方程的根,不是方程的零点时,就要看f(a1) 的正负号了,假设f(a1) >0,那么有 f(a1) f(b) <0,此时根的区间就重新选取为 [ a1,b],为了方便后面步骤的观察,重新令 b=b1,那么:

此时就有 f(a1) f(b1) <0,根在区间[ a1,b1]中,再取a1,b1的中点,假设为a2,也就是a2=(a1+b1)/2,再次判断a2这个点处是否是零点,(一般情况下没有那么简单,试一两次就直接试出来根的),不是根就再次判断a2处的函数值正负号,假设f(a2)>0,那么就有f(a2)f(b1)<0,根就在[a2,b1] 的区间中,令b1 = b2,那么:

得到一个新的根的隔离区间就是[a2,b2],以此类推,越分最后得到的区间就会越来越小,假设分了第 k 次后得到的根的隔离区间为[ak,bk]:

此时,确定x*在这个区间内,在二分的过程中,每一次区间长的变化就是:
b - a,(b-a)/ 2,(b-a)/ 22,(b-a)/ 23···(b-a)/ 2k,精确值x的近似取值就是:x = (aK + bk ) / 2,由于x,x*都是在[ak,bk] 区间内,
因此就有:
|x*- x| ≤ (bk - ak)/ 2
又因为一共分了k 次,所以[ak,bk]这个区间的长度就是(b - a)/ 2k,那么x与x 的区间长度关系就是:
|x- x| ≤(b - a)/ 2k+1,
又因为精确度是已知的(题目中都会具体给出要求):|x*- x| ≤ γ,这时就可以得到一个关系式:
(b - a)/ 2k+1 ≤ γ,里面一共就只有一个未知数k,计算出来即可。
以上是理论理解部分,接下来上个🌰(例子),实战一下…
eg:
用二分法求方程 f(x) = x3 - x - 1 = 0 在区间[1,2]内的实根,要求精确到10-2,求一共需要多少次二分,并求出具有三位有效数的近似根。
有时候题目中也会说:要得到三位有效数字,意思是一样的,因为是三位有效数字,根的区间是(1,2),所以根的形式就是1.xxxxx,故根的第一位肯定不是0,所以要往小数点后面再数两位,最后确定根的形式就是1.xx,所以就有γ≤10-2。
解:
(1)首先,由于f(1)<0,f(2)>0,故在[1,2]内一定有一个根,又因为在区间[1,2]内f ’ (x)= 3x2-1>0,因此[1,2]区间内有且仅有一个实根。
根据公式:
(b - a)/ 2k+1 ≤ γ=10-2,
此时,a=1,b=2,所以代入之后就可以得到:
1/ 2k+1 ≤ 10-2
解出k=6,因此就意味着需要6次二分法。
求解过程如下图

(2)按照二分的步骤,比较f(x)的正负号可以可到如下图所示的过程:
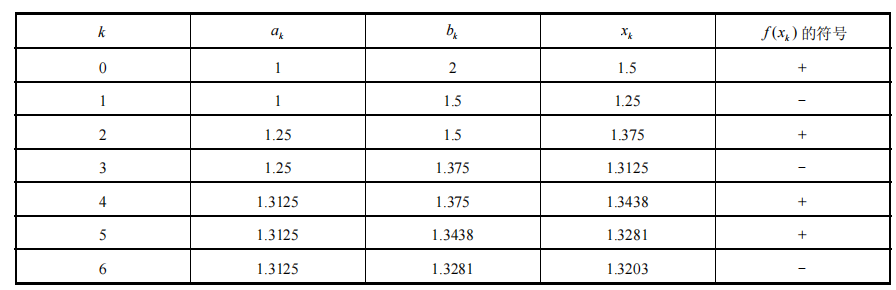
未完待更哦~~~
:)
