零基础-力扣100题从易到难详解（持续更新1-10题）

1.两数之和

思路：

题目的意思是在数组里找到两个不同位置的数（不存在多解），使它们相加等于target，返回它们的下标。

我们要做的就是遍历每个数，看看哪两个数能加成target，脑海里飘过三个方法：第一个是最复杂的暴力枚举写双层循环，两两相加，这里显然时间复杂度是下面说的“底线”O(n^2);第二个是哈希表，一边扫一边把值-下标存字典，查差值是否存在，时间复杂度为O(n)；第三种就是排序加双指针夹逼，但是会打乱原下标，需要额外的映射，属于比较炫技。

1.1暴力枚举（一些类知识）

class Solution(object):def twoSum(self,nums,target):#类内部声明的函数叫方法 python规定实例方法的第一个形参必须叫self 这个self代表将来调用该方法的那个对象本身，python解释器会自动把当前对象传进来
#在_init_里，self把值挂在当前这个对象自己身上，使之成为对象的一个属性，让后面任何地方都能通过这个对象访问它，要是没有赋值变量只能成为局部变量""":type nums: List[int]:type target: int:rtype: List[int]"""n = len(nums)#博主在这里做错了，tab对齐到def下面了for i in range(n-1):for j in range(i+1,n):if nums[i] + nums[j] == target:return[i,j]return []#return这里要对应n不是对应def

1.2Hash表

class Solution(object):def twoSum(self,nums,target):""":type nums: List[int]:type target: int:rtype: List[int]"""seen = {} #key : 存的是已经扫过的某个数，value：存的是这个数再nums的下标for idx,num in enumerate(nums):#用 enumerate 遍历 nums，每次拿到idx当前数字的下标，num当前数字的值，在这里相当于一个拆包语法need = target - numif need in seen:return [seen[need],idx]seen[num] = idx#如果 need 没找到，就把当前 num 记录到 seen 里，以备后面的数字来“配对”，这里num作为key，idx作为valuereturn []

1.3双指针（不建议）

class Solution(object):def twoSum(self, nums, target):""":type nums: List[int]:type target: int:rtype: List[int]"""# 把 (值, 原下标) 二元组保存下来再排序arr = [(num, i) for i, num in enumerate(nums)]arr.sort(key=lambda x: x[0])  # 按值升序left, right = 0, len(arr) - 1while left < right:s = arr[left][0] + arr[right][0]if s == target:return sorted([arr[left][1], arr[right][1]])elif s < target:left += 1else:right -= 1return []

2.有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 ：

输入：s = "([])"

输出：true

示例 ：

输入：s = "([)]"

输出：false

思路：在这道题中遍历或许不再是一个好方法，因为循环是不知道顺序的，对于这种有效且最近匹配的问题我们应该想到LIFO——last-in-first-out，因为后出现的左括号应该先被检查“闭合”。那我们思路就很明确了，当你读到）右括号的时候必须和最靠近它的上一个未匹配的（左括号匹配，再去看更外层的括号。

在操作上我们知道push(x) —— 把 x 放到最上面；pop() —— 拿走最上面的；top() —— 看一眼最上面是谁；is_empty() —— 栈里还有没有东西。对应在python里面就是用 list.append() 当 push，list.pop() 当 pop，list[-1] 当 top，not list 当 is_empty。

基础的操作就是遇到左括号把它push进栈等待匹配，遇到右括号就看栈顶top是不是对应左括号，是就可以pop完成匹配，否则非法输出错误，字符串扫完后栈为空则意味所有括号都匹配成功，要是不为空则说明左括号没有闭合。

记住：“需要最近配对、或撤销最近操作”的问题，十有八九都能用栈。

2.1经典栈（最优方法，代码好理解复杂度也不错）

遇到左括号就入栈，遇到右括号就看栈顶是否匹配，时间复杂度 O(n)，空间复杂度 O(n)。

class Solution(object):def isValid(self, s):""":type s: str:rtype: bool"""pair = {')':'(' , ']': '[', '}': '{'}#从左到右的查找，遇到右括号去匹配，所以写一个右括号匹配的字典stack = [] #创建栈for ch in s :if ch in pair:#右括号# 栈空或栈顶不匹配即为非法if not stack or stack[-1] != pair[ch]:return Falsestack.pop()#匹配成功弹出else:#左括号 这里记得写冒号，题主不太熟练写错了stack.append(ch)return  not stack

2.2栈+放哨兵（减少一次if判断 但是可读性比较差）

class Solution(object):def isValid(self, s):""":type s: str:rtype: bool"""pair = {')': '(', ']': '[', '}': '{'}stack = ['#']    # 不同之处在这里，放哨兵，保证 stack 永远不为空for ch in s:if ch in pair:if stack[-1] != pair[ch]:return Falsestack.pop()else:stack.append(ch)return len(stack) == 1 #只剩哨兵

2.3字符串替换（取巧的办法，面试慎用哦，而且每次扫描整串可能复杂度退到O（n^2））

通过不断把成对括号替换成空串，若最终能删光则合法：

class Solution(object):def isValid(self, s):""":type s: str:rtype: bool"""while '()' in s or '[]' in s or '{}'in s:s = s.replace('()','').replace('[]','').replace('{}','')return s == ''

很凑巧的是最近匹配的LIFO顺序，replace的扫描方向也可以满足这一点：

str.replace(old, new) 的作用从左到右一次性扫描整个字符串，把所有与 old 不重叠 的子串替换成 new。

3.合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

示例 1：

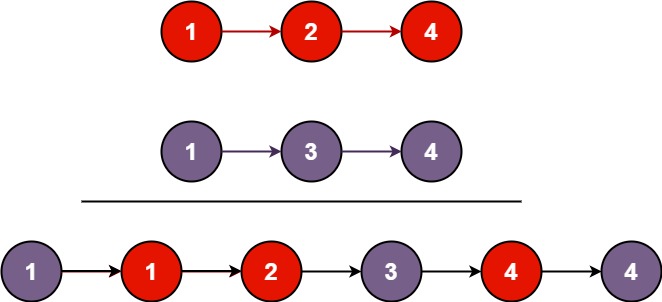
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

思路：好像没啥好说的，学过C艹链表肯定都做过这种题，因为是零基础就重新把链表讲一遍吧。

3.1哑结点+迭代（最常用，面试首选，时间 O(n+m)，空间 O(1)）

用哑结点简化边界处理，两个指针分别扫描 l1、l2，每次把较小的节点接到新链表尾部。

# Definition for singly-linked list.
# class ListNode(object):#已经预先定义好了
#     def __init__(self, val=0, next=None):
#         self.val = val#用来存数字
#         self.next = next#存下一间房 如果None则表示后面没有了class Solution(object):def mergeTwoLists(self, l1, l2):""":type l1: ListNode:type l2: ListNode:rtype: ListNode"""dummy = ListNode(0)  #哑结点 值是多少无所谓 因为我们不知道真正的头是谁 干脆直接放一个空节点占住这个坑tail = dummy# tail永远指向“当前链表的最后一个节点”， 负责把较小的节点“挂到自己屁股后面”。while l1 and l2:#循环比较和挂链if l1.val <= l2.val:#左边更小tail.next = l1#l1挂到链表尾巴l1 = l1.next#l1更近一步else:#右边更小tail.next = l2#同理l2挂到链表尾巴l2 = l2.nexttail = tail.next#tail也前进一步#把剩余部分一次挂上去tail.next = l1 if l1 else 12 return dummy.next#返回真正头节点 dummy 只是个占位符，它的 next 才是合并后真正的头：

3.2递归（代码短，但栈深O（n+m））

用哑结点简化边界处理，两个指针分别扫描l1、l2，每次把较小的节点接到新链表尾部。

class Solution(object):def mergeTwoLists(self, l1, l2):""":type l1: ListNode:type l2: ListNode:rtype: ListNode"""if not l1:#这两段代码是说如果有一条链表为空，则直接返回另外一条return l2if not l2:return l1if l1.val <= l2.val:#谁小谁当头节点，剩下的继续递归合并l1.next = self.mergeTwoLists(l1.next, l2)return l1else:l2.next = self.mergeTwoLists(l1, l2.next)return l2

这个思路能理解但是比较难思考,首先先比两链表头谁小，就把这个节点留下，然后递归地合并剩下的两条链表，再把结果挂到当前节点的next。那么这样递归下去就是一直有最小的留下

3.3利用优先队列（堆）扩展思路（可一次合并 k 条链表）进阶

把链表头节点放入最小堆，每次弹出最小值节点，再把它的next压回堆，直到堆空。

链表 l1: 1→2→4
链表 l2: 1→3→4
桶初始：[(1,l1), (1,l2)]   # 两个 1第 1 次 pop：1(l1)  → 结果链表 1把 l1.next=2 入桶 → [(1,l2), (2,l1)]第 2 次 pop：1(l2)  → 结果链表 1→1把 l2.next=3 入桶 → [(2,l1), (3,l2)]第 3 次 pop：2(l1)  → 结果链表 1→1→2把 l1.next=4 入桶 → [(3,l2), (4,l1)]...依次下去，桶里永远保持【最小值在顶端】

为什么要用这个方法因为最小堆会自动重新排好顺序，下一次还是给我们当前最小的节点。

import heapq#heapq就是一个魔法桶，你往里面扔数字，他永远把最小的数字放到最上面，最小堆（min-heap）
#把节点扔进同：heapq.heappush(heap, (node.val, node))
#从桶顶拿最小：val, node = heapq.heappop(heap)
#把拿出的节点next继续扔进桶：if node.next: heappush(...)class Solution(object):def mergeTwoLists(self, l1, l2):""":type l1: ListNode:type l2: ListNode:rtype: ListNode"""# Python 的堆需要可比较对象，这里用 tuple(val, node)heap = []#1.先造个空链表if l1:   #如果 l1 不是空链表，就把 (值, 节点本身) 这个小包裹扔进桶heapq.heappush(heap, (l1.val, l1))if l2:   #同理，把 l2 的头节点也扔进去heapq.heappush(heap, (l2.val, l2))#桶会自动按第一个数字（值）排序，最小的排在最上面。dummy = ListNode(0)  # 哑结点tail = dummywhile heap:#heap里面已经有了两个包裹，循环开始val, node = heapq.heappop(heap)  # 最小节点tail.next = nodetail = tail.next# 如果该节点后面还有，继续入堆if node.next:heapq.heappush(heap, (node.next.val, node.next))#继续往桶里扔东西return dummy.next