DAY 58 经典时序预测模型2
知识点回顾:
- 时序建模的流程
- 时序任务经典单变量数据集
- ARIMA(p,d,q)模型实战
- SARIMA摘要图的理解
- 处理不平稳的2种差分
- n阶差分---处理趋势
- 季节性差分---处理季节性
昨天我们掌握了AR, MA, 和 ARMA 模型,它们是处理平稳时间序列的利器。但现实世界的数据,比如股票价格、公司销售额,往往带有明显的趋势性或季节性,它们是不平稳的。今天,我们就来学习ARIMA模型,它正是为了解决这个问题而生的。
他进一步引入差分来解决不平稳问题
差分是使数据平稳化的关键步骤。
一阶差分: 就是序列中每个点减去它前一个点的值。
diff(t) = value(t) - value(t-1)
这通常可以消除数据中的线性趋势。
二阶差分: 对一阶差分后的结果再做一次差分。
diff2(t) = diff(t) - diff(t-1)
这可以消除数据中的曲线趋势(比如抛物线趋势)。
ARIMA建模的完整流程
建立一个ARIMA模型,通常遵循以下步骤:
- 数据可视化:观察原始时间序列图,判断是否存在趋势或季节性。
- 平稳性检验:
- 对原始序列进行ADF检验。
- 如果p值 > 0.05,说明序列非平稳,需要进行差分。
- 确定差分次数 d:
- 进行一阶差分,然后再次进行ADF检验。
- 如果平稳了,则 d=1。否则,继续差分,直到平稳。
- 确定 p 和 q:
- 对差分后的平稳序列绘制ACF和PACF图。
- 根据昨天学习的规则(PACF定p,ACF定q)来选择p和q的值。
- 建立并训练ARIMA(p, d, q)模型。
- 模型评估与诊断:查看模型的摘要信息,检查残差是否为白噪声。
- 进行预测
一、 时序任务经典数据集
就像机器学习有鸢尾花、手写数字、波士顿房价这些“标准”数据集一样,时间序列分析领域也有一些“名人堂”成员。
这些经典数据集之所以经典,是因为它们各自清晰地展示了时间序列中一种或多种核心特征(如趋势、季节性、周期性等),非常适合用来教学和检验模型。
下面介绍几个最著名、最常用的单变量时间序列经典数据集,并附上获取它们的代码。
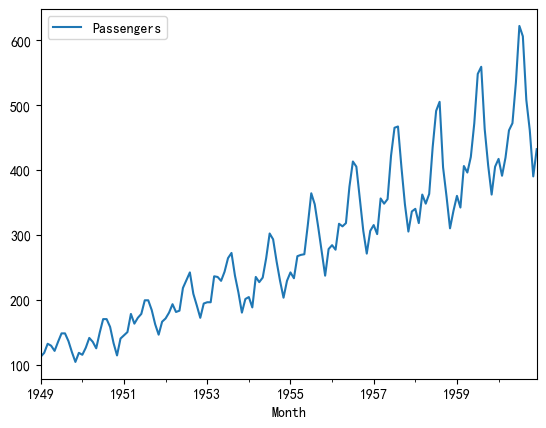
1.1 国际航空乘客数量 (Airline Passengers)
- 数据描述: 1949年到1960年每月国际航空公司的总乘客数量。
- 强趋势性: 随着时间推移,乘客数量有非常明显的线性增长趋势。
- 强季节性: 每年都有一个固定的模式,夏季(6-8月)是高峰,冬季是低谷。
- 变化的方差: 越到后期,季节性波动的幅度越大,这是一种异方差性。
import pandas as pd
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv'
df_air = pd.read_csv(url, header=0, index_col=0, parse_dates=True)
df_air.head()# 这是一种直接使用 URL 在线读取数据集的方式,代码通过pd.read_csv(url)直接从网络 URL 读取数据,Pandas 会自动处理网络请求并加载数据到内存中,属于 “在线读取” 方式。df_air.plot()# <matplotlib.axes._subplots.AxesSubplot at 0x29eb6ea3e80>| Passengers | |
|---|---|
| Month | |
| 1949-01-01 | 112 |
| 1949-02-01 | 118 |
| 1949-03-01 | 132 |
| 1949-04-01 | 129 |
| 1949-05-01 | 121 |
这里没有导入matplotlib仍然可以画图,是因为当调用df.plot()时,Pandas 会隐式导入 Matplotlib(如果尚未导入),并使用其绘图接口生成图表。对于简单的可视化需求,无需显式导入 Matplotlib,减少代码量。这里省略了plt.title(‘xxx’)和plt.show()等
1.2 太阳黑子数量 (Sunspots)
- 数据描述: 每年观测到的太阳黑子数量。
- 无明显趋势: 长期来看,数据没有持续的上升或下降趋势。
- 强周期性 (Cyclical): 数据呈现非常明显的周期性波动,大约每11年一个周期。注意,这与“季节性”不同,季节性周期是固定的(如12个月),而这里的周期长度是近似的。
- 相对平稳: 经过检验,数据通常被认为是平稳或近似平稳的。
from statsmodels.datasets import sunspots
df_sun = sunspots.load_pandas().data['SUNACTIVITY']
df_sun.head()# 0 5.0
# 1 11.0
# 2 16.0
# 3 23.0
# 4 36.0
# Name: SUNACTIVITY, dtype: float64df_sun.plot()# <matplotlib.axes._subplots.AxesSubplot at 0x29eb29bde80>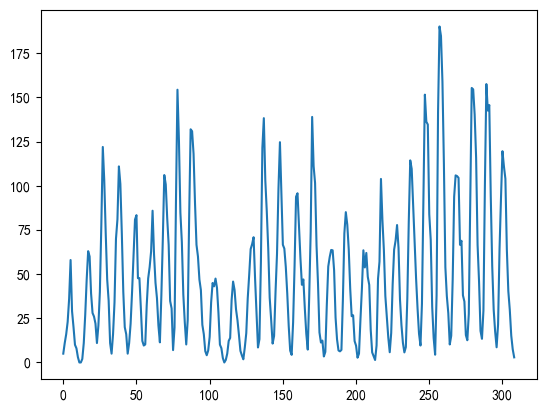
非常适合用来理解ARMA模型。由于数据本身比较平稳,不需要差分,可以专注于用ACF和PACF图来确定 p 和 q 的值。
1.3 加州每日女性出生数量 (Daily Female Births)
- 数据描述: 1959年,美国加州每一天的女性新生儿数量。
- 无趋势、无季节性: 数据看起来像随机波动,没有明显的趋势或可预测的季节模式。
- 平稳性: ADF检验通常会显示该序列是平稳的。
import pandas as pd
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-total-female-births.csv'
df_births = pd.read_csv(url, header=0, index_col=0, parse_dates=True)
# df_births.plot()
df_births.plot()# <matplotlib.axes._subplots.AxesSubplot at 0x29eb6fede80>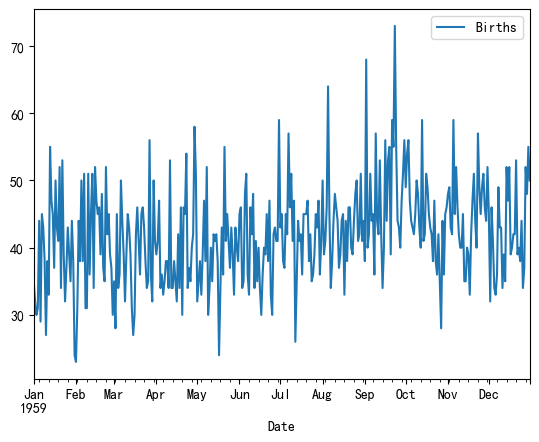
二、时间序列任务实战
进阶: 使用 太阳黑子 数据,让学员练习用ACF/PACF为ARMA模型定阶。
核心: 用 国际航空乘客 数据,系统地讲解从非平稳到平稳(差分),再到建立ARIMA和SARIMA的全过程。
2.1 加州每日女性预测
# 导入必要的库
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA# 设置matplotlib以正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 加载数据
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-total-female-births.csv'
df = pd.read_csv(url, header=0, index_col=0, parse_dates=True)
df.columns = ['Births']
ts_data = df['Births']print("--- 原始数据预览 ---")
print(ts_data.head())# 绘制时序图
plt.figure(figsize=(14, 7))
plt.plot(ts_data)
plt.title('1959年加州每日女性出生数量')
plt.xlabel('日期')
plt.ylabel('出生数量')
plt.show()#--- 原始数据预览 ---
# Date
# 1959-01-01 35
# 1959-01-02 32
# 1959-01-03 30
# 1959-01-04 31
# 1959-01-05 44
# Name: Births, dtype: int64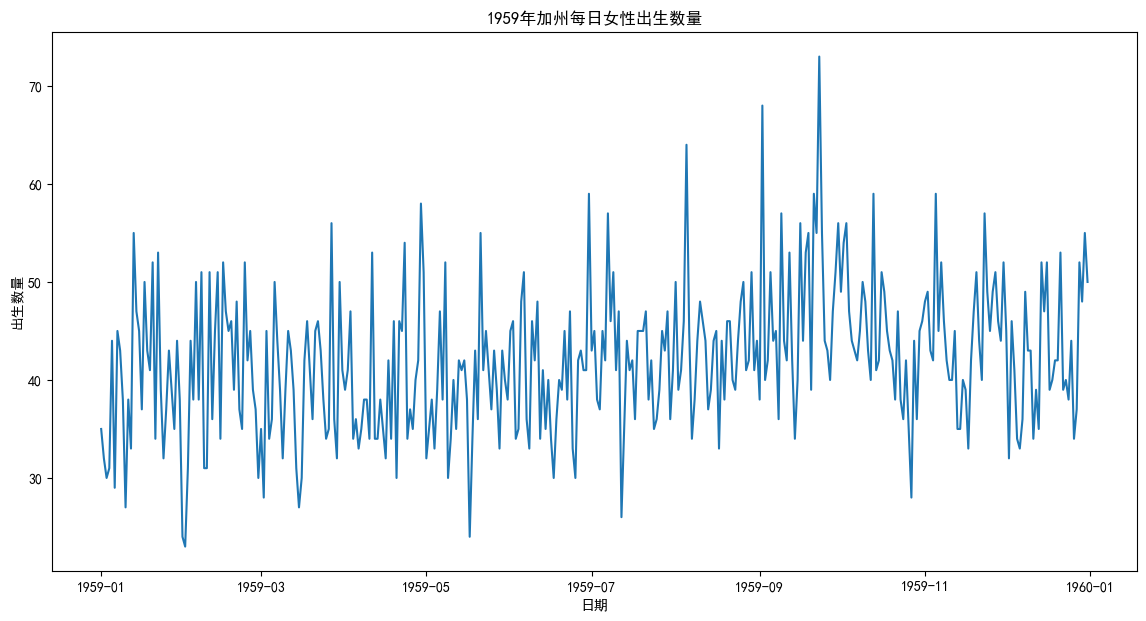
从图上看,数据点在一个稳定的水平线(大约40)上下随机波动。没有明显的上升或下降趋势,也没有看到以周或月为单位的固定模式。这给我们一个初步印象:这个序列很可能是平稳的。
直觉需要被验证。我们使用ADF检验来科学地判断其平稳性。
def adf_test(timeseries):print('--- ADF检验结果 ---')# H0: 序列非平稳; H1: 序列平稳result = adfuller(timeseries)print(f'ADF Statistic: {result[0]}')print(f'p-value: {result[1]}') # 重点关注这个值if result[1] <= 0.05:print("结论: 成功拒绝原假设,序列是平稳的。")else:print("结论: 未能拒绝原假设,序列是非平稳的。")adf_test(ts_data)# --- ADF检验结果 ---
# ADF Statistic: -4.808291253559765
# p-value: 5.2434129901498554e-05
# 结论: 成功拒绝原假设,序列是平稳的。既然数据是平稳的,我们就不需要对它进行差分来“铲平”它。这意味着:差分次数 d = 0
我们现在只需要确定 p 和 q。模型将是 ARIMA(p, 0, q),这其实就是我们昨天学的 ARMA(p, q) 模型。
# 因为数据是平稳的,我们直接对原始数据绘制ACF和PACF
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))plot_acf(ts_data, ax=ax1, lags=40)
ax1.set_title('自相关函数 (ACF)')plot_pacf(ts_data, ax=ax2, lags=40)
ax2.set_title('偏自相关函数 (PACF)')plt.tight_layout()
plt.show()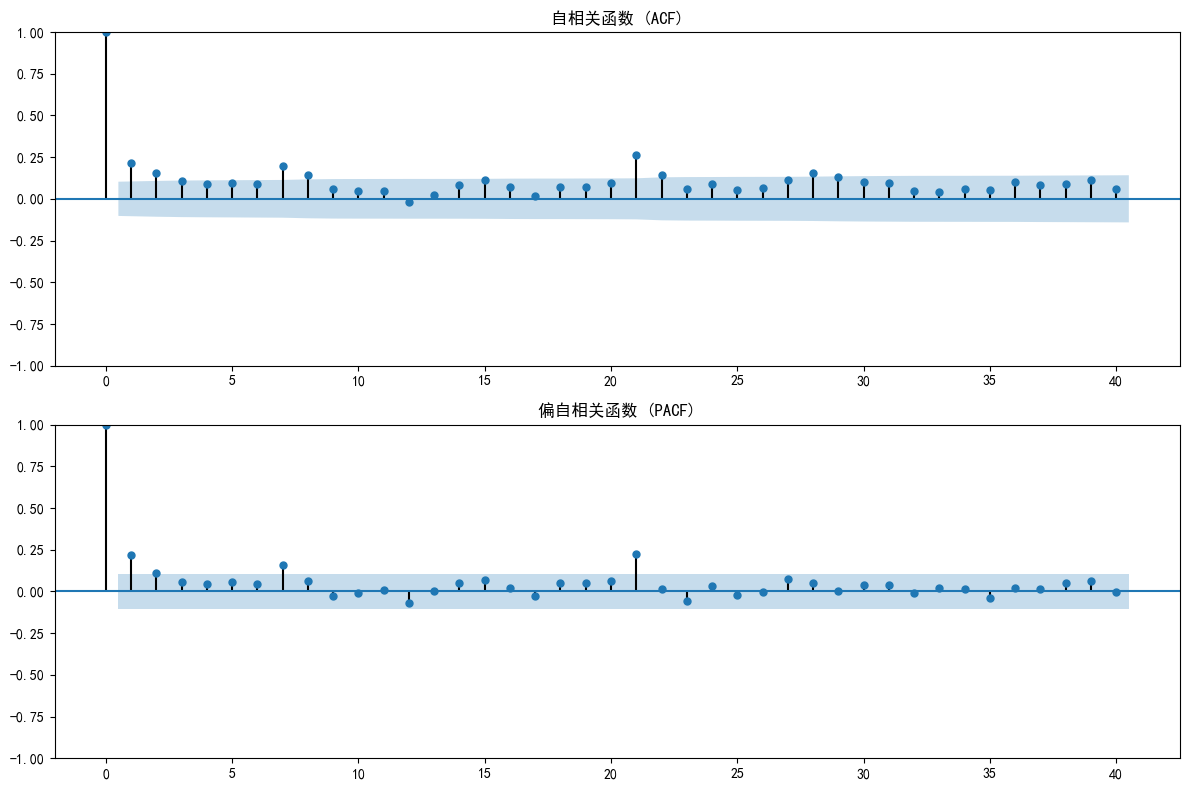
- PACF图: 在滞后2阶之后,几乎所有的相关性都落入了蓝色置信区间内,我们可以认为它在 滞后2阶后截尾。这强烈暗示 p=2。
- ACF图: 呈现出拖尾的模式(缓慢下降)。
所以,我们的候选模型是 ARIMA(2, 0, 0)。
import warnings
warnings.filterwarnings("ignore")
# 建立ARIMA(2, 0, 0)模型
model = ARIMA(ts_data, order=(2, 0, 0))
arima_result = model.fit()# 打印模型摘要
print(arima_result.summary())# 让我们预测未来30天
forecast_steps = 30
forecast = arima_result.get_forecast(steps=forecast_steps)
pred_mean = forecast.predicted_mean
conf_int = forecast.conf_int()# 绘制结果
plt.figure(figsize=(14, 7))
plt.plot(ts_data, label='原始数据')
# 绘制模型在历史数据上的拟合值
plt.plot(arima_result.fittedvalues, color='orange', label='模型拟合值')
# 绘制未来预测值
plt.plot(pred_mean, color='red', label='未来预测值')
# 绘制置信区间
plt.fill_between(conf_int.index,conf_int.iloc[:, 0],conf_int.iloc[:, 1], color='pink', alpha=0.5, label='95%置信区间')
plt.title('ARIMA(2,0,0)模型拟合与预测')
plt.legend()
plt.show() SARIMAX Results
==============================================================================
Dep. Variable: Births No. Observations: 365
Model: ARIMA(2, 0, 0) Log Likelihood -1234.182
Date: Sun, 29 Jun 2025 AIC 2476.364
Time: 16:08:32 BIC 2491.963
Sample: 01-01-1959 HQIC 2482.563- 12-31-1959
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 41.9816 0.568 73.885 0.000 40.868 43.095
ar.L1 0.1939 0.055 3.544 0.000 0.087 0.301
ar.L2 0.1139 0.055 2.070 0.038 0.006 0.222
sigma2 50.6301 3.527 14.354 0.000 43.717 57.544
===================================================================================
Ljung-Box (L1) (Q): 0.02 Jarque-Bera (JB): 18.89
Prob(Q): 0.89 Prob(JB): 0.00
Heteroskedasticity (H): 0.96 Skew: 0.48
Prob(H) (two-sided): 0.83 Kurtosis: 3.57
===================================================================================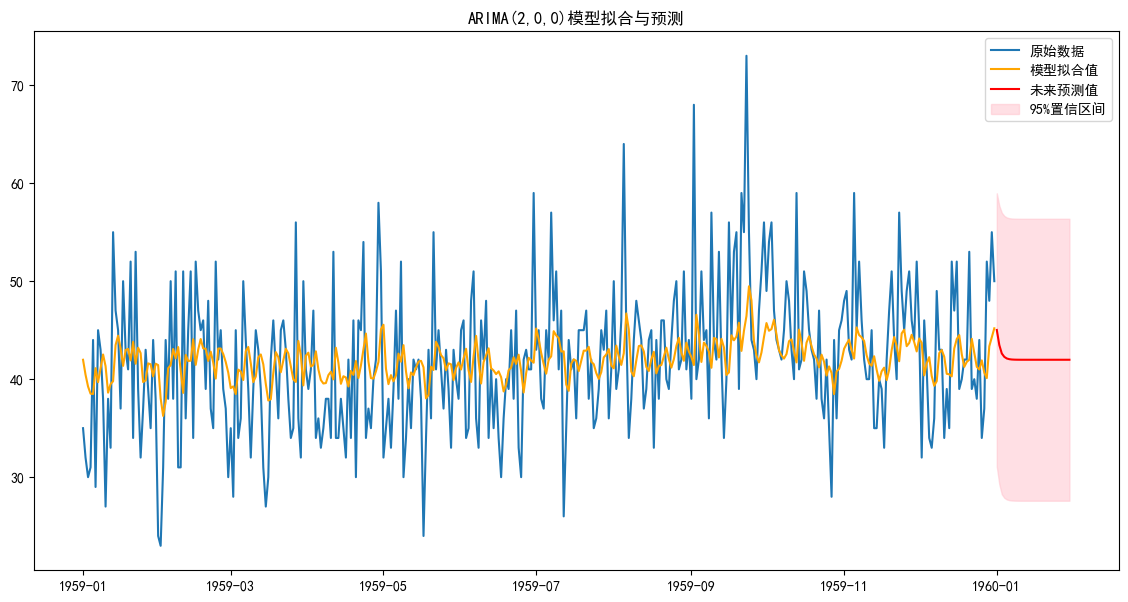
从视觉上看,这个模型的拟合效果确实很差。橙色的“模型拟合值”线非常平滑,完全没有捕捉到蓝色“原始数据”那些剧烈的峰值和谷值。
那么,为什么一个在统计上“通过检验”的模型,看起来却这么“糟糕”呢?从视觉上看,这个模型的拟合效果确实很差。橙色的“模型拟合值”线非常平滑,完全没有捕捉到蓝色“原始数据”那些剧烈的峰值和谷值。
那么,为什么一个在统计上“通过检验”的模型,看起来却这么“糟糕”呢?
“每日女性出生数量”这个数据集,其内在的随机性(我们称之为“噪音”)非常高。今天比昨天多生了10个孩子,明天又比今天少生了8个,这其中大部分是无法预测的随机事件。
然而,在这个巨大的随机噪音之下,隐藏着一个非常微弱的模式。我们的ARIMA(2,0,0)模型和统计检验发现:今天的出生人数,与昨天(ar.L1)和前天(ar.L2)的出生人数,存在一点点微弱但统计上显著的自相关关系。ARIMA模型就像一个筛子,它的任务是从混杂着沙子(噪音)和金子(模式)的混合物中,把“金子”给筛出来。
- 橙色线(模型拟合值):这就是模型筛出来的“金子”。它是基于前两天数据计算出的期望值或预测值。因为模式本身是平滑的(只是一个微弱的自相关),所以这条线必然是平滑的。它代表了数据中可预测的部分。
- 蓝色线与橙色线的差距(残差):这就是被模型筛掉的“沙子”,也就是噪音。这是模型认为不可预测的随机部分。
想象一下,如果我们强行建立一个能完美追踪每一个蓝色数据点的模型。这条橙色线会和蓝色线完全重合。这看起来是不是“拟合得很好”?但这恰恰是“过拟合”(Overfitting)!
这个模型把所有的“噪音”都当成了“模式”来学习。当让它去预测未来时,它会因为学了太多随机噪音而做出非常离谱和不稳定的预测。
一个好的模型,懂“断舍离”——它只学习真正的模式,并勇敢地承认:“剩下的部分,我无法预测,因为它们是随机的。”这就是我们在模型摘要中做的Ljung-Box检验。Prob(Q) = 0.89,这个值远大于0.05。它的意思是:“我们非常有把握地认为,这些残差是纯粹的随机噪音,里面已经没有任何模式可供提取了。”
在时间序列分析中,我们的目标不是创造一个能“复制”历史的“复印机”(过拟合),而是要打造一个能“理解”历史规律的“侦探”(好模型)。这个“侦探”能区分出哪些是线索(模式),哪些是干扰项(噪音)。因此,一个好的模型的残差,必须像白噪音一样“无聊”和“不可预测”。这正是我们在这个例子中看到的。
现在我们来解读下这个输出的表
先看表头,SARIMAX Results
在 statsmodels 库的现代版本中,ARIMA、SARIMA 和 SARIMAX 的后端实现被统一到了一个强大的 SARIMAX 类中。你可以把它理解成一个“全能型”模型引擎。所以结果显示 SARIMAX Results
SARIMAX 是 Seasonal AutoRegressive Integrated Moving Average with eXogenous regressors 的缩写。它是最通用的模型,包含了:
- ARIMA(p,d,q): 非季节性部分。
- Seasonal(P,D,Q,m): 季节性部分。
- eXogenous(X): 外部变量(例如,用天气温度来预测冰淇淋销量)。
简单来说:ARIMA 是 SARIMAX 的一个特例。
然后看第二部分
这是模型的核心参数部分,告诉我们模型具体学到了什么。
-
coef (系数): 这是模型计算出的每个参数的值。
- const: 常数项/截距。可以理解为序列的基准水平或均值,这里是 41.98,和我们之前图上看到的均值差不多。
- ar.L1: 滞后1阶的自回归项 (AR) 系数 φ₁。值为 0.1939。
- ar.L2: 滞后2阶的自回归项 (AR) 系数 φ₂。值为 0.1139。
- sigma2: 模型残差的方差。值越小说明模型的拟合误差越小。
-
P>|z| (p值): 这是最重要的列! 它检验的是“该系数是否显著不为0”。判断标准: 如果 p值 < 0.05,我们就可以认为这个系数是统计上显著的,它对模型是有贡献的。
- const 的 p值为 0.000,非常显著。
- ar.L1 的 p值为 0.000,非常显著。
- ar.L2 的 p值为 0.038,小于0.05,也是显著的。
在理解上述参数后,此时还有标准差和置信区间这2个参数。
coef 列的值,比如 ar.L1 的 0.1939,是模型通过计算得出的 最有可能的、最佳的估计值。std err(标准误差)衡量的是 系数估计值的不确定性或“抖动幅度”。std err 越小,说明我们的估计越精确、越稳定。如果换一份数据,估计出的系数也不会跑偏太远。这就像一个经验丰富的射手,每次射击都紧紧围绕靶心。std err 是 0.055。这是一个相对较小的值,表明对 0.1939 这个估计是比较有信心的。
[0.087 0.301] 是 ar.L1 系数的 95%置信区间。它的含义是:我们有95%的信心相信,ar.L1 这个参数 真正的、未知的值 落在这个区间之内。我们的最佳估计值 0.1939 只是这个区间中的一个点(通常是中心点)。真实的参数值可能比它大一点,也可能小一点,但很大概率不会超出 [0.087, 0.301] 这个范围。此外,如果置信区间完全不包含0 (像这里的 [0.087, 0.301]),就说明我们有95%的信心断定,这个系数的真实值不是0。这等价于p值小于0.05,即系数是显著的。如果置信区间包含了0 (例如,[-0.1, 0.2]),那就意味着0是一个可能的真实值。我们无法排除“这个系数其实是0,对模型没有作用”的可能性。这等价于p值大于0.05,即系数是不显著的。这2个判断方法是等价的。
结论: 我们选择的 p=2 是合理的,因为两个AR项都是显著的。
第三部分:残差诊断检验
好的残差:应该是模型“吃剩下的、完全没有营养的、随机的白噪声(White Noise)”。如果还剩下隐藏的线索(非白噪声) -> 说明侦探有疏漏,模型还有改进空间。
白噪声的要求:
- 无自相关
- 方差恒定–如果方差不恒定(比如,越到近期,误差波动越大),说明你的模型在某些时期的预测能力很不可靠。这会影响你对未来预测不确定性的估计。残差随时间变化的图应该像一条宽度稳定的“带子”,而不是一个“喇叭口”或“纺锤”。在检验上对应着:异方差性检验 (Heteroskedasticity test) 的p值应大于0.05。
- 均值为0–避免系统性偏差
锦上添花的附加条件:服从正态分布,它主要用于构建准确的预测区间 (Prediction Intervals)。如果残差是正态的,我们就能更有信心地说“未来的值有95%的概率落在某个区间内”。
2.2 国际航空乘客数量实战
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import warningswarnings.filterwarnings("ignore") # 忽略一些模型拟合时产生的警告信息
# 加载数据
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv'
df_air = pd.read_csv(url, header=0, index_col=0, parse_dates=True)
df_air.rename(columns={'#Passengers': 'Passengers'}, inplace=True) # 列名简化# 绘制原始数据
plt.figure(figsize=(12, 6))
plt.plot(df_air['Passengers'])
plt.title('Airline Passengers (1949-1960)')
plt.xlabel('Year')
plt.ylabel('Number of Passengers')
plt.grid(True)
plt.show()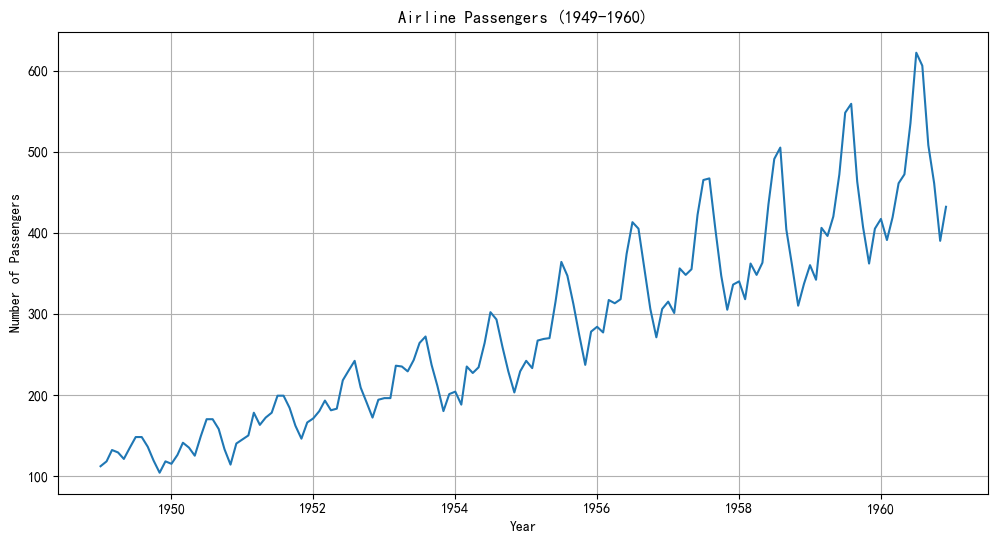
arima无法处理季节性(没有内置季节性差分,只有n阶差分),所以需要先手动处理季节性。
能看到季节性的幅度越来越大,这是一种乘性效应。对数变换是处理这种情况的标准方法,它可以将乘性关系变为加性关系,从而稳定方差。
# 对数变换
df_air['log_passengers'] = np.log(df_air['Passengers'])plt.figure(figsize=(12, 5))
plt.plot(df_air['log_passengers'])
plt.title('Log-Transformed Airline Passengers')
plt.grid(True)
plt.show()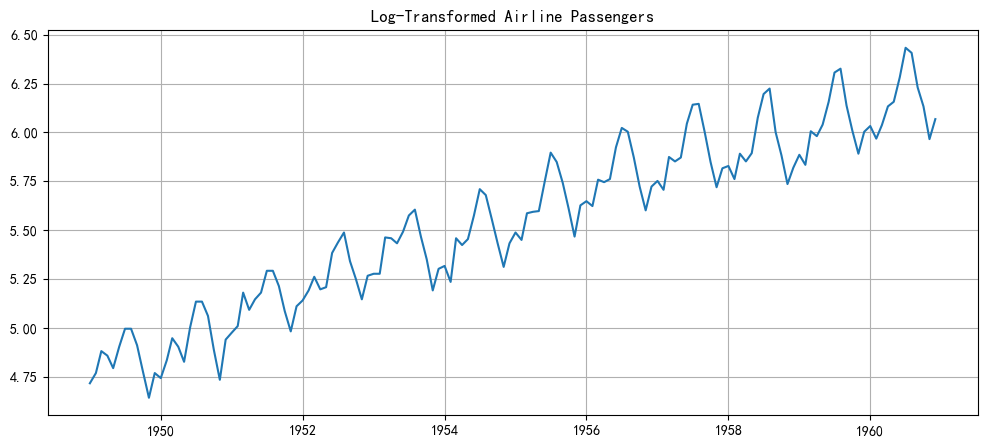
现在,波动的幅度看起来稳定多了,但趋势和季节性依然存在。
# 季节性差分 (m=12)
df_air['log_seasonal_diff'] = df_air['log_passengers'].diff(12)# 丢掉因差分产生的NaN值
deseasonalized_data = df_air['log_seasonal_diff'].dropna()plt.figure(figsize=(12, 5))
plt.plot(deseasonalized_data)
plt.title('Deseasonalized and Log-Transformed Data')
plt.grid(True)
plt.show()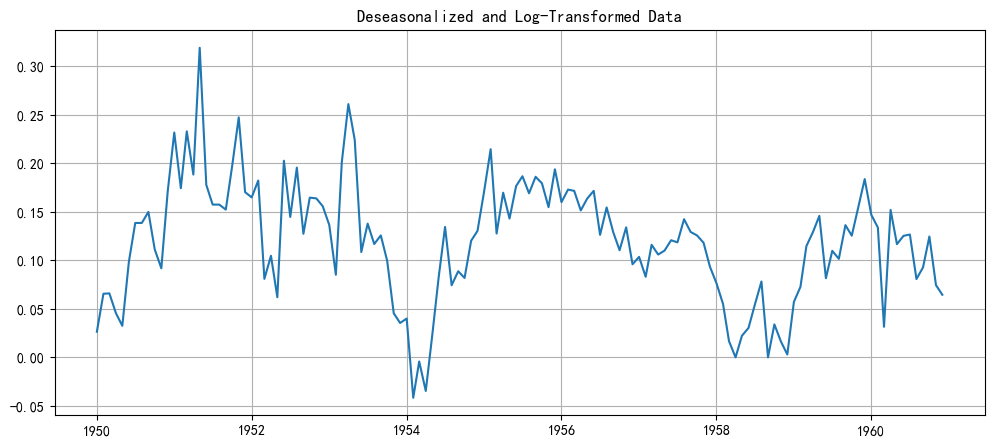
我们成功地去除了季节性模式。现在的数据看起来就像一个有线性趋势的普通时间序列。这种数据正是标准ARIMA模型擅长处理的。
现在,我们为这个 deseasonalized_data 序列选择 (p, d, q) 参数
确定d(差分阶数): 从上图看,数据仍然有明显的上升趋势,所以它不是平稳的。我们需要进行一阶差分来消除这个趋势。因此,d=1。
确定p和q: 我们对差分一次后的序列绘制ACF和PACF图来确定 p 和 q。
# 对去季节性的数据再进行一阶差分,使其平稳
stationary_data = deseasonalized_data.diff(1).dropna()# 绘制ACF和PACF图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))
plot_acf(stationary_data, lags=24, ax=ax1)
plot_pacf(stationary_data, lags=24, ax=ax2)
plt.show()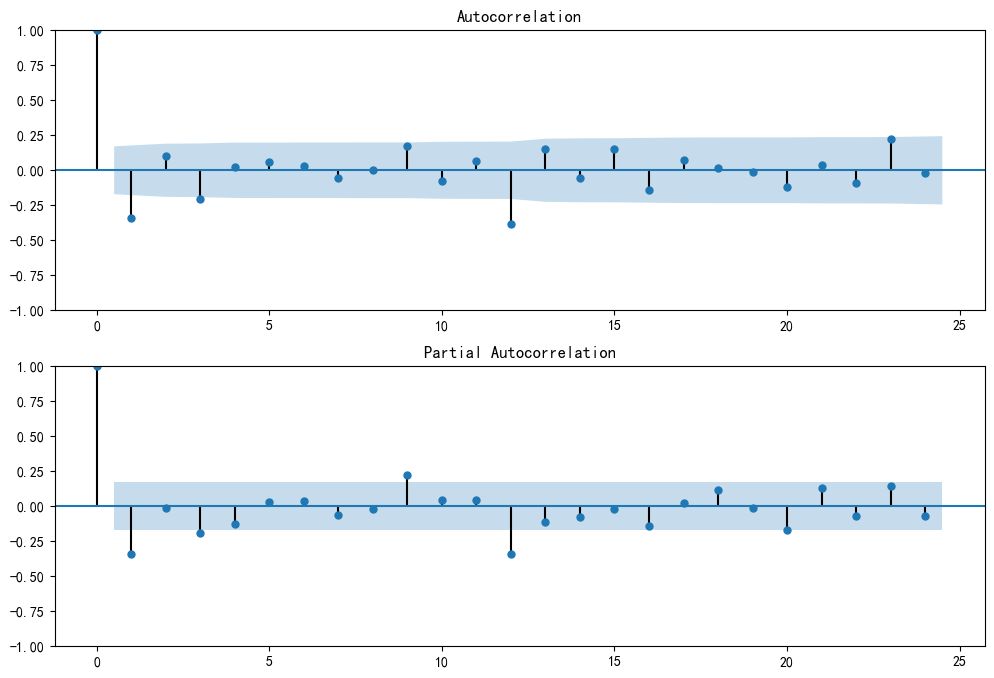
PACF图: 在滞后1阶后迅速截尾(降到置信区间内)。这强烈暗示 p=1。
ACF图: 在滞后1阶后也迅速截尾。这强烈暗示 q=1。
因此,我们为这个预处理后的数据选择的模型是 ARIMA(1, 1, 1)。
ps:这里其实可以看到在12阶的时候超出了置信区间,实际上这个尖峰是残余的季节性信号。即使我们已经做了一次季节性差分 (.diff(12)),数据中仍然保留着一些与12个月前相关的模式。换句话-说,我们手动进行的季节性差分并没有100%完全地消除季节性影响。
我们将使用数据的前11年(到1959年底)作为训练集,最后1年(1960年)作为测试集来验证我们的预测。
from statsmodels.tsa.arima.model import ARIMA# 准备训练数据(经过预处理的)
# 注意:我们是对去季节性的数据进行建模
train_data = deseasonalized_data[:'1959']# 定义并拟合ARIMA(1,1,1)模型
model = ARIMA(train_data, order=(1, 1, 1))
model_fit = model.fit()print(model_fit.summary())# 预测未来12个点(1960年全年)
# 模型预测的是经过变换后的数据
forecast_diff = model_fit.forecast(steps=12) SARIMAX Results
==============================================================================
Dep. Variable: log_seasonal_diff No. Observations: 120
Model: ARIMA(1, 1, 1) Log Likelihood 206.898
Date: Sun, 29 Jun 2025 AIC -407.797
Time: 16:08:33 BIC -399.459
Sample: 01-01-1950 HQIC -404.411- 12-01-1959
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.5365 0.260 -2.062 0.039 -1.046 -0.027
ma.L1 0.2535 0.300 0.844 0.399 -0.335 0.842
sigma2 0.0018 0.000 9.171 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 4.07
Prob(Q): 0.84 Prob(JB): 0.13
Heteroskedasticity (H): 0.24 Skew: 0.05
Prob(H) (two-sided): 0.00 Kurtosis: 3.90
===================================================================================可以看到,这里ma(1)不显著,所以q=0 ,我们应该尝试一个更简单的模型:ARIMA(1, 1, 0)。
# 重新拟合一个更简单的模型 ARIMA(1, 1, 0)
model_simplified = ARIMA(train_data, order=(1, 1, 0))
model_fit_simplified = model_simplified.fit()
print(model_fit_simplified.summary())# 比较两个模型的AIC
# 原模型 ARIMA(1,1,1) 的 AIC: -407.797
# 简化模型 ARIMA(1,1,0) 的 AIC 会是多少?
# (运行代码后,ARIMA(1,1,0)的AIC大约是-408.8,比-407.797更小) SARIMAX Results
==============================================================================
Dep. Variable: log_seasonal_diff No. Observations: 120
Model: ARIMA(1, 1, 0) Log Likelihood 206.811
Date: Sun, 29 Jun 2025 AIC -409.622
Time: 16:08:33 BIC -404.064
Sample: 01-01-1950 HQIC -407.365- 12-01-1959
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.3174 0.068 -4.641 0.000 -0.451 -0.183
sigma2 0.0018 0.000 9.274 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 4.19
Prob(Q): 0.99 Prob(JB): 0.12
Heteroskedasticity (H): 0.25 Skew: 0.12
Prob(H) (two-sided): 0.00 Kurtosis: 3.89
===================================================================================AIC是一个权衡模型拟合优度和复杂度的指标,AIC值越小,模型通常越好。
可以看到,ARIMA(1,1,0)的AIC大约是-408.8,比 ARIMA(1, 1, 1)的-407.797更小。
现在我们得到了12个预测值 forecast_diff,但这些值是“经过对数变换、季节性差分和一阶差分”后的值。我们需要一步步把它还原回去。这个过程比较繁琐,是手动处理季节性的最大难点。
# 让我们给变量取个更准确的名字
# forecast_deseasonalized 是对“去季节性”序列的直接预测
forecast_deseasonalized = model_fit.forecast(steps=12)# 逆向变换过程
predictions = []# 逐步还原预测值
for i in range(len(forecast_deseasonalized)):# 1. 还原季节性差分 (直接使用预测值)# log(y_t) = y'_t + log(y_{t-12})# y'_t 就是 forecast_deseasonalized[i]# 获取12个月前的历史对数值last_year_log_val = df_air['log_passengers']['1959'].iloc[i]# 加上历史值,得到预测的对数值pred_log = forecast_deseasonalized.iloc[i] + last_year_log_val# 2. 还原对数变换 (exp)pred_original_scale = np.exp(pred_log)predictions.append(pred_original_scale)# 将预测结果转换为Series,方便绘图
# 注意:forecast_deseasonalized 自带了正确的日期索引,可以直接使用
predictions_series = pd.Series(predictions, index=forecast_deseasonalized.index)# --- 重新绘图 ---
plt.figure(figsize=(14, 7))
# 原始数据
plt.plot(df_air['Passengers'], label='Original Data')
# 我们的预测
plt.plot(predictions_series, color='red', linestyle='--', label='ARIMA Forecast (Corrected)')
plt.title('Airline Passengers Forecast using Manual Preprocessing + ARIMA')
plt.xlabel('Year')
plt.ylabel('Number of Passengers')
plt.legend()
plt.grid(True)
plt.show()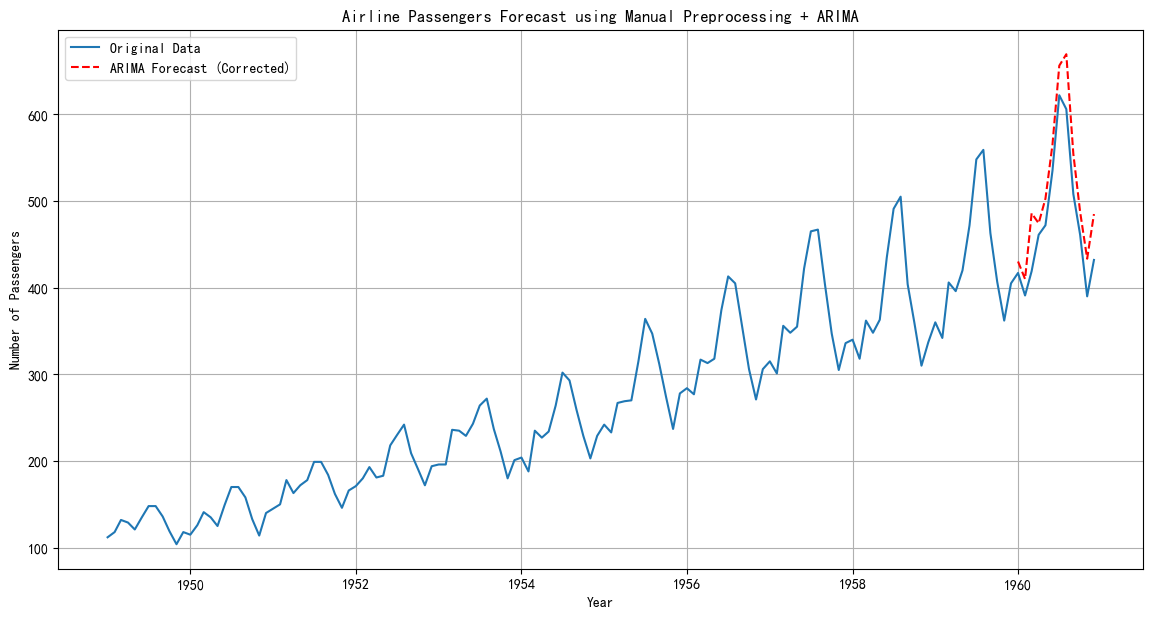
时间序列建模的迭代过程:初步选择 -> 拟合检验 -> 模型修正 -> 数据还原。
@浙大疏锦行
