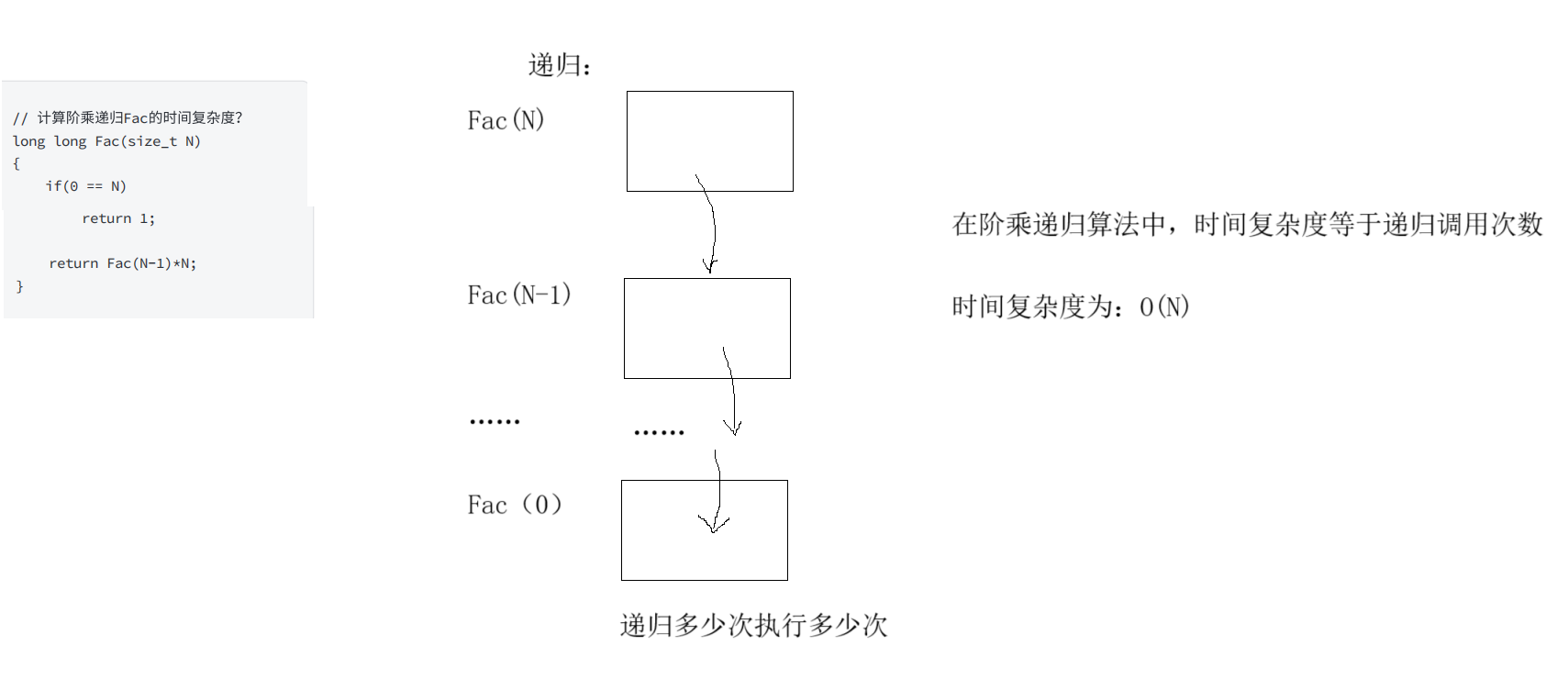
数据结构——时间复杂度
1.数据结构有关知识
1.1数据结构
数据结构是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。没有一种单一的数据结构对所有用途都有用,所以有各种各样的数据结构,例如:线性表、图、哈希等等。
1.2算法
算法就是一系列的计算步骤,用来将输入的数据转化成输出结果。
数据结构和算法不分家。
2.算法效率
衡量一个算法好坏的标准是什么?
让我们看看一道题:

本题的大概思路就是这样子的:

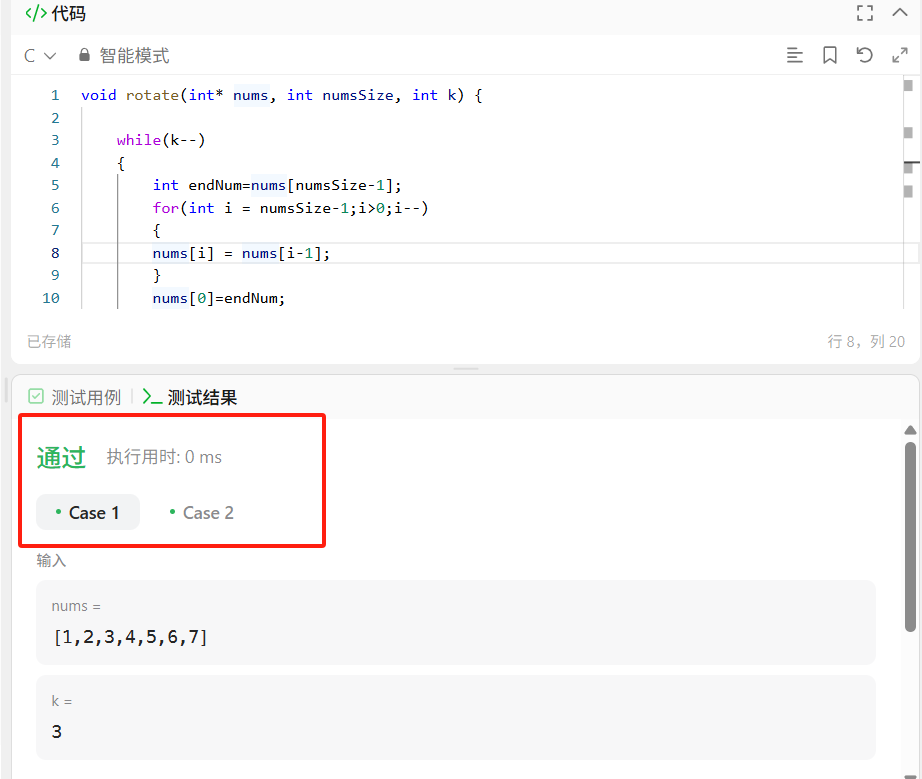
点击运行,显示通过,但是当我们点击提交时,就出现了“超过时间限制的问题”,这又是为什么呢?
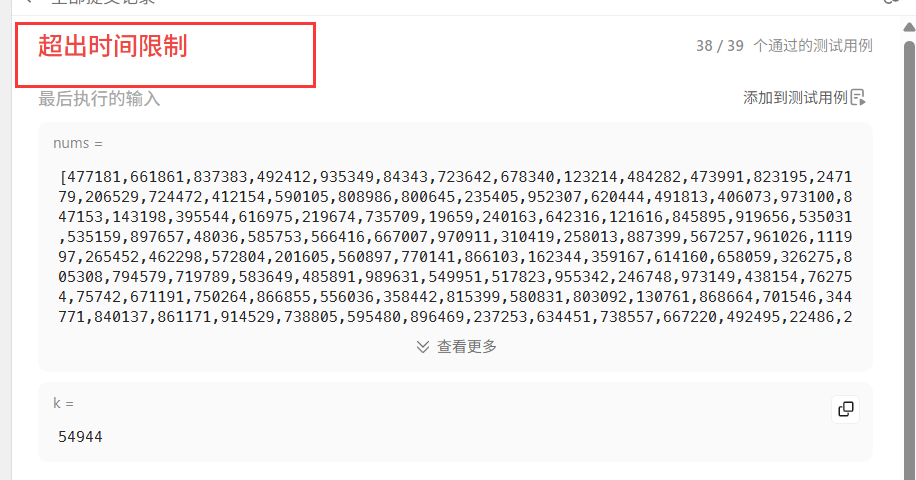 这就涉及到我们的复杂度的知识点了,衡量代码的好与坏一般是从时间和空间的两个维度去衡量的,即时间复杂度和空间复杂度。时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
这就涉及到我们的复杂度的知识点了,衡量代码的好与坏一般是从时间和空间的两个维度去衡量的,即时间复杂度和空间复杂度。时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。
3.时间复杂度
时间复杂度:在计算机科学中,算法的时间复杂度是一个函数式T(N),定量的描述了该算法的运行时间。时间复杂度是衡量程序的时间效率,为什么不用程序运行的时间来衡量呢?
观察以下代码:
int main()
{int start= clock();for (int i = 0; i < 100000; i++){for (int j = 0; j < 100000; j++){int a = 1;}}int end = clock();printf("%d\n", end - start);return 0;
}第一次运行结果:

第二次运行结果:

可以发现同一台电脑上面的两次运行的结果完全是不一样的。
- 程序运行的时间和编译的环境以及运行机器的配置有关,例如上面的例子。
- 同一个算法程序,用一个老低配置机器和新高配置机器,运行的机器也是不一样的。
- 并且如果想用时间来作为衡量标准的话,不能再写程序之前就判断出,只能通过程序写好之后去测试。
所以我们不可以使用时间来作为衡量的标准。
影响时间复杂度的条件有:每条语句的执行时间*每条语句的执行次数
每条语句的执行时间都是一样的,所以我们忽略,就以每条语句的执行次数来作为标准。
代码1:

上面的代码中总共执行 ++count 有 (n^2+2n+11) 次,但是最后的时间复杂度却是:O(n^2)
这又是因为什么呢?
是因为大O阶规则:
- 时间复杂度函数式T(N)中,只保留最高阶项,去掉那些低阶项,因为当N不断变大时, 低阶项对结果影响越来越小,当N无穷大时,就可以忽略不计了。
- 如果最⾼阶项存在且不是1,则去除这个项⽬的常数系数,因为当N不断变大,这个系数对结果影响越来越小,当N无穷大时,就可以忽略不计了。(去除常数系数是因为影响时间复杂度的是输入的条件)
- T(N)中如果没有N相关的项目,只有常数项,⽤常数1取代所有加法常数。(这里的1代表的是常数项而不是常数1)
代码2:

根据大O阶规则的第一、二项得出代码2的时间复杂度为:O(N)
代码 3:


代码4:
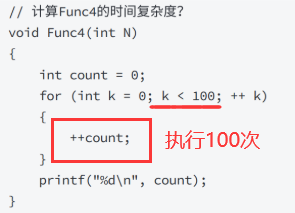

代码3的时间复杂度为:O(1) 这里的1代表的是时间复杂度为常数次数而不是1次,无论常数是多少,对时间的增长趋势是没有任何影响的。
代码5:
// 计算strchr的时间复杂度?
const char * strchr ( const char* str, int character)
{
const char* p_begin = s;
while (*p_begin != character)
{
if (*p_begin == '\0')
return NULL;
p_begin++;
}
return p_begin;
}

总结:
我们会发现有些算法的时间复杂度存在最好、最坏、平均的情况。
最坏情况:最大的运行次数(上界)
最好情况:最小的运行次数
平均情况:期望的运行次数(下界)
大O的渐进表示法在实际中一般关注的是最坏的情况,也就是算法的上界。
代码6:(冒泡排序)


代码7:

 时间复杂度:
时间复杂度:
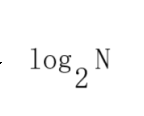
代码8: