周志华《机器学习导论》第11章 特征选择与稀疏学习
目录
1. 子集搜索与评价（怎么选特征子集 好子集的指标）
2. 过滤式选择 + Relief（不管学习器 先筛一下）
3. 包裹式选择 + LVW（为学习器量身定做）
4. 嵌入式选择与L1正则化（边筛边训 正则化）
5. 稀疏表示与字典学习（特征提取 最好的特征与最好的字典）
6. 压缩感知（把压缩过的信号 稀疏表示后 恢复出原信号）
k限定等距性RIP
应用：书籍推荐问题
1. 子集搜索与评价（怎么选特征子集 好子集的指标）
维度灾难 选择与当前学习任务比较相关的特征 进行训练
冗余特征：比如已知立方体的长宽高 底面积就是冗余特征 可以由其他特征得到
但可能会降低学习任务的难度 比如用表面积和高 能够更好的学习体积
如何选择特征子集，评价特征子集的好坏？
贪心式的双端“子集搜索” 从空集开始加 加入后使得总体效果最好的特征；也可以删最无关的特征
“子集评价”评估特征对分类的帮助 用信息增益 可参考决策树那部分
下文将阐释三种特征选择方法
2. 过滤式选择 + Relief（不管学习器 先筛一下）
先对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关
Relief (Relevant Features) 二分类问题 对每个特征计算相关统计量 选择值最大的几个
先在其同类样本中寻找最近邻xi,nh，称为“猜中近邻”
再在其异类样本中寻找最近邻xi,nm，称为“猜错近邻” 对于样本xi,属性j
猜错间距-猜中间距 代表j 在样本区分的帮助性 然后再对i个样本进行求和
多分类问题变形为Relief-F； 多种类 对每个类找猜错近邻 再按种类样本数目放缩权重
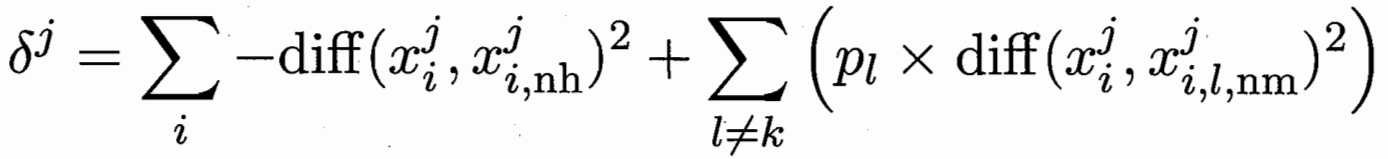
3. 包裹式选择 + LVW（为学习器量身定做）
针对给定学习器选择最有利于其性能、 “量身定做”的特征子集
（1）随机产生特征子集
（2）使用交叉验证 如果性能更好（误差小 或者误差同特征数少）则替换为最优解
（3）如果连续T次没有更新答案 就退出循环
与过滤式相比 最终学习器的性能更好； 但因为需多次训练学习器 计算开销会大很多
4. 嵌入式选择与L1正则化（边筛边训 正则化）
特征选择过程与学习器训练过程同时完成
正则化项： L2范数岭回归； L1范数LASSO 更易于获得“稀疏”(sparse)解 w非零变量少
L1正则化问题的求解可使用近端梯度下降（PGD）迭代求解
如果先不考虑正则化系数 仅有f(x)
所以进行的迭代为
如果加上正则化系数 最小化目标为
因为每个分量独立 可解得
5. 稀疏表示与字典学习（特征提取 最好的特征与最好的字典）
若把数据集看做一个矩阵 每一行代表一个样本 每一列代表一个特征 特征选择即选择列
稀疏表示可以去除无关列 降低学习难度与计算开销 提高模型的解释性。
字典学习的目标：提取事物/任务 最本质的特征（类似于字典当中的字或词语）
就像话语是通过字词的排列组合 可以用这个字典里的特征表示这一类的所有事物
字典好不好：取决提取的特征是否稀疏 是否为任务的本质特征
进行反复迭代 （1）先固定字典B 求到每个x 最好的α表示；
（2）再固定α求最好的字典B。 反复这两步。
字典d维度=任务样本x的维度 k维度为存了多少基本的字/词 特征；可以通过控制k控制字典大小。
6. 压缩感知（把压缩过的信号 稀疏表示后 恢复出原信号）
对模拟信号采样得数字信号 信息传递时又需压缩数字信号，目标可精确重构原信号
假定有长度为m的离散信号x，采样得长度为n的采样后信号y, 使用测量矩阵φ 短了很多n<<m
正过来得到压缩后的值很容易
如何实现已知y 反推x？
有难度 因为从信息少的返回信息多的 可能对应很多信息多的解（欠定方程）
若有
则
若根据y能恢复出稀疏的s 再用s恢复x
压缩感知：先获得原信号的稀疏表示； 再利用稀疏性,从少量观测样本中恢复原信号
k限定等距性RIP
找到合适的矩阵A 恢复s 条件y=As Min= s的零范数（非零元素个数）
L1 范数最小化在一定条件下与L0 范数最小化问题共解 所以可以转化为LASSO形式
应用：书籍推荐问题
假设获得一些读者对于书的评价
没有书被所有人度过 也没有人读过所有书 所以相当于很多值是缺失的 需要恢复出完全的值
压缩感知技术恢复欠采样信号的前提条件之一是 信号有稀疏表示
书籍的特征有 题材、作者等 题材数远小于书本数 所以满足稀疏性
矩阵补全问题 可写成找一个秩最小的矩阵X 并且矩阵X对应位置与A有效值位置数相同
转化为最小化 核范数（奇异值之和）