考研数学微分学（第一讲）

一.函数的概念和特性

1.判断单值函数和有没有反函数的方法

铅直划线定单、多（单值函数还是多值函数），水平划线定反、直（判断是否有反函数，前提是单值函数）

2.具体函数例子

                           

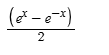
3.函数的四种特性

(1)有界性

定义：若存在常数 M>0，使得函数 f(x) 在定义域内的所有值满足 ∣f(x)∣≤M，则称 f(x) 为 ​有界函数。

• ​分类：
  • ​上界：存在 M 使 f(x)≤M；
  • ​下界：存在 m 使 f(x)≥m；
  • ​无界函数：不存在这样的 M 或 m。

(2)单调性

定义：若函数 f(x) 在区间 I 上，对任意 x1​<x2​：

• ​单调递增：f(x1​)≤f(x2​)；
• ​严格单调递增：f(x1​)<f(x2​)；
• ​单调递减：f(x1​)≥f(x2​)；
• ​严格单调递减：f(x1​)>f(x2​)。

判定方法：

• 导数符号法：
  • f′(x)≥0 ⇒ 单调递增；
  • f′(x)≤0 ⇒ 单调递减。

(3)奇偶性

定义：

• ​奇函数：f(−x)=−f(x)，图像关于原点对称；
• ​