信号与系统-风中醉风
绪论
信号与系统:从时域、频域、离散,研究信号
输入信号->系统->输出信号
时域不好分析->转换到频域->时域
第一章-信号与系统基础
信号的表达方式
1.表达式
2.波形
数形结合百般好 ——华罗庚
信号的分类
1.确定信号 随机信号(不研究)
确定信号:能够写出表达式
2.连续信号 离散信号
连续变量:自变量定义范围内,除去不连续点,对于任意自变量可以得到确定的函数值。
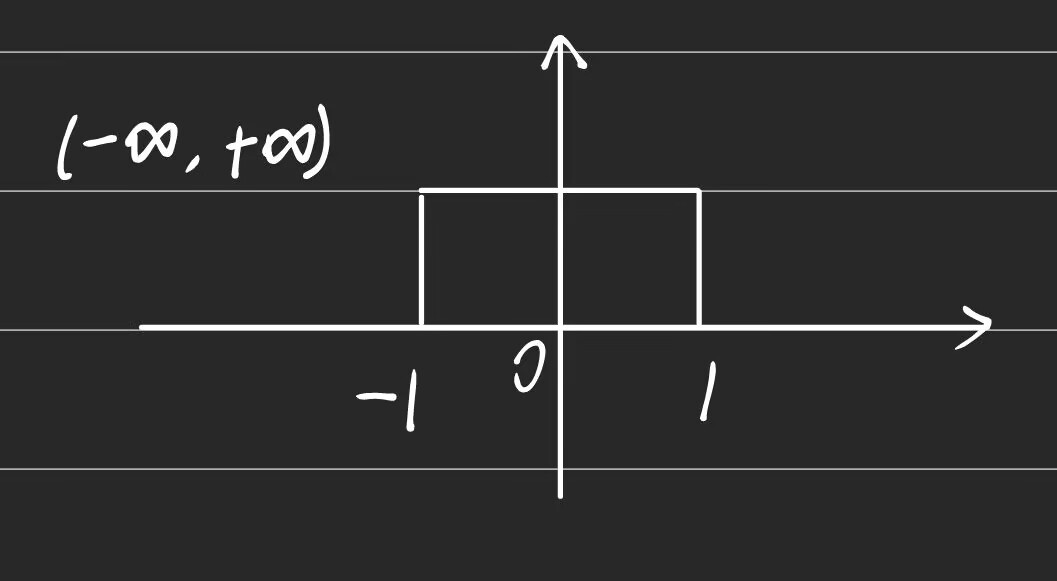
除去不连续点 -1 , 1,其余点仍然满足连续信号条件。
离散信号:也称序列,只研究 n = 0,±1,±2,±3…(量化/取整)
3.模拟信号 数字信号
模拟信号:自变量和信号参量取值都连续
数字信号:自变量和信号参量取值都离散
4.周期信号 非周期信号
周期信号 :
(1)连续信号:f (t) = f (t+mT) , m = 0,±1,±2…
(2)离散信号:f (n) = f (n+mN) , m = 0,±1,±2… N为整数
结论 对于一个周期为T的信号 f (t),离散化后得到 f (βn) 的周期为:
1.当 T/β 为无理数,此时 f (βn) 无周期
2.当 T/β 为有理数 = b/a ,有周期为12
结论

T1,T2 无最小公倍数–周期商为无理数,和差商积无周期
5.实信号 复信号
复数:a+jb Ae(j角度)

6.奇信号 偶信号
f (t) = f (-t) 偶信号
f (t) = -f (-t) 奇信号
任意一个信号,都可以拆成奇分量和偶分量

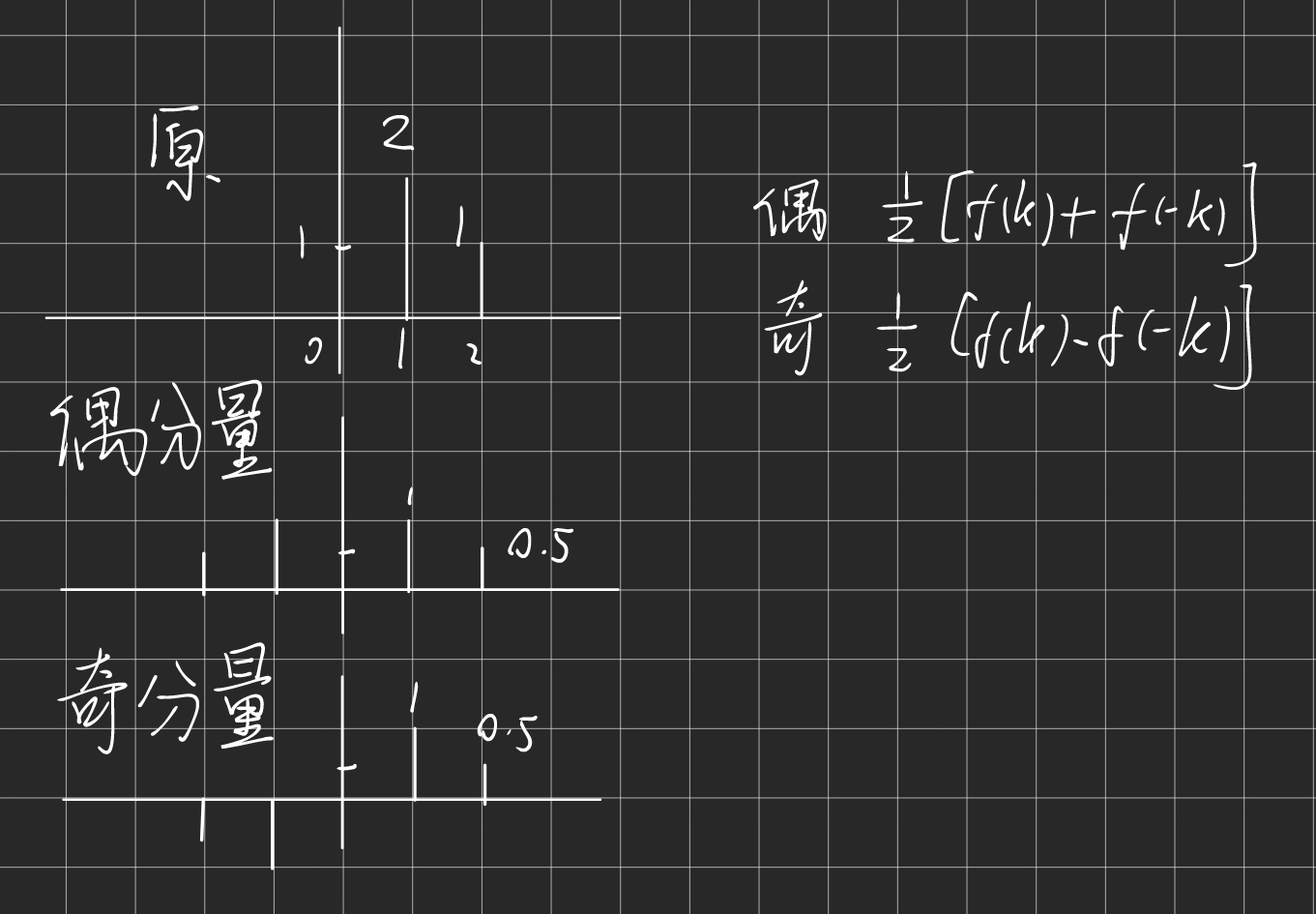
7.能量信号 功率信号
连续:

离散:连续是积分,离散是求和

能量有限:能量信号,功率为0
功率有限:功率信号,能量无穷
非能量非功率信号:能量无穷,功率无穷。
结论可积信号,若是时限的,则f (t) 是能量信号。
可积条件下,周期信号一定是功率信号。
信号的运算
1.相加
离散:各个点相加
连续:表达式相加
2.相乘

3.微分,积分
连续信号
微分:表达式求导

积分:变上限积分,上限为 t (积分后函数值连续)

f (t) 求导 d f(t)/dt 变上限积分-> != f (t),不一定等于f (t),负无穷为0,可以还原
先变上限积分,再求导还原,得到原 f (t)

离散信号
微分->差分
积分->累加

4.翻折
f (t) -> f (-t)
f (k) -> f (-k)
5.移位
f (t) -> f (t - t0) 左加右减
6.尺度变换
连续:
f (t) -> f (at) (a>0)
a > 1 压缩
0<a<1 扩展
离散:
压缩:删去非整数点
扩展:新的点为0,删除非整数点
有限序列表示 f (n) = { 3,1,1,2,2,1,3 },0点位置标注
所有的变换都是针对 t 而言
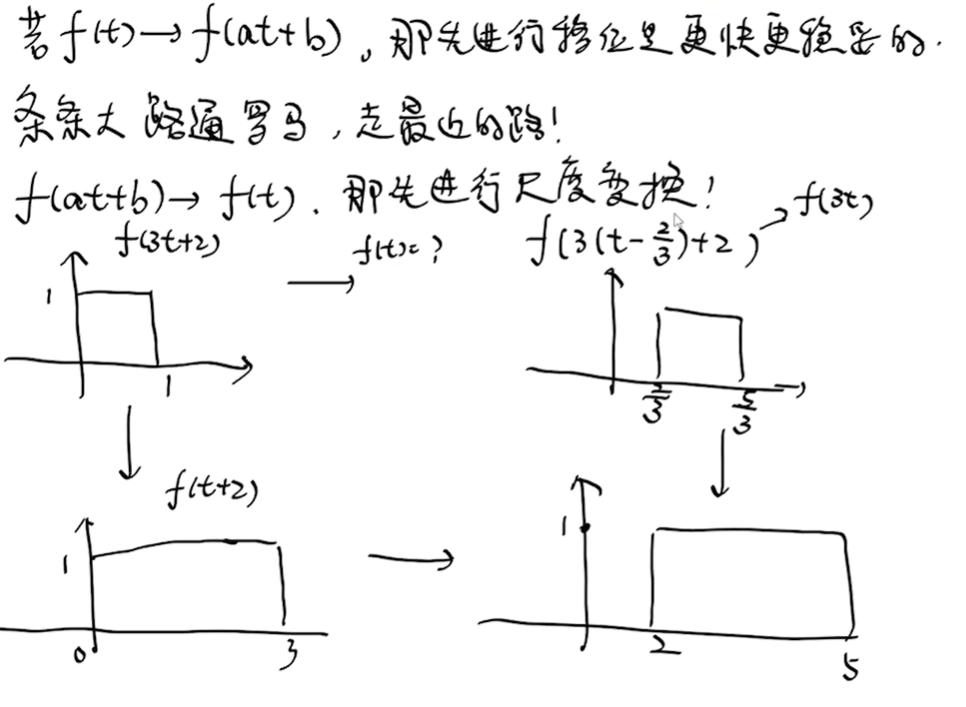
t -> at+b

at+b -> t
常见信号
1.指数信号
单边衰减指数信号:

2.正弦信号
单边衰减正弦信号

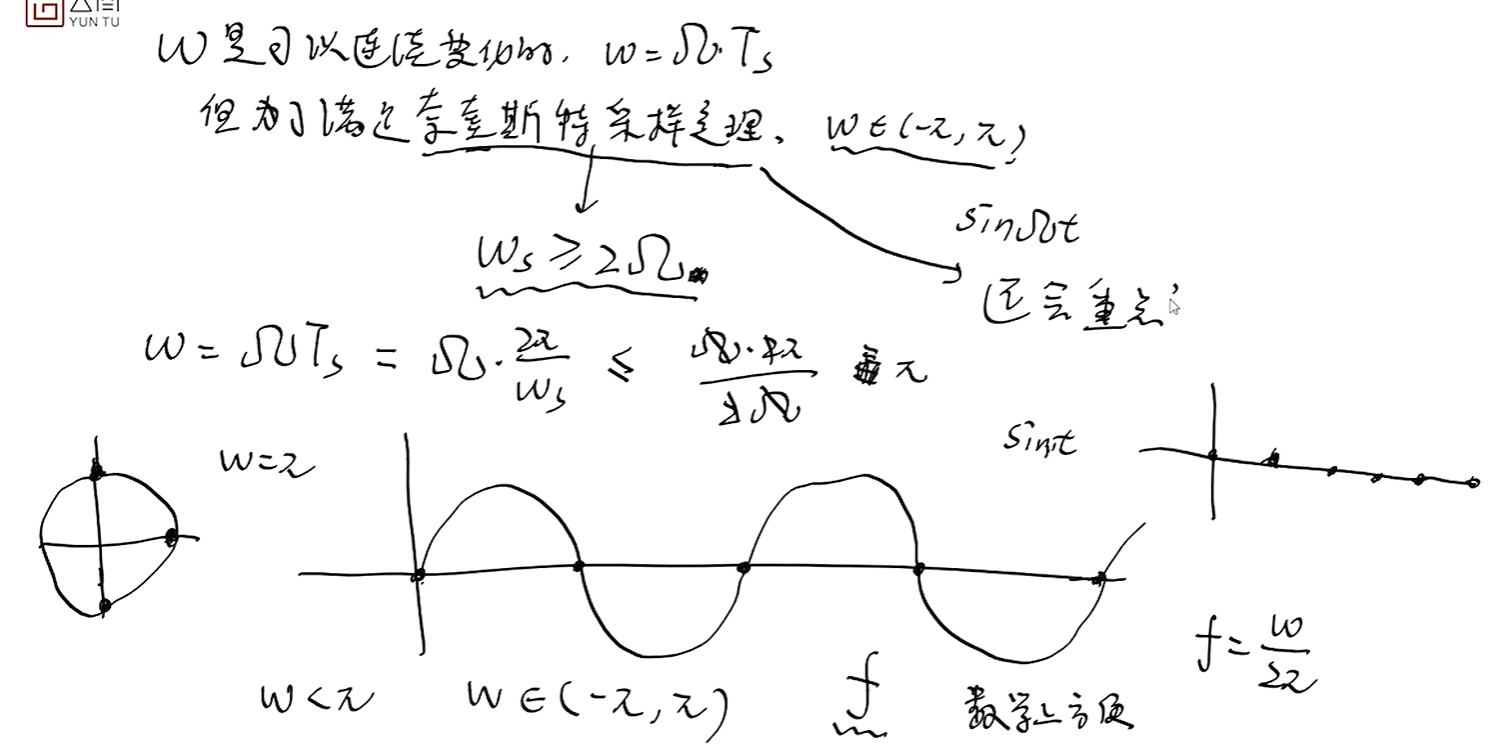
采样(暂时了解,后续重点讲)
欧拉公式:


3.复指数信号 (没听懂,不知道有什么用 4.26)

4.Sa信号 (抽样函数)
理想抽样:采点
显示抽样:矩形脉冲
震荡,t增大,总体减小
sin t = 0,Sa(t) = 0
5.常数信号
一般是功率信号
一个信号的功率等于直流功率与交流功率之和
6.斜变信号
奇异信号:


7.阶跃信号

窗口

门函数

u(t)的定义域是全实数
一个信号的多种表示

阶跃序列

8.符号函数

9.冲激信号
冲激信号的导数是冲激偶信号
性质:
抽样性质


积分变为阶跃信号

2到-2积分,符号提出去,上下限互换,积分为-1

拆分的方法

冲激信号的尺度变换

综合题

冲激信号是偶信号
冲激信号可以用来表示任意信号
单位脉冲序列

冲激偶信号
求导:斜边->阶跃->冲激->冲激偶
不连续点是阶跃信号

冲击偶信号的积分性质

系统的特性
1.线性系统
性质:输入为0,输出为0

判断是否为线性
线性

非线性
带常熟

带高次方

2.时不变性
线性+时不变性 == 线性时不变系统 LTI系统
系统特性不随时间变化而变化

时变

所有变化针对t而言

上:先经过系统,再延时:所有 t 都延时 t0,
下:先延时,经过系统,其他t,不会延时
经过系统就是,对运算操作。
先经过系统再时移
先时移再经过系统 二者相等,则是时不变
3.因果系统
输出只取决于现在和过去的输入有关,而与将来无关

无记忆性,一定是因果:取决于当前
记忆性:取决于当前和之前
4.稳定系统
稳定性:若输入有界,则输出有界
5.可逆系统
可逆性:一个输入对应一个输出

6.离散系统
把 t 换成 n
错题:
线性时不变连续系统的数学模型是常系数线性微分方程 ,而常系数线性差分方程是线性时不变离散系统的数学模型


第二章—时域分析法
物理意义强,易理解
1.零输入响应 零状态响应
响应:输出;激励:输入
输出取决于 输入(外部激励)+系统初始状态(内部激励)
零输入响应:输入信号为零,仅由初始状态响应 rzi,yzi
零状态响应:初始状态为零,仅由输入引起的响应 rzs,yzs
线性系统:全状态 = 零状态+零输入

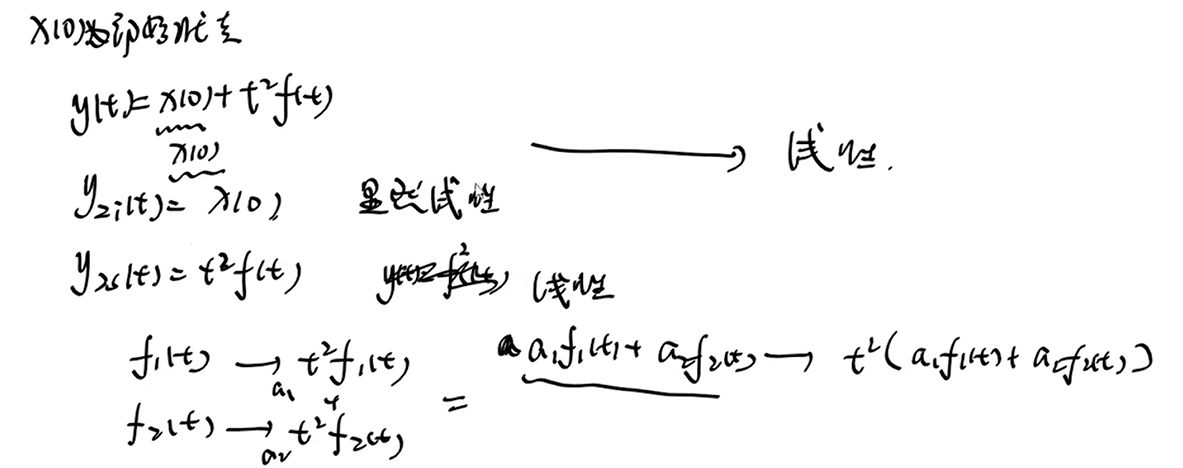
分量拆分,判断为两个线性分量

常系数线性微分方程/差分方程一般形式


判断 线性,时不变
线性:假设满足线性,看是否满足等式

时不变:假设f (t-t0) 输出y0(t),发现与t - > t-t0式子吻合

卷积
卷积表示一个输入信号经过系统如何得到输出的过程
卷积:积累,当前和过去的输入对现在的输出有影响,当前的输入影响着现在和未来的输出
LTI系统下定义


h (t) 单位冲激响应:单位冲激信号δ(t)作用下的零状态响应
u(n)->LTI->g(t)单位阶跃响应

LTI系统的微分性,积分性

卷积->积分形式
求解卷积举例:
连续

离散

卷积的图解
简单函数左移t,翻着,从左往右滑动,分情况相乘积分,注意积分变量是 涛 不是t

结论

卷积的性质
1.交换律

积分从左往右和从右往左积差个负号,求和都一样

简单信号复杂变换
2.分配律
两个系统相互卷积——串联

两个系统相加——并联
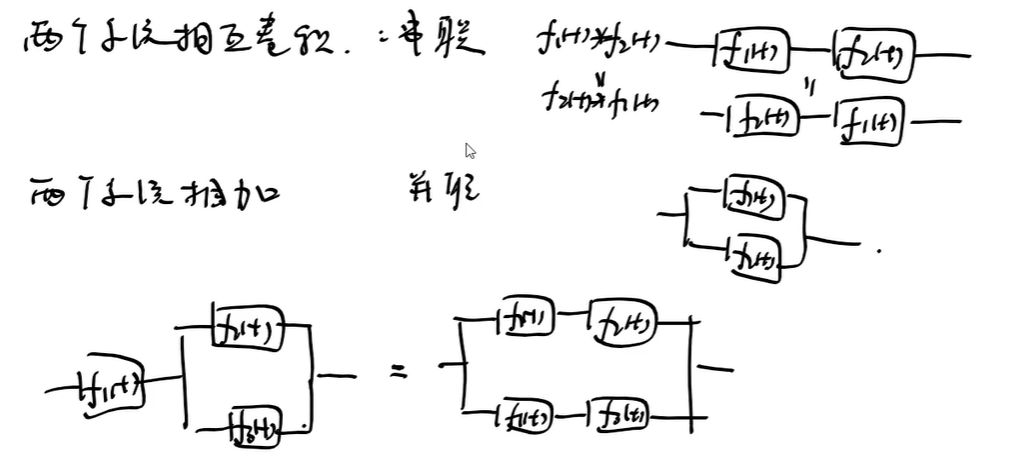
常数可以提到卷积前面

3.结合律

既有乘积也有卷积,结合律不能用

奇异信号的卷积


一阶导

k阶导同理


卷积的时移

结合律+时移性质

卷积存在:
1.都有始或都有终
2.其中一个是时限的,有始有终
卷积的微积分特性
上标正是求导,负是积分

使用条件被求导的函数,t=负无穷=0,或被积分的函数本身的净面积为0
卷积的尺度变换

有限长序列的卷积
对位相乘求和法,不进位乘法

找零点

边界0有用就写,没用就省略

两矩形卷积
等腰梯形:
左端点a+c,右端点b+d
d-c是短底


与常数卷积

一些卷积积分



卷积和



微分方程和差分方程
线性常系数
微分方程的建立
电路图->微分方程 (非重点)
框图->微分方程
求和,倍乘,积分,微分
通过加法器来列式子

差分方程的建立

微分方程的求解
1.等号右端为0,求通解;
2.根据e(t)的形式,得到特解;
3.根据初始条件,解出待定系数;

冲激函数匹配法?
零状态响应和零输入响应的求解
1.零输入响应的求解:

输入为0,求通解即可
2.零状态响应
初始状态为0

强迫响应与自由响应

瞬态响应与稳态响应

