当前位置：首页 > ds >正文

电机控制(三)-电机控制方法基础

ds 2025/9/5 15:01:56

电机控制

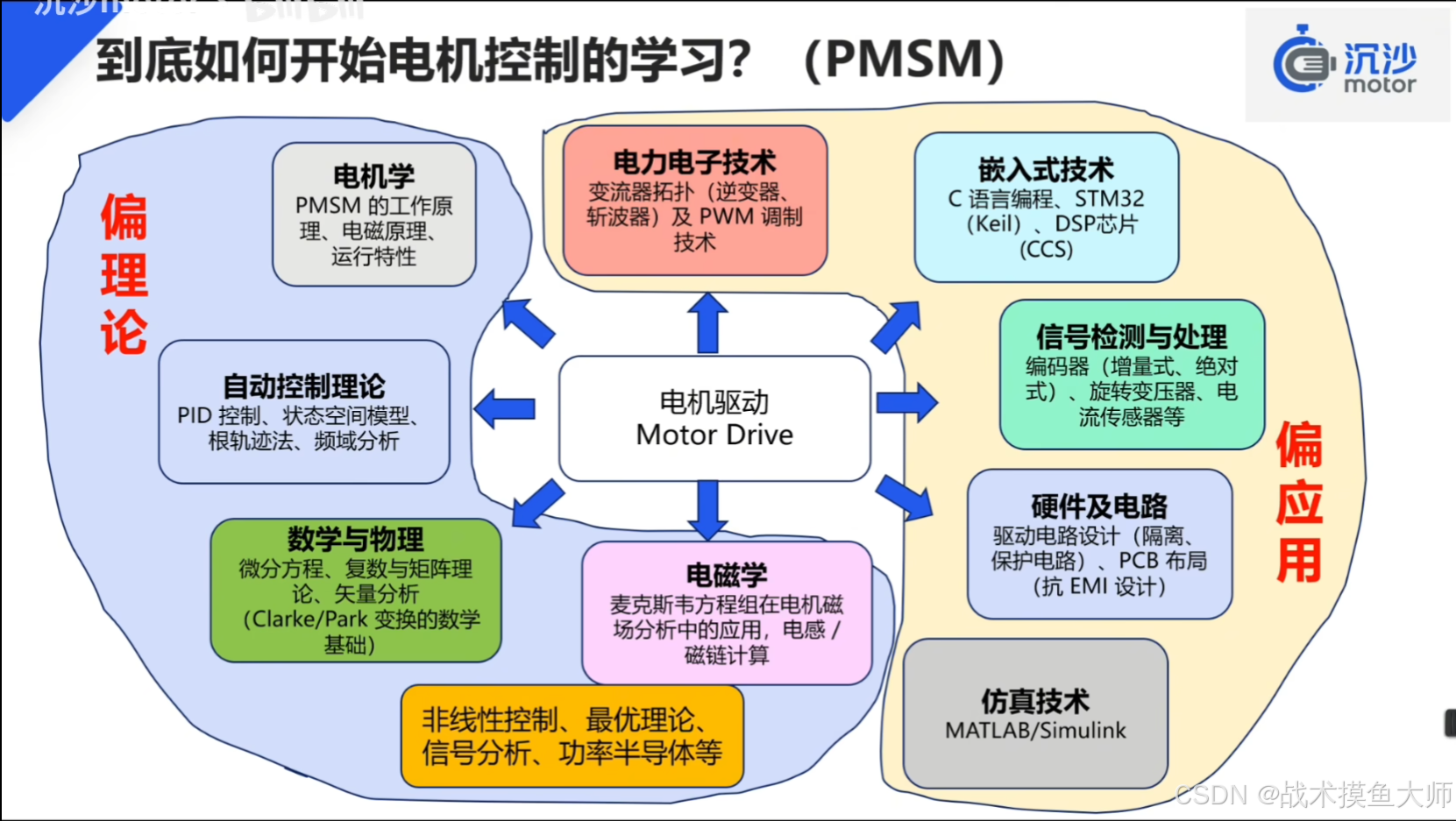
在这里插入图片描述

图片来自B站up主沉沙motor，视频连接

电机控制是运动控制的一部分，运动控制又是控制中的一大分支。

从宏观的角度看，控制领域分为三大分支：过程控制，运动控制，离散控制(逻辑控制)。这三者覆盖了 90% 以上的工业控制场景，是理解控制领域的 “骨架”。三大分支的本质区别，在于控制对象的 “状态特性” 不同—— 是 “连续变化的物理量”（如温度、压力）、“精确的机械运动”（如转速、位置），还是 “离散的逻辑状态”（如开关、工序步骤）。
其中，运动控制的核心是 “精确控制机械部件的运动状态”，控制对象是电机、执行机构等运动部件，参数包括 “位置、速度、加速度、力矩”，目标是 “高精度、高动态响应、高稳定性”，比如让电机从 0 转速快速加速到 1000rpm 且无超调，或让机械臂精准定位到 ±0.01mm。
以机器人为例，根据控制的层次，机器人的运动控制可以分为指令层，轨迹层，运动执行层（电机控制）

运动控制是自动化领域的核心技术，核心目标是通过控制电机的运动状态（位置、速度、加速度、转矩），驱动机械系统（如机器人、机床、传送带）按预期轨迹或规律运动。其技术链条可简化为：目标指令→轨迹规划→电机控制算法→驱动执行→反馈修正，其中电机控制算法是连接“指令”与“执行”的核心桥梁，直接决定运动精度、动态响应和稳定性。

运动控制的基本框架

理解电机控制算法前，需先明确运动控制的整体逻辑，算法在其中的定位如下：

指令层：用户输入目标（如“机械臂末端移动到坐标(10,20,30)”“传送带速度保持5m/s”）；
轨迹规划层：将目标指令分解为连续、平滑的中间轨迹（如S型加减速曲线），避免机械冲击；
控制算法层：根据轨迹规划结果和反馈信号（位置、速度、电流），计算电机的控制量（电压、电流、脉冲）；
驱动层：将控制算法输出的信号转换为电机可识别的驱动信号（如PWM波、脉冲序列）；
反馈层：通过传感器（编码器、霍尔、电流传感器）实时采集电机状态，回传给控制算法层，形成闭环。

其中，电机控制算法是闭环控制的“大脑”，负责根据“目标与实际的偏差”计算最优控制量，是决定运动性能的核心。

核心电机控制算法

电机控制算法的分类可按“是否依赖反馈”（开环/闭环）和“控制对象”（位置/速度/电流）划分，以下是最常用的几类算法：

1. 开环控制算法

开环控制无需反馈，直接按预设规则输出控制量，适合低成本、低精度场景：

脉冲控制（步进电机专属）：
原理：通过控制器输出脉冲序列，每1个脉冲对应电机固定步距角（如1.8°/脉冲），脉冲频率决定转速。
特点：结构简单（仅需脉冲发生器），但无修正能力，负载过大或速度突变时易“失步”。
应用：3D打印机、低端数控机床。

2. 闭环控制算法

闭环控制通过反馈信号计算偏差，动态修正控制量，是高精度运动控制的主流，核心算法包括：

PID控制

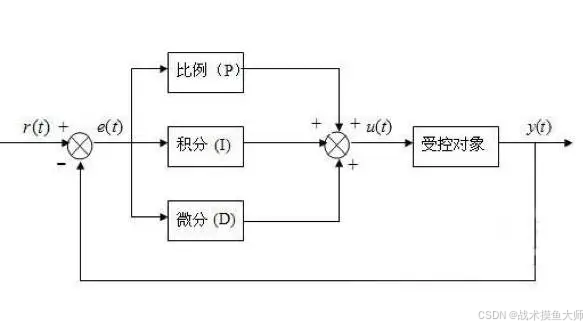
在这里插入图片描述

PID（比例-积分-微分）是所有闭环控制的“基石”，通过三个环节协同修正偏差：

比例（P）：按“当前偏差”输出控制量（偏差越大，控制量越大），快速响应偏差，但可能存在稳态误差；
积分（I）：按“偏差累积量”输出控制量，消除稳态误差（如电机负载变化导致的速度偏移）；
微分（D）：按“偏差变化率”输出控制量，抑制超调（如电机启动时的冲量）。

在电机控制中的分层应用（三环PID级联）：

电流环（最内环）：最快响应（带宽最高），控制电机绕组电流，抑制电流波动（如负载突变时的电流冲击）；
速度环（中环）：通过调节电流环给定，稳定电机转速（如指令速度500rpm，实际480rpm时，增加电流提升转速）；
位置环（最外环）：通过调节速度环给定，控制机械位置（如目标位置100mm，实际95mm时，提升速度指令补全位置）。

特点：结构简单、易实现，适合大多数工业场景（如伺服电机、变频调速）；但对非线性负载（如摩擦、惯性变化）适应性弱。

实际控制中多用PI控制，很少使用微分反馈，微分环节对 “误差变化率” 极度敏感 —— 即使是微小的噪声波动（变化率大），也会被 D 环节放大，导致控制器输出剧烈波动：D 环节的 “超前调节” 仅在 “大惯性、慢响应” 系统中有价值（如温度控制、液位控制），对于电机的速度环，电流环这种响应本身极快的系统反而会导致 “过度反应”。
而且PID 控制器需额外整定K_d（微分系数），但K_d的参数窗口极窄：

K_d过小：微分作用不明显，无法体现 PID 优势；
K_d过大：会过度放大噪声，导致系统不稳定；

更关键的是，K_d对电机参数变化（如负载惯量变化、摩擦系数变化）非常敏感 —— 参数微小变化就可能导致微分作用失配，而工业场景中电机负载（如机床切削负载、风机负载）往往是动态变化的，PID 的鲁棒性远不如 PI。

矢量控制（FOC，磁场定向控制）：交流电机的“解耦神器”

针对交流电机（如PMSM、BLDC、异步电机）的强耦合特性（电流与转矩、磁通相互影响），FOC通过坐标变换实现“转矩与磁通的独立控制”，让交流电机像直流电机一样易于调控：

核心步骤：
1. Clark变换：将三相电流（ABC轴）转换为两相静止电流（αβ轴），简化计算；
2. Park变换：将αβ轴电流转换为与转子同步旋转的两相电流（dq轴），其中：
  - d轴电流（Id）：控制磁通（类似直流电机的励磁电流）；
  - q轴电流（Iq）：控制转矩（类似直流电机的电枢电流）；
3. 对Id和Iq分别进行PID闭环控制（通常Id=0以减少损耗），再通过“Park逆变换”和“SVPWM”转换为三相电压，驱动电机。

特点：转矩控制精确、动态响应快（响应时间＜10ms）、效率高，是永磁同步电机（PMSM）和高端直流无刷电机（BLDC）的标配算法；但需高精度位置反馈（编码器）和复杂的坐标变换计算。

直接转矩控制（DTC）

直接转矩控制（Direct Torque Control，DTC）是继矢量控制（FOC）之后发展起来的另一种高性能交流电机控制策略，其核心特点是 “直接以转矩和磁链为控制目标，无需复杂的坐标变换”，尤其在动态响应速度上具有显著优势。
DTC与FOC目标一致（解耦控制），但路径不同：不依赖坐标变换，直接通过“电压空间矢量”控制电机的转矩和磁链：

核心逻辑：
1. 实时估算电机的实际转矩和磁链（基于电流、电压和电机参数）；
2. 对比“目标转矩/磁链”与“实际值”，通过开关表直接选择最优电压矢量（逆变器的开关状态），快速修正偏差。

特点：动态响应比FOC更快（适合快速启停场景），算法简单（无复杂变换）；但低速时转矩脉动大，精度略低于FOC。
应用：电梯曳引机、注塑机等对响应速度要求高的场景。

模型预测控制（在电机控制中不常用）

MPC是一种先进控制算法，通过“建立电机数学模型”预测未来状态，再优化控制量使未来偏差最小：，在电机控制中不常用，更多用在机器人轨迹规划。

核心步骤：
1. 基于电机参数（电阻、电感、磁链）建立状态方程（描述电流、速度、位置的关系）；
2. 预测未来N个时刻的电机状态（如未来5ms的速度）；
3. 求解优化问题（如最小化“预测状态与目标状态的误差”），输出当前最优控制量；
4. 滚动优化（每控制周期重复上述步骤，适应参数变化）。

特点：能处理非线性、多约束（如电流限幅、速度限幅）场景，抗干扰能力强；但计算量大，需高性能处理器（如DSP、FPGA）。
应用：新能源汽车驱动、高精度伺服系统。

典型电机控制框架

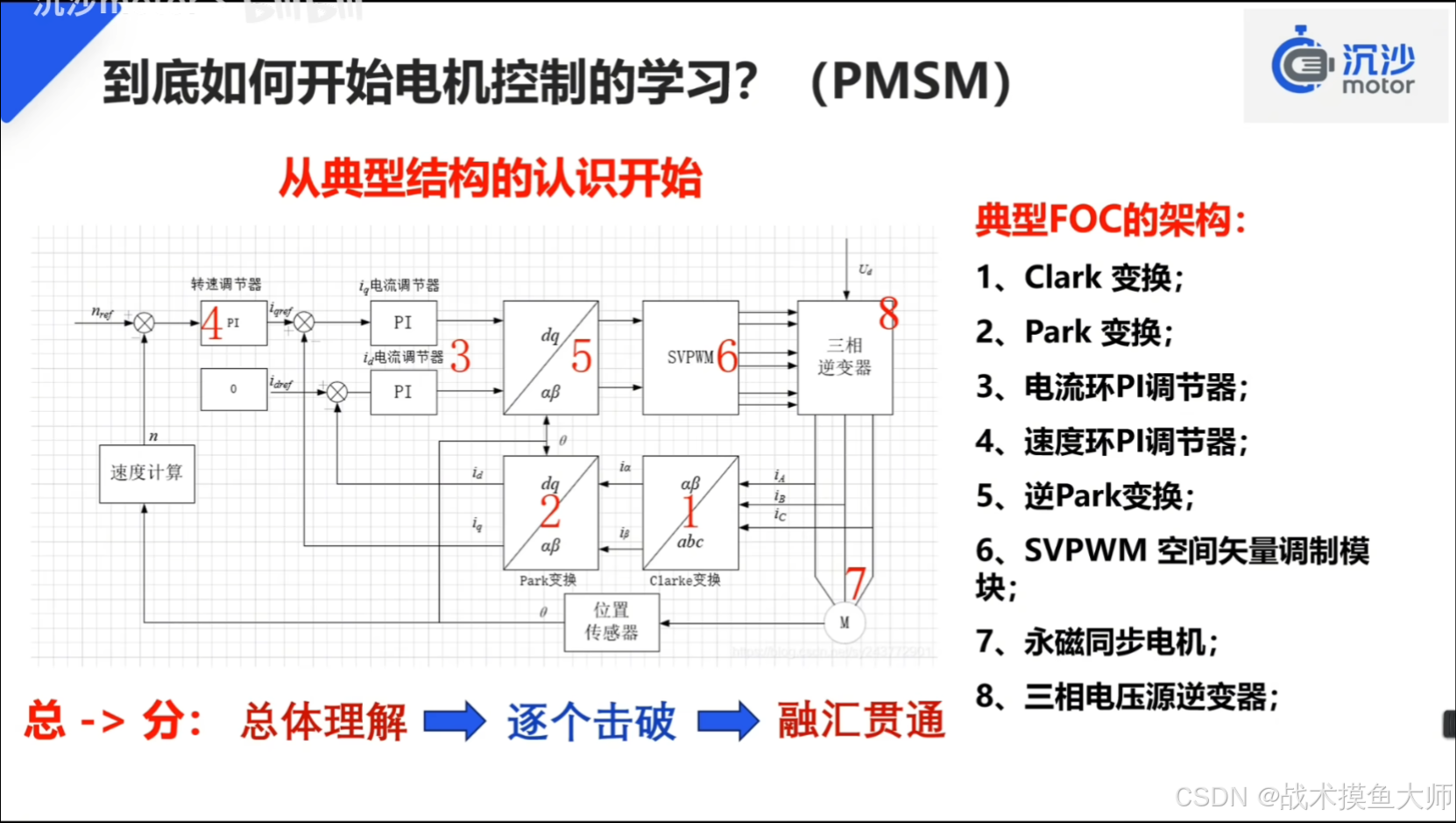
在这里插入图片描述
这张图里体现了典型的电机控制框架，系统的输入为目标速度，控制对象为最下角的电机M。
具体流程为：

控制回路

PI速度环控制器：控制速度，输入为目标转速，输出为q轴目标电流(q轴目标电流与转矩直接相关，所以输出也可以看作是目标转矩)。
电流环控制器：使用PI分别控制q轴和d轴的电流，输入为目标电流，输出为dq轴的参考电压
- d轴的参考电流跟电机的类型有关，对于外贴式PMSM电机， $i_{dref}=0$ 。
- 这里的参考电流到参考电压的转换，只是控制信号的数值转换，不是真的出现了电流与电压的转换，下面的交流直流参考电压转换也是一样。
逆Park变换：通过逆Park变换将dq轴参考电压转换为 $αβ\alpha \beta$ 轴参考电压
- dq轴参考电压是直流的，即一直不变的。 $αβ\alpha \beta$ 轴参考电压是交流的，即随时间不断变化的。这里的交流/直流只是是数学上的等效变化，并不是真的电压发生了交流和直流的变化。
逆Clarke变换：在逆Park变换与SVPWM间还有一个逆Clarke变换，将 $αβ\alpha \beta$ 轴参考电压转换为三相参考电压
SVPWM调制器：根据参考电压生成三相逆变器开关信号，控制 IGBT 等功率器件的通断。
- SVPWM相比传统 PWM，能更高效利用直流母线电压（电压利用率高）、减少电流谐波，从而提升电机效率、降低发热，改善动态性能。
三相逆变器：根据 SVPWM 的开关信号，将直流母线电压逆变为三相交流电压，供给电机定子绕组。输入为直流母线和SVPWM开关信号
- 直流母线电压可以直接来自直流电源，也可以来自交流电网然后经过整流得到的直流电压，220V的单相电整流完得到310V直流电压。380V三相电整流完得到540V直流电压

观测/反馈回路

观测也好，反馈也好，前馈也好，其实都是一样的，都是反馈/前馈中的一部分。

三相电流采集：采集电机的三相定子电流 $i_a、i_b、i_c$ （来自逆变器输出或电流传感器）。
Clarke变换：将三相电流从「abc三相静止坐标系」转换为「αβ两相静止坐标系」的电流 $iα、iβi_\alpha、i_\beta$ 。
- 三相系统数学模型复杂（存在耦合、交流分量），转换为两相静止坐标系后，维度降低、模型简化，便于后续处理。
Park变换：结合位置传感器提供的转子位置角 $θ\theta$ ，将 $iα、iβi_\alpha、i_\beta$ 从「αβ两相静止坐标系」转换为「dq两相旋转坐标系」的电流 $i_d、i_q$ 。
- dq坐标系是与转子同步旋转的坐标系（若为永磁同步电机，dq轴与转子磁极同步；若为异步电机，与转子磁场同步）。
- 旋转后，原本交流的电流分量 $iα、iβi_\alpha、i_\beta$ 会变成直流分量 $i_d、i_q$ （若控制理想），从而将“强耦合的交流系统”转化为“解耦的直流子系统”，方便用PI控制器调节。

不同电机类型与控制算法的匹配

电机类型的特性决定了算法选择，两者需“性格匹配”：

电机类型	核心控制算法	选择原因
步进电机	开环脉冲控制	无需反馈，结构简单，匹配其“按脉冲步进”的特性；高端场景可加编码器实现闭环PID修正（闭环步进）。
直流无刷电机（BLDC）	六步换相（基础）、简化FOC（高端）	基础应用用六步换相（霍尔传感器+方波电流），低成本；高端需平滑控制时用FOC（正弦波电流）。
永磁同步电机（PMSM）	矢量控制（FOC）	正弦波反电动势需匹配正弦波电流，FOC的dq轴解耦能最大化其高精度、高动态特性。
异步无刷电机	矢量控制（基于转子磁场定向）、V/F控制	简单调速用V/F控制（开环，电压与频率成正比）；高精度场景用矢量控制（解耦励磁与转矩电流）。

算法性能的核心评价指标

判断电机控制算法的优劣，需关注以下指标：

动态响应：从“指令变化”到“实际跟随”的时间（如速度从0→1000rpm的响应时间，FOC通常＜50ms）；
稳态精度：稳定运行时的偏差（如位置精度±0.01mm，速度波动±0.1%）；
抗扰能力：负载突变时的恢复能力（如负载增加50%，速度恢复到目标值的时间）；
鲁棒性：电机参数变化（如温度导致电阻变化）时的性能稳定性（MPC＞PID）。

总结

从开环到闭环，从简单PID到智能MPC，电机控制算法的演进始终围绕一个核心目标：在“精度、速度、稳定性”之间找到最优平衡。实际应用中，没有“最好”的算法，只有“最适合”的算法——低成本场景用PID或开环控制，高精度场景用FOC，快速响应场景用DTC，复杂非线性场景用MPC。理解算法的原理和特性，才能根据需求选择最优方案。