生存分析入门教程

本篇文章The Complete Introduction to Survival Analysis in Python适合对生存分析感兴趣的新手，亮点在于详细介绍了生存分析的基本概念、应用场景以及如何在Python中实现相关算法。该方法适用于需要预测事件发生时间的场景，如员工流失、设备维护、客户支付等。例如，通过生存分析，企业可以在员工流失前采取措施，提高员工留存率。

同类型文章：

• 译|生存分析Survival Analysis案例入门讲解（一）
• 译|生存分析Survival Analysis案例入门讲解（二）
• 生存分析——KM生存曲线、hazard比例、PH假定检验、非比例风险模型（分层/时变/参数模型）（二）

---

---

1 什么是生存分析？

生存分析是统计学的一个分支，它衡量直到某个事件发生为止的预期时间长度。这个名称来源于临床研究，我们字面上关心的是患者的生存，换句话说，是延长直到死亡的时间长度。

根据其应用领域，生存分析可以有许多不同的名称。在工程学中，我们称之为 可靠性分析，在经济学中称之为 持续时间分析。事件发生时间分析也是一个常见的名称。

1.1 回归还是分类？

考虑到生存分析衡量的是事件发生所需的时间长度，这意味着它是一种回归类型。

然而，生存分析的输出并不是一个连续的数字。

相反，我们的目标是生成生存函数或风险函数。

生存函数表示事件在时间函数中不发生的概率。

或者，风险函数表示事件在某个时间点发生的概率。

当我们实现不同的生存分析模型时，我们将更详细地了解这些函数。

1.2 何时使用生存分析？

既然我们了解了生存分析衡量的是事件发生所需的时间，我们就可以看到它并非医疗保健领域的专属。

事实上，只要我们需要在事件发生 之前 采取行动，就可以使用生存分析。

以员工流失问题为例。假设我们有以下数据集。

Salary	Years employed	Nb. of promotions	Direct manager	Has left
75000	2	1	John Doe	0
105000	4	2	Jane Doe	0
40000	2	0	John Doe	1

直观地，我们将其视为一个二元分类问题，即员工要么留在公司，要么离开。

如果我们的模型预测员工会留下，他们会留下多久？如果模型预测员工会离开，他们会在多久之后离开？作为一个分类问题，我们要么不知道这些问题的答案，要么需要一个固定的时间段。例如，我们的数据被标记为员工在 6 个月内离职。

将员工流失视为一个生存分析问题，我们就可以将员工留在公司的概率表示为时间的函数。这样，我们就可以在员工实际离职之前采取行动。此外，我们可以分析我们的特征，并确定每个特征如何影响员工留下的时间长度。

现在，这只是一个例子，但生存分析可以应用于更多情况，例如：

• 设备需要维护之前需要多长时间？
• 客户偿还债务之前需要多长时间？
• 软件 bug 解决之前需要多长时间？
• 客户进行下一次购买之前需要多长时间？

核心信息是，当我们不仅对事件的发生感兴趣，而且对事件发生之前的时间长度感兴趣时，就应该使用生存分析。

2 生存分析中的数据

由于生存分析关注事件的发生以及事件发生之前的时间长度，因此我们的数据必须包含这些信息。

让我们回顾一下我们关于员工流失的示例数据集。

Salary	Years employed	Nb. of promotions	Direct manager	Has left
75000	2	1	John Doe	0
105000	4	2	Jane Doe	0
40000	2	0	John Doe	1

在这里，我们可以看到我们拥有生存分析所需的信息：我们有雇佣年限以及员工是否离职。

当然，我们也有关于尚未离职的员工的数据。

这就是我们所说的删失数据。对于两名员工，我们不知道他们何时会离开公司，或者他们是否会离开。

尽管如此，我们不会等到所有员工都离开才采取行动，因此生存分析专门设计用于处理删失数据。

2.1 删失数据的类型

删失数据有三种类型：

1. 右删失
2. 左删失
3. 区间删失

让我们来看看每种类型。

2.1.1 右删失数据

对于右删失数据，我们知道每个受试者的起始点，但我们没有观察到每个人的事件，如下所示。

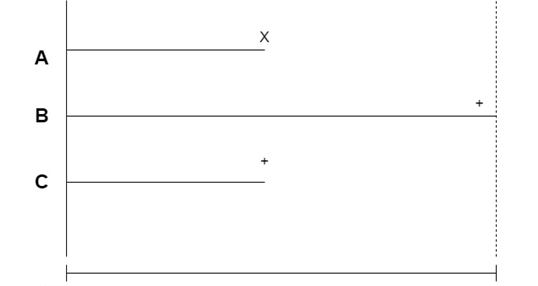
右删失数据：我们知道起始点，但不知道事件是否发生在每个受试者身上。图片由作者提供。

在上图中，受试者 A 离开了公司。对于受试者 B，在实验期间，他们留在了公司。但我们无法知道他们之后是否离开了。因此，它是右删失的。

受试者 C 是右删失数据的另一个例子，有人只是离开了实验。这可能发生在临床试验场景中，当有人还活着，但离开了试验，所以我们失去了他们的踪迹。

2.1.2 左删失数据

为了理解左删失数据，让我们考虑感染病毒的例子。

在这里，左删失数据意味着我们不知道这个人何时被感染，但我们知道他们感染了病毒。

左删失数据：我们不知道事件何时发生，但我们稍后观察到它。图片由作者提供。

在上图中，事件在我们观察到之前就发生了，但我们无法知道确切的时间。尽管如此，这种类型的数据仍可用于生存分析。

2.2 区间删失数据

最后，区间删失数据是指事件发生在两个观察时刻之间，但我们不确定具体何时发生。

区间删失数据：事件发生在两个观察点之间。图片由作者提供。

为了理解这一点，假设你去看医生并进行病毒检测。在你的第一次就诊时，结果是阴性，你没有被感染。

然后，下周你再次去看医生并进行病毒检测。现在，检测结果是阳性，这意味着你在两次就诊之间的某个时间被感染了，但我们不确定具体何时。

3 应用生存分析

现在我们对生存分析、其应用以及它可以处理的数据类型有了全面的了解，让我们通过一个例子来实际应用生存分析。

在这里，我们使用 1980 年的退伍军人管理局肺癌试验数据集（Kalbfleisch, J.D., Prentice, R.L.: “The Statistical Analysis of Failure Time Data.” John Wiley & Sons, Inc. (2002)）。该数据集可公开下载。

该数据集包含 137 名患者的数据，具有变量并且是右删失的。这意味着在研究期间，并非所有患者都去世了。

这里，这个实验有两个主要目标：

1. 不同的治疗方法能否改善生存时间？
2. 我们能否预测患者的生存时间？

为了回答第一个问题，让我们实现我们的第一个生存分析方法：Kaplan-Meier 估计器。

3.1 实现 Kaplan-Meier 估计器

Kaplan-Meier 估计器是一种非参数统计方法，用于估计生存函数，它非常适用于右删失数据。

正如我们很快将看到的，Kaplan-Meier 估计器将生成一个由一系列下降的水平阶梯（像楼梯一样）表示的生存函数。给定足够的样本，该函数将逼近真实的生存函数。

Kaplan-Meier 估计器的主要假设是，删失数据与未删失数据具有相同的生存概率。因此，如果有人离开了实验，我们将假设他们与留在实验中并被我们观察到的受试者具有相同的生存概率。

为了实现它，我们将使用 scikit-survival Python 包。这是一个附带数据集和常见生存分析模型的库。

首先，让我们读取数据。

from sksurv.datasets import load_veterans_lung_cancerX, y = load_veterans_lung_cancer()

太棒了！现在，我们可以导入 Kaplan-Meier 估计器并生成生存曲线。为此，我们需要传入两个参数：患者的状态（已故或未故）和事件发生的时间（从研究开始到观察经过了多少天）。

from sksurv.nonparametric import kaplan_meier_estimatortime, survival_prob = kaplan_meier_estimator(y['Status'], y['Survival_in_days'])

然后，我们可以绘制生存函数。

fig, ax = plt.subplots()  
ax.step(time, survival_prob, where='post')  
ax.set_ylabel('Probability of survival')  
ax.set_xlabel('Time')plt.tight_layout()

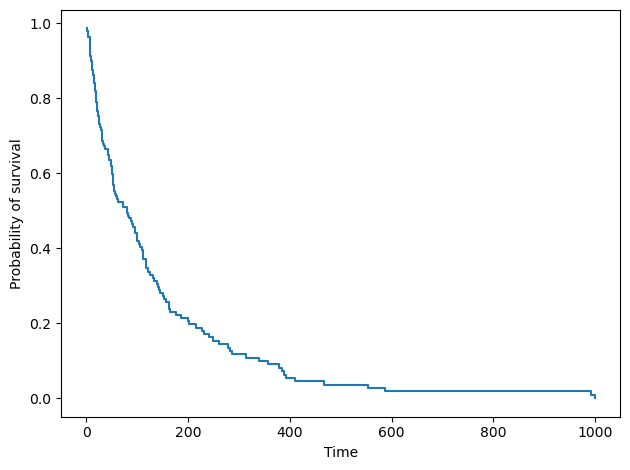
从上图可以看出，生存函数确实如预期般是一系列下降的水平阶梯。研究开始时，大多数患者都活着，因此生存概率很高。然后，曲线迅速下降，这意味着大多数患者在研究的前 400 天内去世。

现在，可以为不同组的患者生成生存函数。例如，在数据集中，施用了两种不同的治疗方法。看看其中一种治疗方法是否增加了生存机会会很有趣。

让我们亲自看看！我们根据治疗类型将数据分成两组，并生成生存函数。然后，我们绘制它。

for treatment_type in ('standard', 'test'):  mask_treatment = X['Treatment'] == treatment_typetime, survival_prob = kaplan_meier_estimator(  y['Status'][mask_treatment],  y['Survival_in_days'][mask_treatment]  )plt.step(time, survival_prob, where='post', label=f'{treatment_type}')plt.ylabel('Probability of survival')  
plt.xlabel('Time')  
plt.legend(loc='best')  
plt.tight_layout()

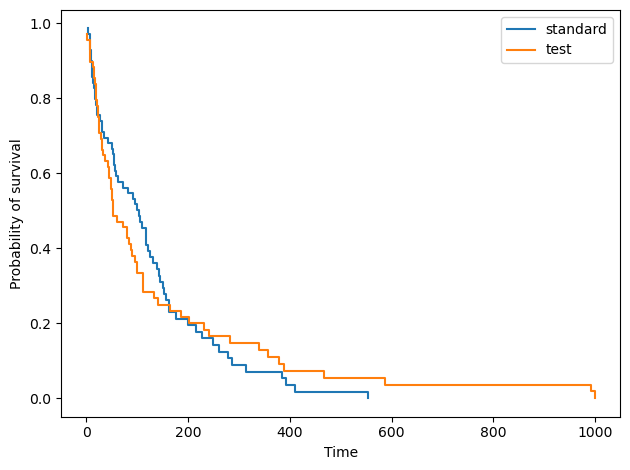
从上图来看，实验性治疗似乎比标准治疗产生了更持久的生存曲线。

但这种差异是否显著呢？

为了回答这个问题，我们使用对数秩检验（logrank test）。这是一种统计检验，用于确定两条生存曲线是否显著不同。在这里，零假设表明两条曲线没有显著差异。

使用 scikit-survival，我们可以运行测试并输出 p 值。

from sksurv.compare import compare_survivalgroup_indicator = X.loc[:, 'Treatment']  
groups = group_indicator.unique()chi2, pvalue = compare_survival(y, group_indicator)print(pvalue)

这会输出一个 0.93 的 p 值。由于它不小于 0.05，我们未能拒绝零假设，并得出结论，生存曲线没有显著差异。因此，治疗类型并没有帮助患者活得更久。

3.2 带有协变量的生存分析

Kaplan-Meier 估计器是一个很好的起点，但因为它是一个非参数模型，它无法考虑我们数据集中的任何特征。因此，我们将注意力转向可以考虑特征来估计生存函数的模型。

首先，让我们对数据进行独热编码，以便可以使用这些特征。

from sksurv.preprocessing import OneHotEncoderX_num = OneHotEncoder().fit_transform(X)

太棒了！现在，我们可以应用一个考虑协变量来评估生存的模型。在这里，我们使用 Cox 比例风险模型。

3.3 Cox 比例风险模型

Cox 比例风险模型是评估不同因素对生存影响的模型之一。通过这种方式，我们可以确定哪些因素可以改善生存，哪些因素会降低生存机会。

在这里，模型实际上估计的是风险函数。换句话说，它计算事件在某个时间点发生的概率。这与生存函数相反，生存函数估计事件在某个时间点不发生的概率。

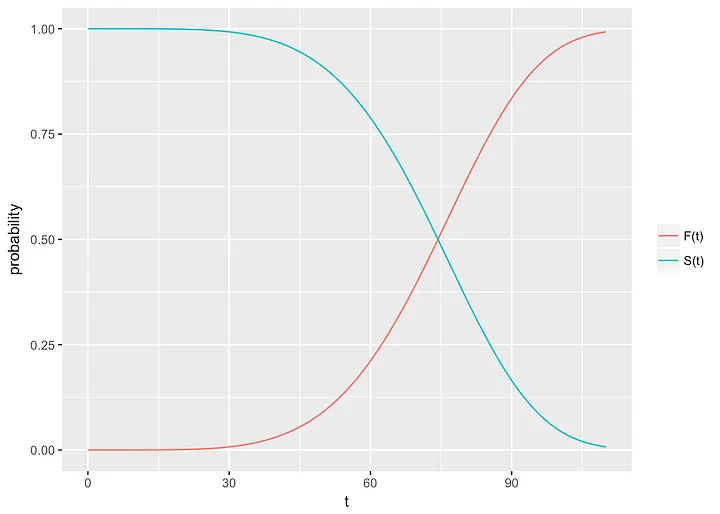
从上图可以看出，生存函数随时间递减，而风险函数随时间递增。当然，一旦我们有了其中一个函数，我们就可以很容易地计算出另一个。

因此，Cox 模型是一个表示为以下形式的风险函数：

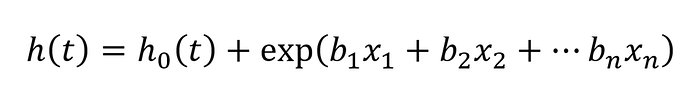
这里，h 表示风险（事件发生的概率），协变量由 x 表示。然后，系数 b 可以用来解释每个协变量的影响：

• 如果 b = 0，则该特征没有影响
• 如果 b > 0，则该特征增加风险（因此生存率降低）
• 如果 b < 0，则该特征降低风险（因此生存率增加）

该模型的一个重要假设是风险是成比例的，并且该比例与时间无关。因此，如果受试者 A 在初始时间点的死亡风险是受试者 B 的两倍，那么无论我们在时间上的哪个位置，该比例都保持不变。

3.4 应用 Cox 比例风险模型

现在我们了解了 Cox 模型，让我们将其应用于我们的数据集。

我们只需初始化模型并将其拟合到我们的数据中。

from sksurv.linear_model import CoxPHSurvivalAnalysisestimator = CoxPHSurvivalAnalysis()  
estimator.fit(X_num, y)

然后，给定未见患者的数据，模型可以为每个患者生成生存函数。请注意使用 predict_survival_function 方法来获取生存函数，而不是风险函数。

X_test = pd.DataFrame.from_dict({  1: [65, 0, 0, 1, 60, 1, 0, 1],  2: [65, 0, 0, 1, 60, 1, 0, 0],  3: [65, 0, 1, 0, 60, 1, 0, 0],  4: [65, 0, 1, 0, 60, 1, 0, 1]},  columns=X_num.columns, orient='index')pred_surv = estimator.predict_survival_function(X_test)time_points = np.arange(1, 1000)for i, surv_func in enumerate(pred_surv):  plt.step(time_points, surv_func(time_points), where='post', label=f'Sample {i+1}')plt.ylabel('Probability of survival')  
plt.xlabel('Time')  
plt.legend(loc='best')  
plt.tight_layout()

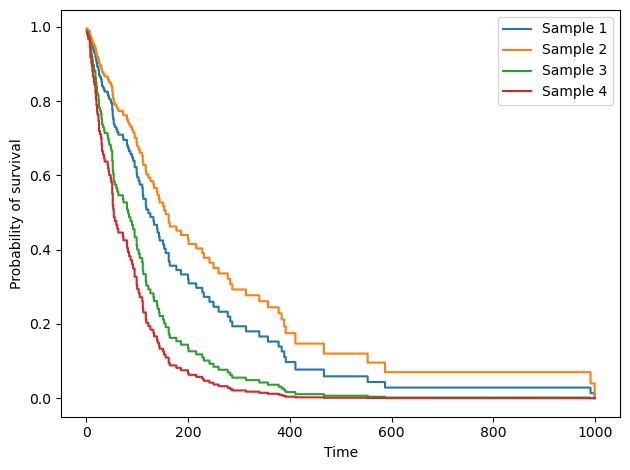
从上图可以看出，模型为每位患者生成了一个独特的生存函数。我们可以看到，样本 4 的生存率下降最快，而样本 2 的生存率下降最慢。

3.5 评估生存分析模型

那么，我们从 Cox 比例风险模型中得到了预测和生存曲线。但我们如何知道这些预测是否准确呢？

生存分析中常用的评估指标是**一致性指数（concordance index）**或 c-index，以及时间依赖性 ROC AUC。让我们更详细地探讨这两个指标。

3.5.1 一致性指数（c-index）

生存模型将预测一个风险概率。因此，具有较高风险概率的样本应该具有较短的生存时间。

然后，为了计算 c-index，我们取一对样本并寻找以下情况：

• 如果这对样本中的两个样本都被删失，则忽略这对样本（对 c-index 没有影响）
• 如果预测风险较高的样本的生存时间低于这对样本中的另一个样本，则这是一个一致对（c-index 增加）
• 如果预测风险较高的样本的生存时间长于这对样本中的另一个样本，则这对样本是不一致的（c-index 减少）。

然后，为了解释 c-index，我们使用与分类中的 ROC AUC 相同的逻辑：

• 0.5 是一个随机模型
• 1.0 是一个完美模型
• 0 是一个每次都预测错误的模型

因此，你希望你的 c-index 至少大于 0.5，并且越接近 1 越好。

3.5.2 使用 c-index 评估我们的 Cox 模型

现在，让我们计算 Cox 模型的 c-index。

from sksurv.metrics import concordance_index_censoredestimator.score(X_num, y)

这返回一个 0.74 的 c-index，这意味着我们的模型比随机模型表现更好，这是一个好兆头。

3.5.3 时间依赖性 ROC AUC

如果你曾处理过分类问题，你可能遇到过 ROC AUC 作为评估指标。你基本上通过测量 ROC 曲线下的面积来评估模型的性能。同样，你希望面积大于 0.5 并尽可能接近 1。

现在，在生存分析中，我们有一个连续的结果，这意味着 ROC 会随时间变化，这与二元分类不同。例如，客户可能按时支付信用卡，但在未来的某个时间点开始违约。

因此，使用时间依赖性 ROC AUC 对于评估模型预测事件在时间 t 之前发生的能力很有用。

3.5.4 使用动态 ROC AUC 评估我们的 Cox 模型

使用 scikit-survival，让我们使用时间依赖性 ROC AUC 评估我们的 Cox 模型。

from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X_num, y, test_size=0.2, stratify=y['Status'], random_state=42)cph = CoxPHSurvivalAnalysis()  
cph.fit(X_train, y_train)from sksurv.metrics import cumulative_dynamic_auctime_interval = np.arange(8, 184, 7)cph_risk_scores = cph.predict(X_test)  
cph_auc, cph_mean_auc = cumulative_dynamic_auc(y_train, y_test, cph_risk_scores, time_interval)fig, ax = plt.subplots()ax.plot(time_interval, cph_auc, marker='o')  
ax.axhline(cph_mean_auc, ls='--')  
ax.set_xlabel('Days after enrollment')  
ax.set_ylabel('Time-dependent AUC')plt.grid(True)  
plt.tight_layout()

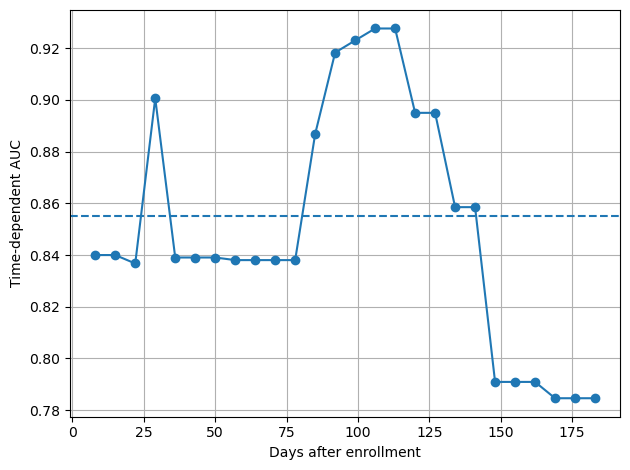
如上图所示，我们模型的性能随时间变化。我们看到其最高性能在 75 到 125 天之间。因此，我们的模型在中期预测效果最好。

从这里，我们可以开发其他生存模型，看看它们在短期或长期预测事件方面是否更好，以补充 Cox 模型。