数据结构八股
数据结构
1.10种排序算法汇总
*先谈一谈稳定性:稳定性简单来讲就是考虑排序后值相同的元素和排序前是否保持一致(如排序前a1和a2值相同,排序后仍是a1在前a2在后)*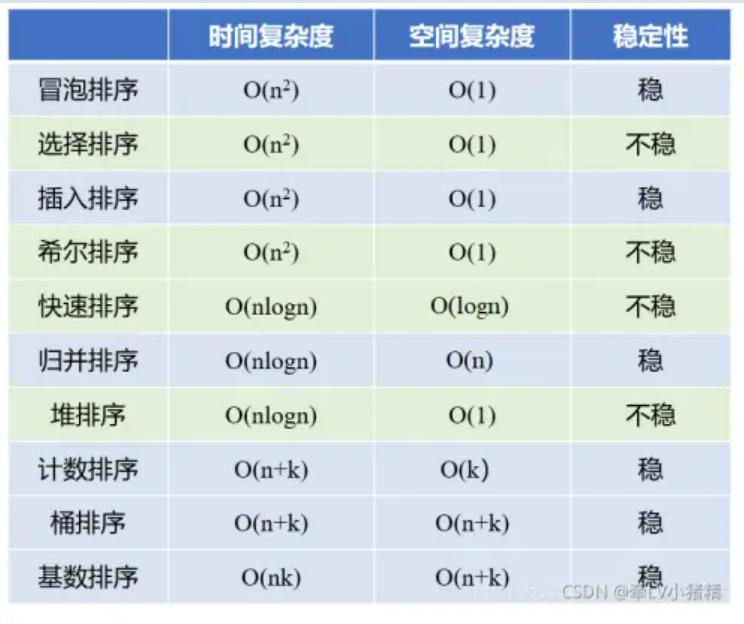
1.冒泡排序
通过对待排序序列从前向后(从下标较小的元素开始),依次**对相邻两个元素的值进行两两比较**,若发现**逆序则交换**,使值较大的元素逐渐从前移向后部,就如果水底下的气泡一样逐渐向上冒。
//定义一个标志位,用于判定元素之间是否进行了交换 boolean flag = false; for (int i = 0; i < arr.length - 1; i++) { for (int j = 0; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1]) { //进入这个if分支里边,则说明有元素进行了交换 //所以将flag=true flag = true; int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } //在进行完一轮的排序之后,判断本轮是否发生了元素之间的交换 //如果没有发生交换,说明数组已经是有序的了,则直接结束排序 if (!flag) { break; } else { //如果发生了交换,那么在下一轮排序之前将flag再次置为false //以便记录下一轮排序的时候是否会发生交换 flag = false; } }
2.选择排序
从数组中选择最小元素,将它与数组的第一个元素交换位置。再从数组剩下的元素中选择出最小的元素,将它与数组的第二个元素交换位置。不断进行这样的操作,直到将整个数组排序。
代码实现:
public void selectionSort(int[] arr) { if (arr == null) { return; } for (int i = 0; i < arr.length - 1; i++) { for (int j = i + 1; j < arr.length; j++) { if (arr[i] > arr[j]) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } } } }
3.插入排序
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
-
从第一个元素开始,该元素可以认为已经被排序;
-
取出下一个元素,在已经排序的元素序列中从后向前扫描;
-
如果该元素(已排序)大于新元素,将该元素移到下一位置;
-
重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
-
将新元素插入到该位置后;
-
重复步骤2~5。
插入排序的时间复杂度取决于数组的初始顺序,如果数组已经部分有序了,那么逆序较少,需要的交换次数也就较少,时间复杂度较低。
-
平均情况下插入排序需要 ~N2/4 比较以及 ~N2/4 次交换;
-
最坏的情况下需要 ~N2/2 比较以及 ~N2/2 次交换,最坏的情况是数组是倒序的;
-
最好的情况下需要 N-1 次比较和 0 次交换,最好的情况就是数组已经有序了。
代码实现:
public void insertSort(int[] arr) { if (arr == null) { return; } for (int i = 1; i < arr.length; i++) { int tmp